Completing the Square

Completing the Square is an algebraic method used to solve quadratic equations by transforming them into a perfect square trinomial. It is essential in understanding the relationship between rational and irrational numbers, as the process often reveals the nature of a quadratic equation’s roots. This technique involves manipulating integers, square and square roots to rewrite the equation in a simpler form, which aids in finding exact solutions. In statistics, it’s useful for least squares methods, providing insights into the numerical behavior of data. The method also helps in visualizing quadratic functions, revealing their minimum or maximum values.

What is Completing the Square?

Completing the Square is a method used to rewrite a quadratic equation of the form 𝑎𝑥²+𝑏𝑥+𝑐 = 0 into a perfect square form (𝑥−𝑝)² = 𝑞. This transformation makes it easier to solve for the roots of the equation by isolating 𝑥. The process involves adding and subtracting a specific value derived from the coefficient of 𝑥 to create a perfect square trinomial. Once in this form, the equation can be solved by taking the square root on both sides and then isolating 𝑥.

Completing the Square Method

Completing the Square is often used to factorize quadratic equations and identify their roots or zeros, especially when traditional factorization methods fail. A quadratic equation like 𝑎𝑥²+𝑏𝑥+𝑐=0 can sometimes be challenging to factor due to its complexity. In such cases, completing the square offers a viable solution.

Consider an example to understand this better:

If you have a quadratic equation that can’t be easily factorized, completing the square can rearrange it into a more manageable form. This approach involves rewriting 𝑎𝑥²+𝑏𝑥+𝑐 as a perfect square trinomial, making it easier to solve for 𝑥.

Completing the Square Steps

1. Standard Form: Start with a quadratic equation in standard form: 𝑎𝑥²+𝑏𝑥+𝑐 = 0.
2. Isolate 𝑥² and 𝑥: If 𝑎 (the coefficient of 𝑥²) is not 1, divide the entire equation by 𝑎a to make the coefficient of 𝑥² equal to 1.
3. Move 𝑐c: Move the constant term 𝑐c to the right side of the equation.
4. Find the Completing Term: Take half of the coefficient of 𝑥, 𝑏/2​, and then square it to get the completing term: (𝑏/2)².
5. Add and Subtract the Completing Term: Add this completing term to both sides of the equation to keep the equation balanced.
6. Form a Perfect Square: The left side of the equation can now be factored into a perfect square trinomial, (𝑥+𝑏/2)², which is equal to the right side.
7. Solve for 𝑥: Take the square root of both sides and solve for 𝑥. Remember to consider both the positive and negative square roots.
8. Simplify the Solution: Isolate 𝑥 to find the solution(s).

How to Apply Completing the Square Method?

Here’s an example with a different quadratic equation:

Example: Complete the square for 3𝑥²+12𝑥+9

Step 1:
Factor out the coefficient of 𝑥2x2, which is 33:
3𝑥²+12𝑥+9 = 3(𝑥²+4𝑥+3)
Now, the coefficient of 𝑥² is 1.

Step 2:
Find half of the coefficient of 𝑥x in the factored expression.
Here, the coefficient of 𝑥 is . Half of 4 is 2.

Step 3:
Square this number to find (4/2)² = 4.

Step 4:
Add and subtract 4 after the 𝑥 term inside the parentheses:
3(𝑥²+4𝑥+4−4+3)

Step 5:
Factorize the perfect square trinomial formed by the first three terms:
𝑥²+4𝑥+4 = (𝑥+2)²
So the expression becomes:
3((𝑥+2)²−4+3)

Step 6:
Simplify the constant terms:
−4+3 = −1
So, the final expression is:
3((𝑥+2)²−1) = 3(𝑥+2)²−3

This completes the square for the expression 3𝑥²+12𝑥+9 as:
3(𝑥+2)²−3

To summarize:

1. Ensure the coefficient of 𝑥² is 1.
2. Add and subtract (𝑏/2𝑎)² inside the parentheses.
3. Factorize the perfect square trinomial.
4. Simplify the expression to obtain the result.

Completing the Square Formula

The formula for completing the square simplifies the process of converting a quadratic equation into its vertex form. For a quadratic expression 𝑎𝑥²+𝑏𝑥+𝑐, we can rewrite it using the formula 𝑎(𝑥+𝑚)²+𝑛, where 𝑚 and 𝑛n are calculated as 𝑚 = 𝑏/2𝑎​ and 𝑛 = 𝑐−𝑏²/4𝑎​. This approach allows us to quickly identify the vertex of the parabola represented by the quadratic equation. By substituting the values of 𝑚m and 𝑛n back into the formula, we transform the equation into a format that highlights the parabola’s vertex. For example, given 2𝑥²+8𝑥+5, we find 𝑚 = 2 and 𝑛 = −3, which results in the equivalent form 2(𝑥+2)²−3. This method provides a streamlined way to manipulate quadratic expressions and understand their geometric properties.

Completing the Square Formula Examples

Example 1:

Given 3𝑥²+12𝑥+7

1. Calculate 𝑚:
   𝑚 = 12/2×3 = 12/6=2
2. Calculate 𝑛:
   𝑛 = 7−12²/4×3 = 7−144/12 = 7−12 = −5
3. Substitute into the Formula:
   Substitute 𝑚 and 𝑛 into the formula:
   3𝑥²+12𝑥+7 = 3(𝑥+2)²−5

Example 2:

Given −2𝑥²+4𝑥−1

1. Calculate 𝑚:
   𝑚 = 4/2×−2 = 4/−4 = −1
2. Calculate 𝑛
   𝑛 = −1−4²/4×−2 = −1−16/−8 = −1+2 = 1
3. Substitute into the Formula:
   Substitute 𝑚m and 𝑛 into the formula:
   −2𝑥²+4𝑥−1 = −2(𝑥−1)²+1

Derivation of Completing the Square Formula

To complete the square in the expression 𝑎𝑥²+𝑏𝑥+𝑐a, we follow these steps:

• Normalize the Coefficient of 𝑥2:
  Factor out 𝑎a to make the coefficient of 𝑥² equal to 1:
  𝑎𝑥²+𝑏𝑥+𝑐 = 𝑎[𝑥²+𝑏𝑎𝑥+𝑐𝑎]
• Analyze the First Two Terms:
  Consider the terms 𝑥² and (𝑏/𝑎)𝑥. The term 𝑥² represents the area of a square with side length 𝑥. The term (𝑏/𝑎)𝑥 represents the area of a rectangle with length 𝑏/𝑎​ and breadth 𝑥.
• Visualize the Problem Geometrically:
  Draw a square with side length 𝑥, giving it an area of 𝑥². Then, add a rectangle next to it with length 𝑏𝑎ab​ and breadth 𝑥, forming a new composite shape.
• Adjust the Rectangle into Two Identical Parts:
  The rectangle’s length 𝑏/𝑎​ can be split into two halves of 𝑏/2𝑎​ each. Attach these halves on either side of the original square to create a new shape.
• Create a New Larger Square:
  To complete the larger square, we need to fill in the missing square in the corner. The missing square’s side length is 𝑏/2𝑎​, and its area is (𝑏/2𝑎)² = 𝑏²/4𝑎²​.
• Add and Subtract the Missing Area:
  Add and subtract the missing area inside the factored expression: 𝑎[𝑥2+(𝑏/𝑎)𝑥+𝑏²/4𝑎²−𝑏²/4𝑎²+𝑐/𝑎]​
• Factor the Perfect Square Trinomial:
  The first three terms form a perfect square trinomial: 𝑎[(𝑥+𝑏/2𝑎)²−𝑏²/4𝑎²+𝑐/𝑎]
• Simplify the Expression:
  Simplify the expression further: 𝑎𝑥²+𝑏𝑥+𝑐 = 𝑎(𝑥+𝑏/2𝑎)²+𝑎(𝑐/𝑎−𝑏²/4𝑎²)

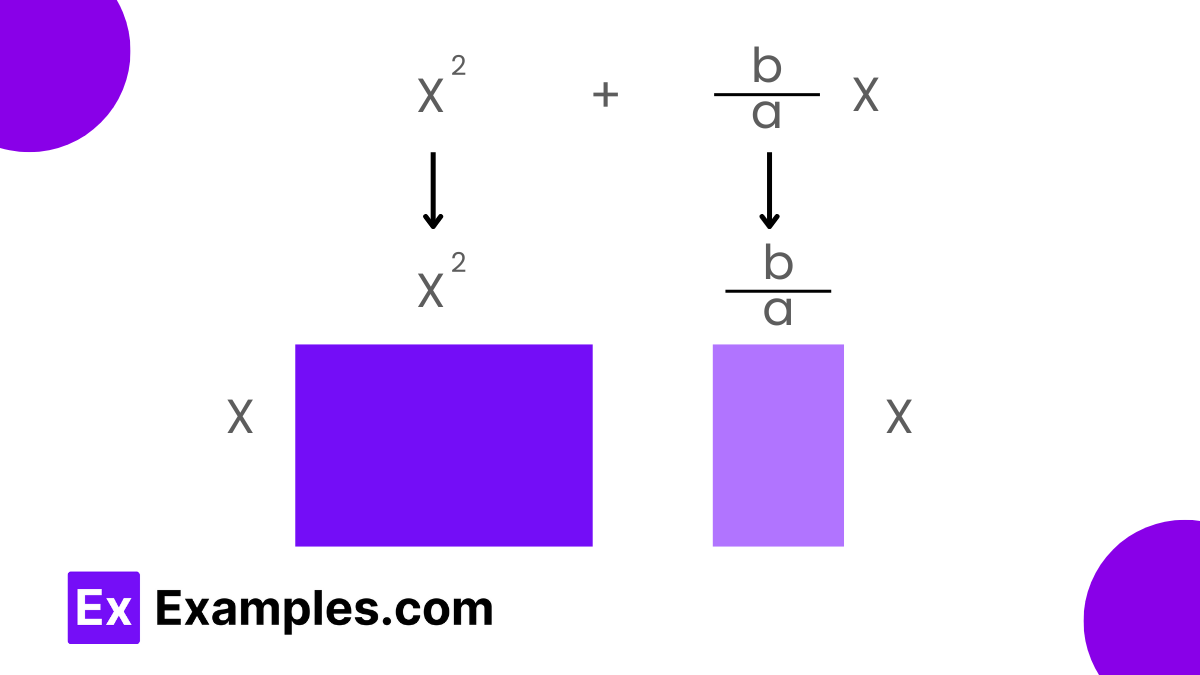
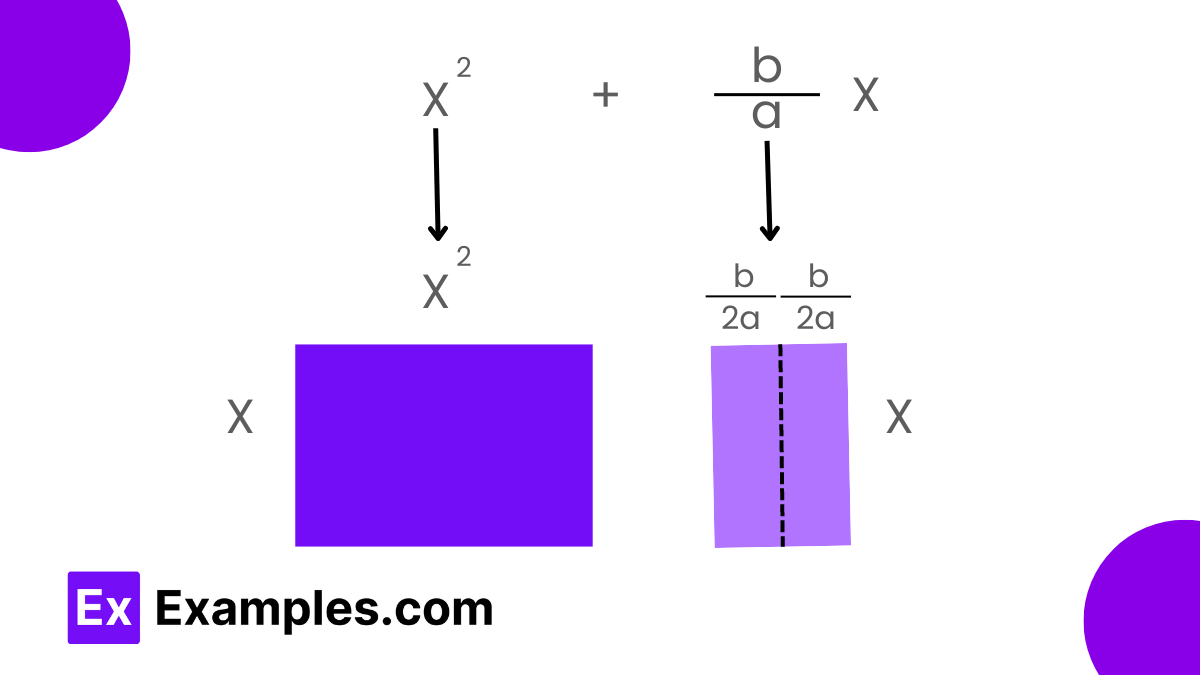
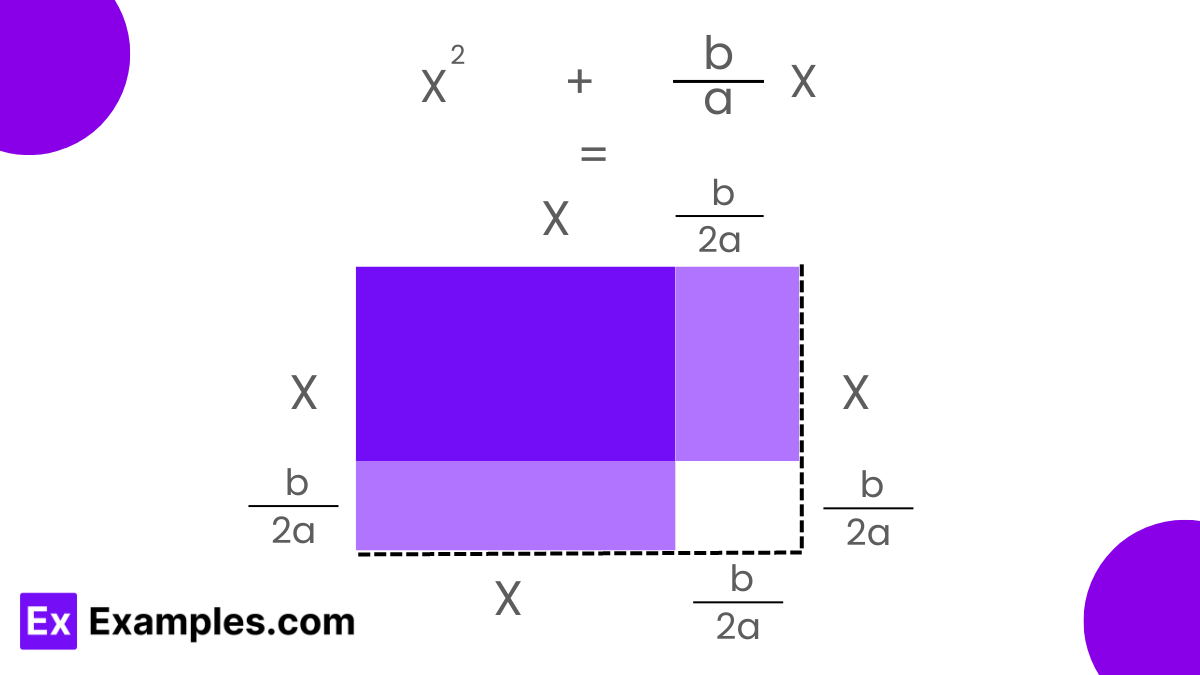
To complete the square for a quadratic expression like 𝑎𝑥²+𝑏𝑥+𝑐, the first step is to factor out 𝑎a to normalize the coefficient of 𝑥² to 1. This transforms the equation into 𝑎[𝑥²+𝑏𝑎𝑥+𝑐𝑎]. Focusing on the first two terms, 𝑥² and (𝑏/𝑎)𝑥, we then calculate half the coefficient of 𝑥, which is 𝑏/2𝑎​. Squaring this value yields 𝑏²/4𝑎²​. We add and subtract this square inside the expression, creating a perfect square trinomial. The equation now looks like 𝑥²+(𝑏/𝑎)𝑥 = (𝑥+𝑏/2𝑎)²−𝑏²4𝑎²​. By substituting this back into the original equation, we obtain 𝑎𝑥²+𝑏𝑥+𝑐 = 𝑎[(𝑥+𝑏/2𝑎)²−𝑏²4𝑎²]+𝑐. Expanding this and simplifying gives the quadratic equation in completed square form: 𝑎(𝑥+𝑏/2𝑎)²+(𝑐−𝑏²/4𝑎). This transformation provides an easy way to see the vertex of the parabola described by the quadratic equation and simplifies further calculations.

Trick to Learn Completing the Square Method

• Normalize the Quadratic Coefficient:
  If the coefficient of 𝑥² isn’t 1, factor it out of the first two terms to ensure the quadratic coefficient is 1.
• Add and Subtract the Missing Square:
  Take half the coefficient of 𝑥, square it, and add and subtract this value after the 𝑥 term. This completes the square inside the expression.
• Simplify into Completed Square Form:
  Rewrite the expression in the form (𝑥+𝑚)² by factoring the trinomial and adjust the constants outside to find the final expression in the form 𝑎(𝑥+𝑚)²+𝑛.

FAQs

What is the purpose of the completing the square method?

The purpose of completing the square is to rewrite a quadratic expression in a different form, specifically 𝑎(𝑥+𝑚)²+𝑛. This transformation makes it easier to solve quadratic equations and identify the vertex of a parabola.

How do you handle a quadratic equation if the coefficient of 𝑥²is not 1?

If the coefficient of 𝑥² isn’t 1, factor out that coefficient from the quadratic and linear terms to normalize it to 1. For example, with 4𝑥²+8𝑥, factor out 4 to get 4(𝑥²+2𝑥).

What does adding and subtracting the square achieve in the completing the square method?

Adding and subtracting the square helps create a perfect square trinomial. This trinomial can then be rewritten as a squared binomial, which is essential to putting the quadratic equation into the desired completed square form.

How does completing the square relate to the quadratic formula?

Completing the square is a method that can be used to derive the quadratic formula. It transforms the quadratic equation into a form where taking the square root directly reveals the values of 𝑥.

Is completing the square useful for equations beyond simple quadratics?