Divisors

The comprehensive guide on divisors, your essential resource for mastering mathematical concepts with ease. This section unravels the mystery of divisors through detailed examples and clear explanations, ensuring a deep understanding of how numbers relate and interact. From the basics of division to exploring prime and composite numbers, our guide enriches your mathematical knowledge, making complex ideas accessible. Whether you’re a student, educator, or math enthusiast, discover the fascinating world of divisors and enhance your numerical skills today.

What is a Divisor?

A divisor is a number that can be divided into another number without leaving a remainder. In simple English, if you have two numbers and you can divide the first number by the second one completely (meaning it divides evenly), then the second number is called a divisor of the first number. For example, if you divide 10 by 2, the result is 5 with no remainder left over, making 2 a divisor of 10.

How to Find Divisor?

Finding divisors of a number involves identifying all the numbers that divide into it without leaving a remainder. Let’s go through the process with an example to make it clearer.

We can represent the divisor in three different ways;

 

 Find the Divisors of 36?

1. Start with 1 and the Number Itself: The first two divisors of any number are always 1 and the number itself because 1 divides into everything and every number is divisible by itself. So, for 36, we have 1 and 36.
2. Check for Divisibility:
   • Begin with the smallest prime number, 2. Does 36 divide evenly by 2? Yes, because 36 is an even number. So, 2 is a divisor.
   • Divide 36 by 2 to find its corresponding divisor: 36÷2=18. So, 18 is also a divisor.
3. Continue with the Next Numbers:
   • Next, check 3. Is 36 divisible by 3? Yes, 36÷3=12 so 3 and 12 are divisors.
   • Check 4: 36÷4=9, so 4 and 9 are divisors.
   • Check 5: 36 is not divisible by 5 (since it doesn’t end in 0 or 5), so we skip it.
   • Check 6: 36÷6=6, so 6 is a divisor. Notice we’ve reached a point where our divisor (6) matches the quotient, meaning we’ve found all possible divisors of 36.
4. List All Divisors: After checking divisibility and listing down the divisors, we conclude that the divisors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36

Divisor Formula

Formula to find the Divisor: Dividend ÷ Divisor = Quotient​

Given:

• Dividend = 30
• Quotient = 5

Divisor=30 ÷6=5

Explanation of Terms:

• Dividend (30): The number you want to divide.
• Quotient (5): The result of the division (how many times the divisor fits into the dividend).
• Divisor (6): The number by which the dividend is divided to get the quotient

Let’s go through a few examples to understand what the dividend, divisor, and remainder are in each case.

lets’s take Division: 15 ÷ 4

Dividend: 15 (The number we are dividing)

Divisor: 4 (The number by which we divide)

Operation: When we divide 15 by 4, we get 3 as a quotient with a remainder.

Quotient: 3 (The whole number result of the division)

Remainder: 3 (Because 15−(4×3)=3)

lets’s take Division:  20 ÷ 3

Dividend: 20 (The number we are dividing)

Divisor: 3 (The number by which we divide)

Operation: Dividing 20 by 3 gives us a quotient with a remainder.

Quotient: 6 (The whole number result of the division)

Remainder: 2 (Because 20−(3×6)=2)

Difference Between Factors and Divisors

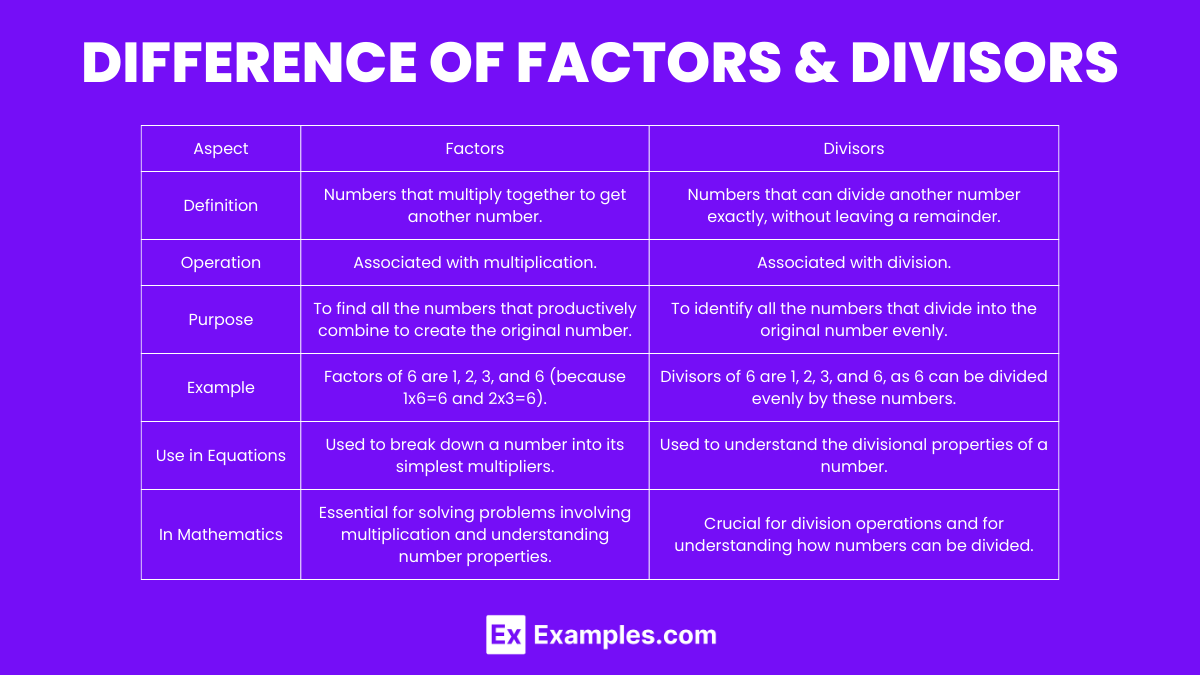When exploring the realm of mathematics, particularly division and multiplication, the terms “factors” and “divisors” often come up. Although they are closely related and sometimes used interchangeably, there are subtle differences worth noting. This comprehensive guide aims to clarify these differences in a structured manner, enhancing your understanding of these fundamental concepts.

Before diving into the differences, let’s establish a foundational understanding of each term:

• Factors are numbers that can be multiplied together to produce another number. They are integral to multiplication operations.
• Divisors are numbers that can divide another number without leaving a remainder, primarily associated with division operations.

Aspect	Factors	Divisors
Definition	Numbers that multiply together to get another number.	Numbers that can divide another number exactly, without leaving a remainder.
Operation	Associated with multiplication.	Associated with division.
Purpose	To find all the numbers that productively combine to create the original number.	To identify all the numbers that divide into the original number evenly.
Example	Factors of 6 are 1, 2, 3, and 6 (because 1×6=6 and 2×3=6).	Divisors of 6 are 1, 2, 3, and 6, as 6 can be divided evenly by these numbers.
Use in Equations	Used to break down a number into its simplest multipliers.	Used to understand the divisional properties of a number.
In Mathematics	Essential for solving problems involving multiplication and understanding number properties.	Crucial for division operations and for understanding how numbers can be divided.
Interchangeability	While all factors of a number can be considered its divisors, the term is more specific to the multiplication context.	While all divisors can be considered factors, the term is more tailored to the division context.

Properties of Divisors

Diving into the realm of mathematics, the concept of divisors plays a pivotal role in understanding the structure and relationships between numbers. Divisors, by definition, are integers that can divide another integer exactly, leaving no remainder. This guide explores the essential properties of divisors, shedding light on their significance and application in various mathematical contexts. Let’s unravel the properties that make divisors a fundamental element in the study of numbers.

Integral Nature of Divisors

All divisors are integers. This means that for any two integers $a$ and $b$, if  $b$ is a divisor of $a$, then the result of $a÷b$ is also an integer. This property underscores the discrete nature of divisors, distinguishing them from fractions or decimals.

Divisors of One and Itself

Every non-zero integer is a divisor of itself, and every integer has at least two divisors: one and itself. This universal property highlights the inclusivity of divisors across the number spectrum, from negative integers to positive integers.

Positive and Negative Divisors

For every positive divisor of a number, there exists a corresponding negative divisor. If $d$ is a divisor of $n$, then $-d$ is also a divisor of $n$. This duality extends the concept of divisors beyond positive integers, embracing the complete integer set.

Divisors and Multiples Relationship

The relationship between divisors and multiples is reciprocal. If $a$ is a divisor of $b$, then $b$ is a multiple of  $a$. This interconnection provides a framework for understanding how numbers interrelate through division and multiplication.

Prime and Composite Divisors

Divisors can be categorized into prime divisors, which are prime numbers, and composite divisors, which are composite numbers. This classification is crucial for factorization processes, where numbers are broken down into their prime divisors to simplify mathematical expressions or solve problems.

Divisibility Rules

Certain divisibility rules help identify divisors of numbers, such as divisibility by 2 for even numbers, by 3 if the sum of digits is divisible by 3, and so on. These rules offer shortcuts to finding divisors without exhaustive division.

Unique Factorization

The Fundamental Theorem of Arithmetic states that every integer greater than 1 either is prime itself or can be factored into prime numbers, which are its prime divisors. This property ensures that the prime factorization of a number is unique, barring the order of factors.

Find Divisors of 12

To find all the divisors of 12, we look for numbers that can divide 12 without leaving a remainder.

1. 1 is a divisor (1 × 12 = 12).
2. 2 is a divisor (2 × 6 = 12).
3. 3 is a divisor (3 × 4 = 12).
4. 4 is a divisor (4 × 3 = 12).
5. 6 is a divisor (6 × 2 = 12).
6. 12 is a divisor of itself (12 × 1 = 12).

Divisors of 12: 1, 2, 3, 4, 6, 12.

Find Divisors of 18

Now, let’s find all the divisors of 18.

1. 1 is a divisor (1 × 18 = 18).
2. 2 is  a divisor since 18 is evenly divisible by 2.
3. 3 is a divisor (3 × 6 = 18).
4. 6 is a divisor (6 × 3 = 18).
5. 9 is a divisor (9 × 2 = 18).
6. 18 is a divisor of itself (18 × 1 = 18).

Divisors of 18: 1, 2, 3, 6, 9, 18.

Find Divisors of 28

Let’s find all the divisors of 28.

1. 1 is a divisor (1 × 28 = 28).
2. 2 is a divisor (2 × 14 = 28).
3. 4 is a divisor (4 × 7 = 28).
4. 7 is a divisor (7 × 4 = 28).
5. 14 is a divisor (14 × 2 = 28).
6. 28 is a divisor of itself (28 × 1 = 28).

Divisors of 28: 1, 2, 4, 7, 14, 28.

Find Divisors of 15

Finally, let’s find all the divisors of 15.

1. 1 is a divisor (1 × 15 = 15).
2. 3 is a divisor (3 × 5 = 15).
3. 5 is a divisor (5 × 3 = 15).
4. 15 is a divisor of itself (15 × 1 = 15).

Divisors of 15: 1, 3, 5, 15.

Positive Divisors

Positive divisors are integral parts of understanding a number’s composition. These divisors are key in various mathematical applications such as factoring numbers, determining prime numbers, and calculating the greatest common divisors (GCD) between numbers.

• Factoring: When breaking down a number into its factors, you’re essentially listing out all positive divisors of that number. For instance, factoring 12 would involve identifying 1, 2, 3, 4, 6, and 12 as its positive divisors.
• Prime Numbers: A prime number is a special case where its only positive divisors are 1 and itself, highlighting the significance of divisors in classifying numbers.

Negative Divisors

Negative divisors extend the concept of divisibility into the realm of negative numbers, offering a complete understanding of a number’s divisibility. They mirror the properties of positive divisors but are negative in value.

• Symmetry in Divisibility: The presence of negative divisors indicates the symmetry in the number line where for every positive divisor, there’s an equivalent negative divisor. This is crucial in solving equations and understanding number theory, where negative values play roles.
• Application in Equations: Negative divisors are particularly useful in algebra, where solving equations might require considering both positive and negative solutions to fully understand the scope of possible answers

In conclusion, understanding divisors is fundamental to mastering key mathematical concepts. By exploring the divisors of numbers, we uncover the intricate relationships and patterns within mathematics. This knowledge not only enhances our problem-solving skills but also deepens our appreciation for the discipline’s beauty and complexity. Embracing the study of divisors opens doors to a richer, more connected understanding of the mathematical world.