Exponents

What are Exponents?

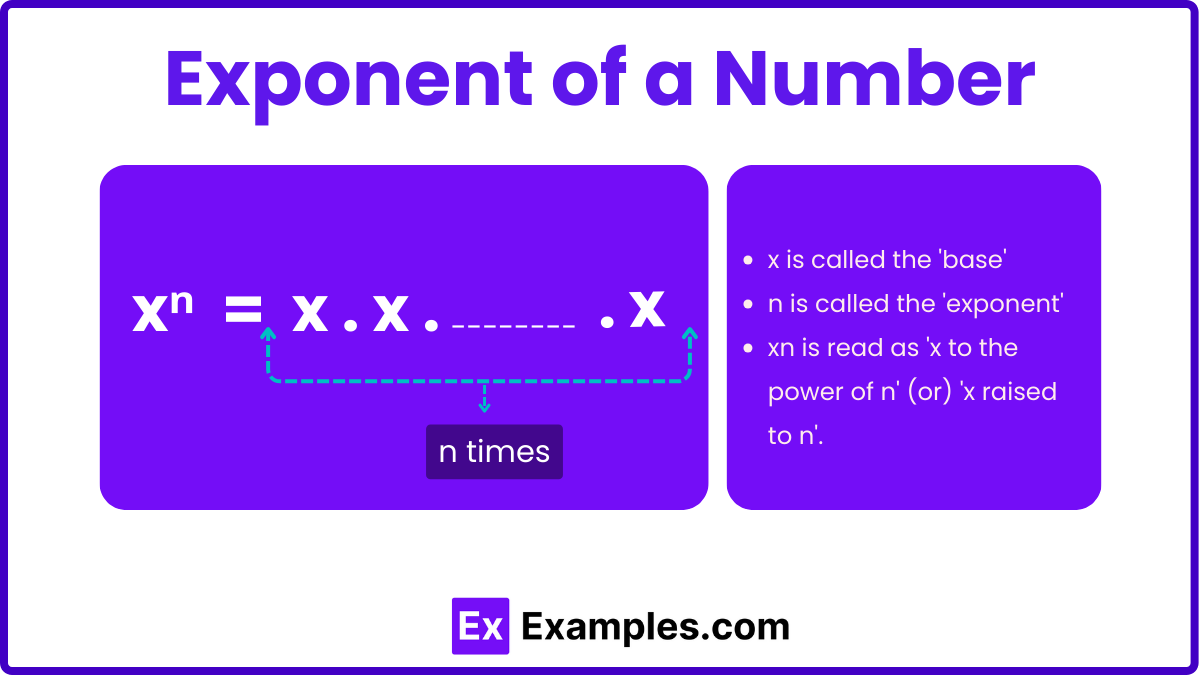
Exponents are a fundamental concept in mathematics used to express repeated multiplication of the same number. An exponent tells us how many times to multiply a base number by itself. This operation is often called “raising to a power.”

Exponent Table

Formulas

Types of Exponents

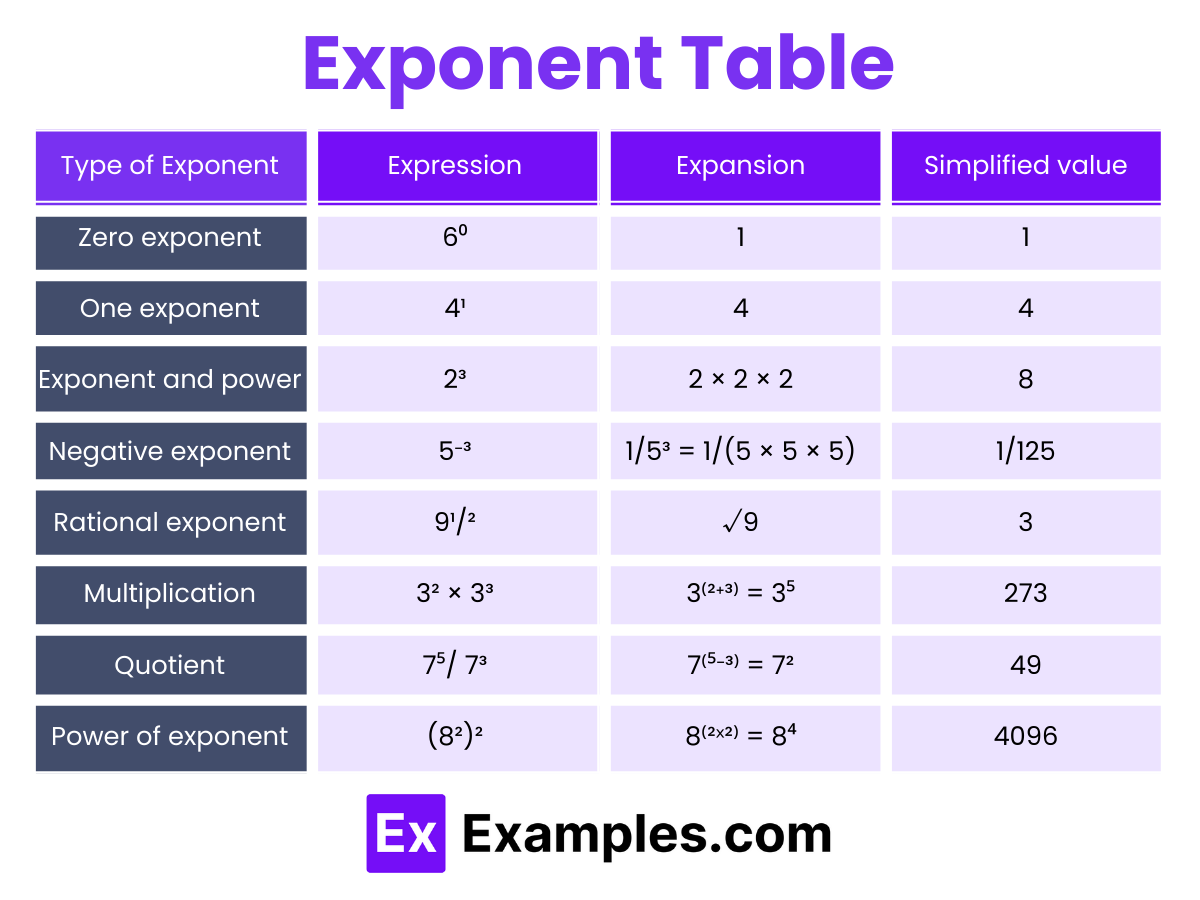
Exponents are mathematical expressions that simplify the process of multiplying a number by itself multiple times. Understanding different types of exponents is crucial for handling complex calculations effectively. Here’s a look at the various types of exponents and their specific characteristics:

1. Positive Exponents

• Description: A positive exponent tells how many times to multiply the base number by itself.
• Example: 5³ means 5×5×5=125

2. Zero Exponents

• Description: Any non-zero base raised to the power of zero equals one.
• Example: 7⁰=1

3. Negative Exponents

• Description: A negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent.
• Example: 2⁻³means 1/2³=1/8

4. Fractional Exponents

• Description: A fractional exponent, where the numerator is a power and the denominator is a root, simplifies to taking the root of the base raised to the power of the numerator.
• Example: 16¹/² represents the square root of 16, which is 4.

5. Rational Exponents

• Description: Similar to fractional exponents, rational exponents represent powers and roots but with potentially more complex fractions.
• Example: 8²/³ means the cube root of 8 squared, which is 4.

6. Irrational Exponents

• Description: These exponents are represented by irrational numbers and often arise in advanced mathematics and physics.
• Example: 𝑒𝜋, where 𝑒 is Euler’s number and 𝜋 is pi.

7. Complex Exponents

• Description: Complex exponents involve a complex number in the exponent and are used in higher-level mathematics, particularly in the study of waves and oscillations.
• Example: 𝑒ᶦπ equals −1, according to Euler’s formula.

Properties of Exponents

Exponents are a key element in algebra that facilitate the manipulation and simplification of expressions involving powers of numbers or variables. Understanding the properties of exponents is essential for efficient problem-solving. Here’s a comprehensive guide to the main properties:

1. Product of Powers Property

• Rule: When multiplying powers with the same base, add their exponents.
• Formula: 𝑎ᵐ×𝑎ⁿ=𝑎ᵐ⁺ⁿ
• Example: 𝑥²×𝑥³=𝑥²⁺³=𝑥⁵

2. Quotient of Powers Property

• Rule: When dividing powers with the same base, subtract the exponent of the denominator from the exponent of the numerator.
• Formula: 𝑎ᵐ/𝑎ⁿ=𝑎ᵐ⁻ⁿ
• Example: 𝑥⁵/𝑥²=𝑥⁵⁻³=𝑥³

3. Power of a Power Property

• Rule: When raising a power to another power, multiply the exponents.
• Formula: (𝑎ᵐ)ⁿ=𝑎ᵐˣⁿ
• Example: (𝑥²)³=𝑥²ˣ³=𝑥⁶

4. Power of a Product Property

• Rule: When raising a product to a power, raise each factor of the product to the power.
• Formula: (𝑎𝑏)ⁿ=𝑎ⁿ×𝑏ⁿ
• Example: (2𝑥)³=2³ . x³ =8𝑥³

5. Power of a Quotient Property

• Rule: When raising a quotient to a power, raise both the numerator and the denominator to the power.
• Formula: (𝑎/𝑏)ⁿ=𝑎ⁿ/𝑏ⁿ​
• Example: (𝑥𝑦)²=𝑥²/𝑦²

6. Zero Exponent Property

• Rule: Any non-zero base raised to the power of zero equals one.
• Formula: 𝑎⁰=1 (where 𝑎≠0)
• Example: 5⁰=1

7. Negative Exponent Property

• Rule: A negative exponent represents the reciprocal of the base raised to the absolute value of the exponent.
• Formula: 𝑎⁻ⁿ=1/𝑎ⁿ (where 𝑎≠0)
• Example:
• 2⁻³=1/2³=1/8

Tips and Tricks for Exponent:

Handling exponents effectively is key to solving algebraic expressions and equations efficiently.

• If a fraction has a negative exponent, then we take the reciprocal of the fraction to make the exponent positive, i.e., (a/b)^-m = (b/a)^m.
• Decimal exponents can be solved by first converting the decimal into fraction form, i.e., 2^0.5 can be written as 2^1/2

How to find Exponents

Problem 1: Basic Exponents

Problem: Calculate 2³

Solution: 2³=2×2×2=8

Answer: 8

Problem 2: Negative Exponents

Problem: Evaluate 5⁻².

Solution: 5⁻²=1/5²=1/25

Answer: 1/25

Problem 3: Fractional Exponents

Problem: Simplify 16¹/².

Solution: 16¹/²=16=4.

Answer: 4

Problem 4: Product of Powers

Problem: Simplify (3²)×(3³).

Solution: (3²)×(3³)=3²⁺³=3⁵=243

Answer: 243

Problem 5: Quotient of Powers

Problem: Simplify 2⁸/2³ Solution: 2⁸/2³=2⁸⁻³=2⁵ Answer: 32

Problem 6: Power of a Power

Problem: Calculate (4²)³.

Solution: (4²)³=4²×3=46=4096

Answer: 4096

Problem 7: Zero Exponent

Problem: What is 7⁰?

Solution: Any non-zero number raised to the power of zero equals 1.

Answer: 1

FAQs

What are the 7 Rules of Exponents?

The seven rules of exponents are: product of powers, quotient of powers, power of a power, power of a product, power of a quotient, zero exponent, and negative exponent. These rules simplify expressions and solve equations involving powers.

How to Calculate Exponent?

To calculate an exponent, multiply the base (the number) by itself as many times as indicated by the exponent. For example, 3⁴ means multiplying 3 by itself four times: 3×3×3×3=81

How to Explain Exponents to a Child?

Exponents can be explained to children as a shortcut for multiplication. Tell them it shows how many times to use the number in a multiplication. For example, 5 means multiplying 5 by itself three times: 5×5×5

What are Exponents for Dummies?

Exponents are a way to express repeated multiplication. Instead of writing a number many times, you can use an exponent to tell how many times to multiply a number by itself. They simplify numbers and calculations, especially with large values.

What is 2 Raised to Power 16?

Two raised to the power of 16 is 216, which equals 65,536. It is the result of multiplying 2 by itself 16 times.

What is 2 Raised to Power 9?

Two raised to the power of 9 is 29, which equals 512. This results from multiplying 2 by itself nine times.