Functions

What are Functions?

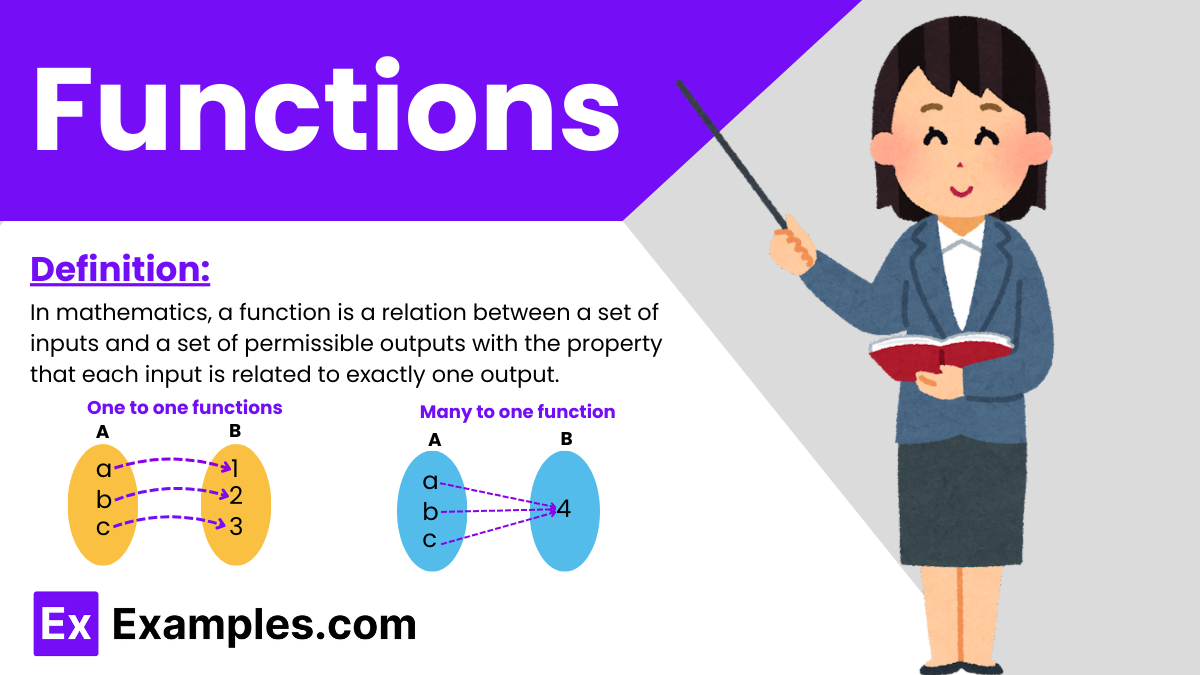
In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Functions are fundamental to many areas of mathematical, scientific, and engineering disciplines, encapsulating the idea of a deterministic relationship where one quantity completely determines another.

Types of Functions in Maths

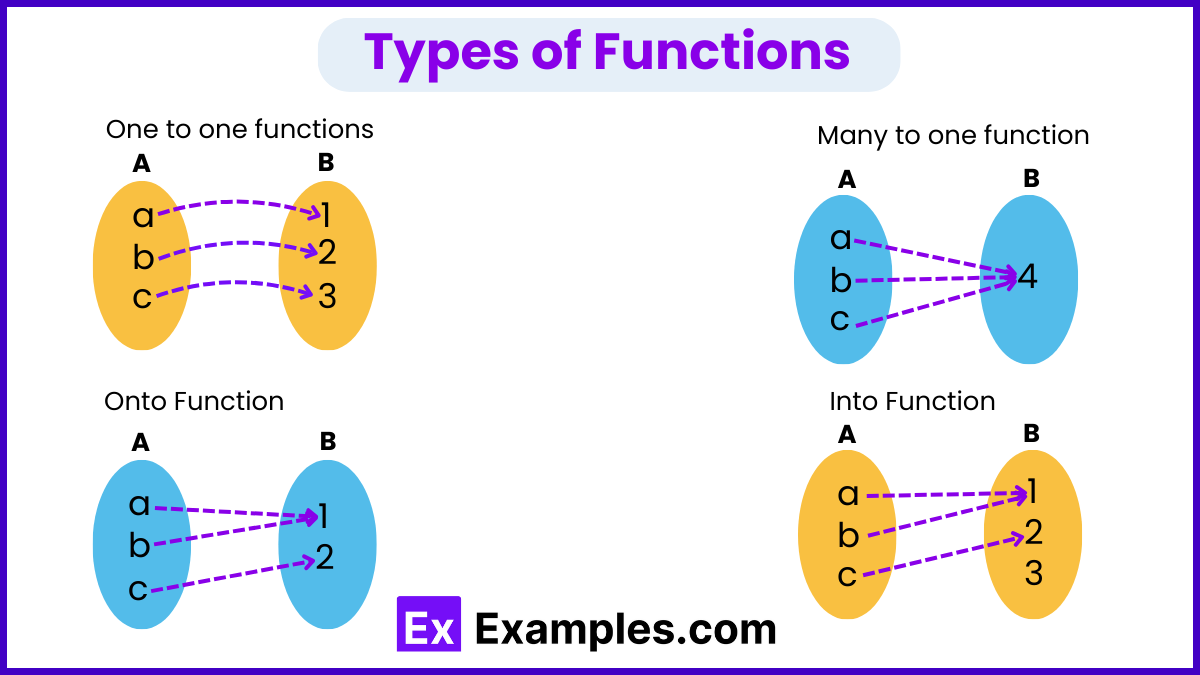
In mathematics, functions can be classified based on how they map elements from the domain (set of all possible input values) to the codomain (set of all potential output values). Understanding these different types of functions is crucial for analyzing mathematical relationships and solving problems across various fields. Here’s an overview of some fundamental types of functions:

1. One-To-One Function (Injective Function)

• Definition: A function 𝑓:𝐴→𝐵 is one-to-one (injective) if it maps each element of the domain 𝐴 to a unique element in the codomain 𝐵. That is, no two different elements in the domain correspond to the same element in the codomain.
• Mathematical Expression: 𝑓(𝑥₁)=𝑓(𝑥₂) implies 𝑥₁=𝑥₂

2. Onto Function (Surjective Function)

• Definition: A function f:A→B is onto if every element in the codomain B is the image of at least one element in the domain A. Essentially, the function covers the entire codomain.
• Example: The function 𝑓(𝑥)=𝑥²−4 defined from the real numbers to the set of all real numbers less than or equal to -4 or greater than or equal to 0 is onto.

3. Polynomial Functions

• Definition: A polynomial function is a function that involves only non-negative integer powers of x. It is expressed in the form 𝑓(𝑥)=𝑎ₙ𝑥ⁿ⁻¹+𝑎ₙ₋₁𝑥ⁿ⁻¹+…+𝑎₁𝑥+𝑎₀, where 𝑎ₙ,𝑎ₙ₋₁,…,𝑎₀ are constants.
• Example: 𝑓(𝑥)=4𝑥³−3𝑥²+2𝑥−1 is a polynomial function.

4. Inverse Functions

• Definition: If a function 𝑓 has an inverse, then the inverse function, denoted as 𝑓−1, reverses the mapping of 𝑓. For the function 𝑓 and its inverse 𝑓−1\, the relation 𝑓(𝑓−1(𝑦))=𝑦 and 𝑓−1(𝑓(𝑥))=𝑥 hold true for all 𝑥 in the domain of 𝑓 and 𝑦 in the domain of 𝑓−1.
• Example: If 𝑓(𝑥)=3𝑥+4, then its inverse 𝑓−1(𝑥)=𝑥−43

5. Even Function

• Definition: A function 𝑓 is called an even function if for every 𝑥 in the domain of 𝑓, the equality 𝑓(−𝑥)=𝑓(𝑥)holds true. The graph of an even function is symmetric with respect to the y-axis.
• Example: 𝑓(𝑥)=𝑥² is an even function because 𝑓(−𝑥)=(−𝑥)²=𝑥²=𝑓(𝑥)

Function in Algebra

A function in algebra is often written as 𝑓(𝑥), where 𝑓 denotes the function and x represents the input variable. The output of the function, 𝑓(𝑥), depends on the input value 𝑥.

f(x) = aⁿxⁿ + a^{n – 1}x^{n – 1}+ a^n-2x^n-2+ ……. ax + c.

For example:

• y = 4x + 3
• y = 8x – 4
• y = 9y
• y = 6/x

List of Types of Functions

Type	Functions
Based on Mapping
One One Function	Maps each element of the domain to a unique element in the codomain.
Many One Function	Maps multiple elements of the domain to a single element in the codomain.
Onto Function	Covers every element of the codomain.
One One and Onto Function	Bijective function, both one-to-one and onto.
Into Function	Does not map to every element of the codomain.
Based on Degree
Constant Function	Outputs the same value for any input.
Identity Function	Outputs the input itself.
Linear Function	First-degree polynomial with no exponents or powers greater than one.
Quadratic Function	Second-degree polynomial.
Cubic Function	Third-degree polynomial.
Polynomial Functions	Functions that can be represented by polynomials.
Based on Math Concepts
Algebraic Functions	Functions involving polynomial expressions.
Trigonometric Functions	Functions involving angles and ratios of triangle sides.
Inverse Trigonometric Functions	Functions that reverse trigonometric functions.
Logarithmic and Exponential Functions	Functions involving logarithms and exponents.
Miscellaneous Functions
Modulus Function	Outputs the absolute value of the input.
Rational Function	Ratio of two polynomial functions.
Signum Function	Indicates the sign of a number.
Even and Odd Functions	Symmetric functions relative to the y-axis or origin.
Periodic Functions	Functions that repeat their values at regular intervals.
Greatest Integer Function	Rounds down to the nearest integer.
Inverse Function	Reverses another function.

What is a function on a graph?

A function 𝑓(𝑥) can be visualized on a graph by plotting points that represent the relationship between each input value 𝑥 and its corresponding output 𝑦=𝑓(𝑥). To create this graph, you select various values for 𝑥, compute the corresponding 𝑦 values, and then plot these (x, y) pairs on a coordinate plane. Here’s an illustrative example:

Suppose, y = x + 3

Then,

• when x = 0, y = 3
• when x = -2, y = -2 + 3 = 1
• when x = -1, y = -1 + 3 = 2
• when x = 1, y = 1 + 3 = 4
• when x = 2, y = 2 + 3 = 5

Trigonometric Functions

The six fundamental trigonometric functions are defined as follows: 𝑓(𝜃)=sin⁡𝜃, 𝑓(𝜃)=cos⁡𝜃, 𝑓(𝜃)=tan⁡𝜃, 𝑓(𝜃)=sec⁡𝜃, 𝑓(𝜃)=csc⁡𝜃, and 𝑓(𝜃)=cot⁡𝜃. Here, the domain variable 𝜃 represents an angle, which can be measured in either degrees or radians. These trigonometric functions are derived from the ratios of the sides of a right triangle and are fundamentally linked to the principles of the Pythagorean theorem

Tips for using function

1. Understand the Basics: Grasp the key concepts like domain, range, and function notation to lay a strong foundation.
2. Visualize with Graphs: Plotting functions on a graph can help visualize relationships and behaviors such as intercepts and asymptotes.
3. Practice with Examples: Work through various examples to become familiar with different types of functions, including linear, quadratic, and exponential.
4. Use Technology: Leverage graphing calculators or software for complex functions and to check your work.
5. Connect Concepts: Relate functions to real-world scenarios to better understand their practical applications.
6. Master Inverses and Composites: Learn how to find and use inverse and composite functions, as these are crucial in higher mathematics

FAQs

What’s Your Function Mean?

A function defines a specific relationship where each input has a single output. It’s a way to express one quantity as dependent on another.

How Do You Describe Functions?

Functions are described by their rules, domain (inputs), and range (outputs). They map each element of the domain to one element in the range.

What Does It Mean When Something Is a Function of Something?

When something is a function of something else, it means that the first variable’s value depends on the second. Changes in the second variable directly affect the first.

What is One Example of a Function in Real Life?

A real-life example of a function is the relationship between distance traveled and time in a car where speed is constant, described as 𝑑=𝑣𝑡.

What is an Example of One Function?

An example of a simple function is 𝑓(𝑥)=𝑥2, which squares the input value to produce the output.

What is a Function for Dummies?

A function in mathematics is like a machine: you input a number, it performs a set rule (like multiplication or addition), and then outputs a new number based on that rule.