What is the greatest common factor (GCF) of 16 and 40?
4
8
16
24


The greatest common factor (GCF) of 16 and 40 is 8. This can be efficiently determined by several methods such as prime factorization, listing factors, or using the Euclidean algorithm. In prime factorization, 16 is broken down to 2⁴ and 40 to 2³ × 5. Both share the base prime factor 2, with the lowest exponent being 2³, thus the GCF is 2³ = 8. Listing the factors, we find that 16’s factors (1, 2, 4, 8, 16) and 40’s factors (1, 2, 4, 5, 8, 10, 20, 40) also reveal 8 as the largest common factor. The Euclidean algorithm, which involves subtracting the smaller numbers from the larger until the numbers converge, confirms the GCF as 8. This example illustrates a common approach in arithmetic for finding the greatest common divisor, which is essential for simplifying fractions and solving other mathematical problems.
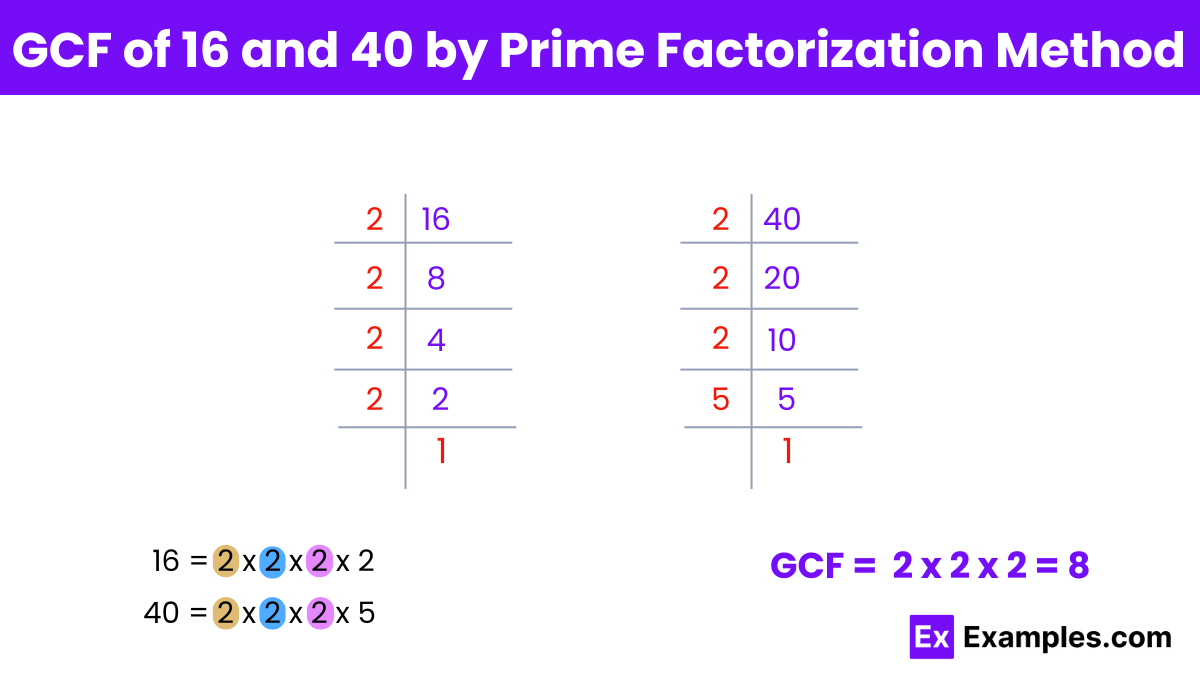
To find the greatest common factor (GCF) of 16 and 40 using the prime factorization method, follow these steps:
Step 1: Prime factorize both numbers:
For 16: 16 = 2⁴
For 40: 40 = 2³ × 5
Step 2: Identify the common prime factors and their lowest powers:
The common prime factor between 16 and 40 is 2. The lowest power of 2 present in both factorizations is 2³.
Step 3: Multiply the common prime factors with their lowest powers to determine the GCF:
GCF = 2³ = 8

To find the greatest common factor (GCF) of 16 and 40 using the long division method, follow these steps:
Step 1: Start by dividing the larger number (40) by the smaller number (16).
40 ÷ 16 = 2 with a remainder of 8.
Step 2: Next, use the remainder as the new divisor and divide the original divisor (16) by it.
16 ÷ 8 = 2 with a remainder of 0.
Since the remainder is now 0, the division process stops here.
Step 3: The divisors at this step where the remainder becomes zero is the greatest common factor (GCF).
GCF = 8.

To find the greatest common factor (GCF) of 16 and 40 by listing common factors:
Step 1: List the factors of each number.
Factors of 16: 1, 2, 4, 8, 16
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Step 2: Identify the common factors.
Step 3: Determine the greatest common factor.
Therefore, the greatest common factor (GCF) of 16 and 40 by listing common factors is 8.
Yes, using division, the remainder sequence finds 8 as the GCF.
List all factors and identify the highest common one between the two lists.
Most scientific calculators have a GCF function, or you can manually calculate using the prime factorization method.
Regular practice with diverse problem sets can ensure proficiency in calculating the GCF.
The method remains the same; prime factorization shows 2⁴ is still the highest common power.
Yes, concepts involving GCF are foundational for advanced studies in number theory and algebra.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the greatest common factor (GCF) of 16 and 40?
4
8
16
24
Which number is a common factor of both 16 and 40?
2
6
10
12
What is the GCF of 16 and 40 using prime factorization?
2
4
8
16
If the GCF of 16 and 40 is used to simplify the fraction 40/16, what is the simplified result?
2/1
5/2
5/4
10/4
Which number is not a factor of both 16 and 40?
2
8
10
16
Which method can be used to find the GCF of 16 and 40?
Subtraction method
Division method
LCM method
Addition method
What is the largest number that divides both 16 and 40 evenly?
4
8
12
16
The GCF of 16 and 40 is equal to which of the following?
The sum of the numbers
The highest common factor
The product of the numbers
The smallest common factor
What is the GCF of 16 and 40 expressed as a product of its prime factors?
2²
2³
2⁴
5 × 8
If you add the GCF of 16 and 40 to 16, what is the result?
20
24
26
28
Before you leave, take our quick quiz to enhance your learning!

