What is the Greatest Common Factor (GCF) of 6 and 15?
1
2
3
5


The Greatest Common Factor (GCF) of 6 and 15 is the largest number that divides both numbers without leaving a remainder. To determine this, we can list the factors of each number: for 6, the factors are 1, 2, 3, and 6, while for 15, the factors are 1, 3, 5, and 15. The common factors between 6 and 15 are 1 and 3. The largest of these common factors is 3. Therefore, the GCF of 6 and 15 is 3, which is useful for simplifying fractions and solving problems involving these numbers.

To find the Greatest Common Factor (GCF) of 6 and 15 using the prime factorization method, follow these steps:
Prime Factorization of Each Number:
Prime factors of 6:
6 = 2 × 3
Prime factors of 15:
15 = 3 × 5
Identify the Common Prime Factors:
The only common prime factor is 3.
Multiply the Common Prime Factors:
GCF = 3
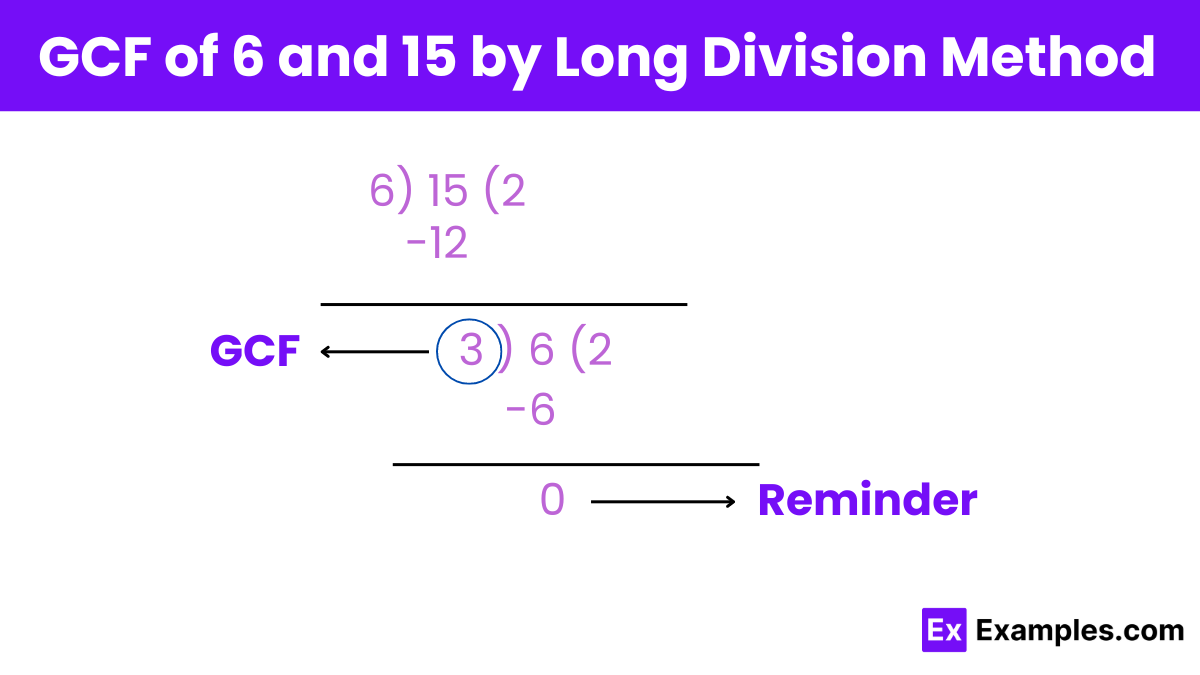
To find the Greatest Common Factor (GCF) of 6 and 15 using the Long Division Method, follow these steps:
Divide the Larger Number by the Smaller Number:
Divide 15 (larger number) by 6 (smaller number).
15 ÷ 6 = 2 remainder 3
Replace the Larger Number with the Smaller Number:
The divisor (6) becomes the new dividend.
The remainder (3) becomes the new divisor.
Repeat the Division:
Now, divide 6 by 3.
6 ÷ 3 = 2 remainder 0
Check the Remainder:
When the remainder is 0, the current divisors is the GCF.
The remainder is 0, and the current divisor is 3.

To find the Greatest Common Factor (GCF) of 6 and 15 by listing their common factors, follow these steps:
List the Factors of Each Number:
Factors of 6: 1, 2, 3, 6
Factors of 15: 1, 3, 5, 15
Identify the Common Factors:
The common factors of 6 and 15 are: 1, 3
Find the Greatest Common Factor:
The largest number in the list of common factors is 3.
There isn’t a single formula, but methods like prime factorization, listing factors, and the Euclidean algorithm are used to find the GCF.
Find the GCF of two numbers first, then use that result to find the GCF with the next number, continuing until all numbers are included.
In number theory, the GCF is fundamental for understanding the relationships between numbers, particularly in modular arithmetic and divisibility.
Yes, the GCF helps in determining the optimal dimensions for dividing materials and resources evenly in construction and other fields.
Understanding the GCF is crucial for simplifying expressions, solving equations, and working with ratios and proportions effectively.
Yes, the Greatest Common Factor (GCF) is also known as the Greatest Common Divisor (GCD).
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the Greatest Common Factor (GCF) of 6 and 15?
1
2
3
5
Which of the following numbers is a common factor of both 6 and 15?
2
3
4
6
How many factors does the GCF of 6 and 15 have?
1
2
3
4
Which number is the largest common factor of 6 and 15?
1
2
3
5
What is the smallest prime factor of the GCF of 6 and 15?
2
3
5
7
Which pair of numbers has the same GCF as 6 and 15?
12 and 18
9 and 21
15 and 30
24 and 36
The GCF of 6 and 15 is also a factor of which of the following numbers?
30
45
60
70
What is the GCF of 6 and 15 multiplied by 5?
15
18
20
25
What is the GCF of 6, 15, and 21?
1
3
6
15
Which of the following numbers is not divisible by the GCF of 6 and 15?
9
15
18
24
Before you leave, take our quick quiz to enhance your learning!

