GCF of 72 and 81
GCF of 72 and 81
The greatest common factor (GCF) of 72 and 81 is 9. To find the GCF, one can use various methods such as prime factorization, listing common factors, or employing the Euclidean algorithm. In this case, both numbers share a common factor of 9, which is the highest integer that divides both 72 and 81 without leaving a remainder. This common factor represents the largest divisor that both numbers have in common, making it the greatest common factor. Therefore, the GCF of 72 and 81 is 9.
GCF of 72 and 81
GCF of 72 and 81 is 9.
GCF of 72 and 81 by Prime Factorization Method.
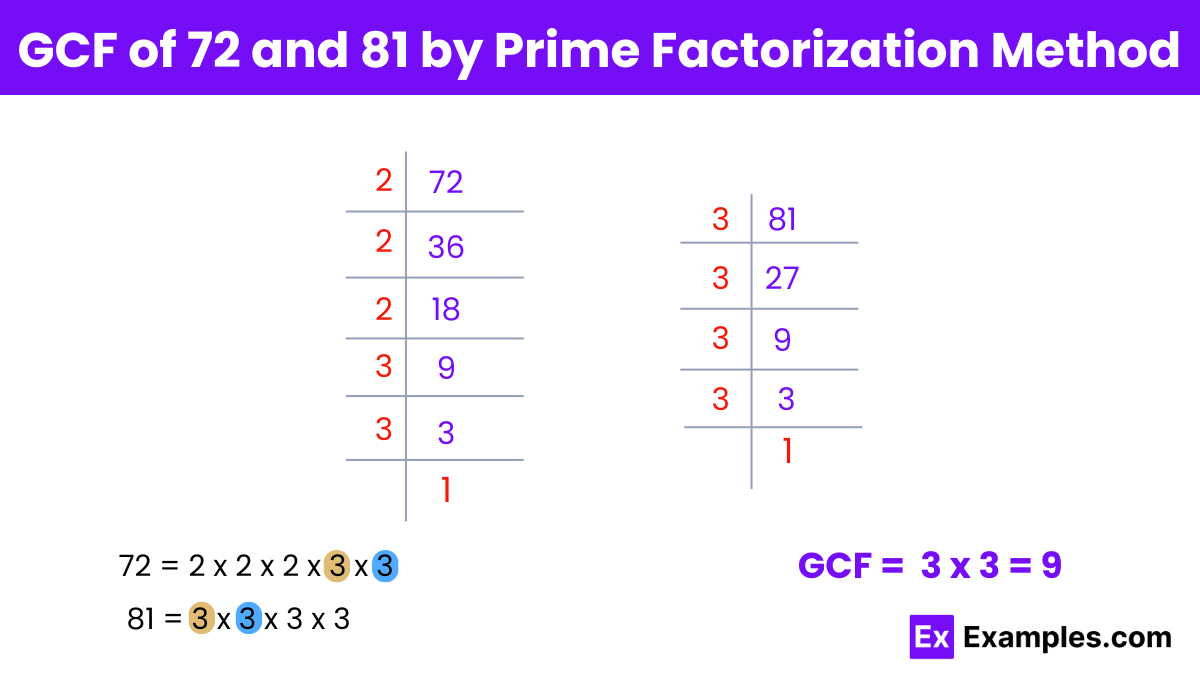
To find the greatest common factor (GCF) of 72 and 81 using prime factorization:
Step 1: Prime factorize both numbers:
For 72 : 72 = 2³ × 3²
For 81 : 81 = 3⁴
Step 2: Identify common prime factors and their lowest powers:
Both 72 and 81 have a common factor of 3, with the lowest power being 2.
Step 3: Multiply the common prime factors: GCF = 3² = 9.
Therefore, the GCF of 72 and 81 is 9.
GCF of 72 and 81 by Long Division Method.
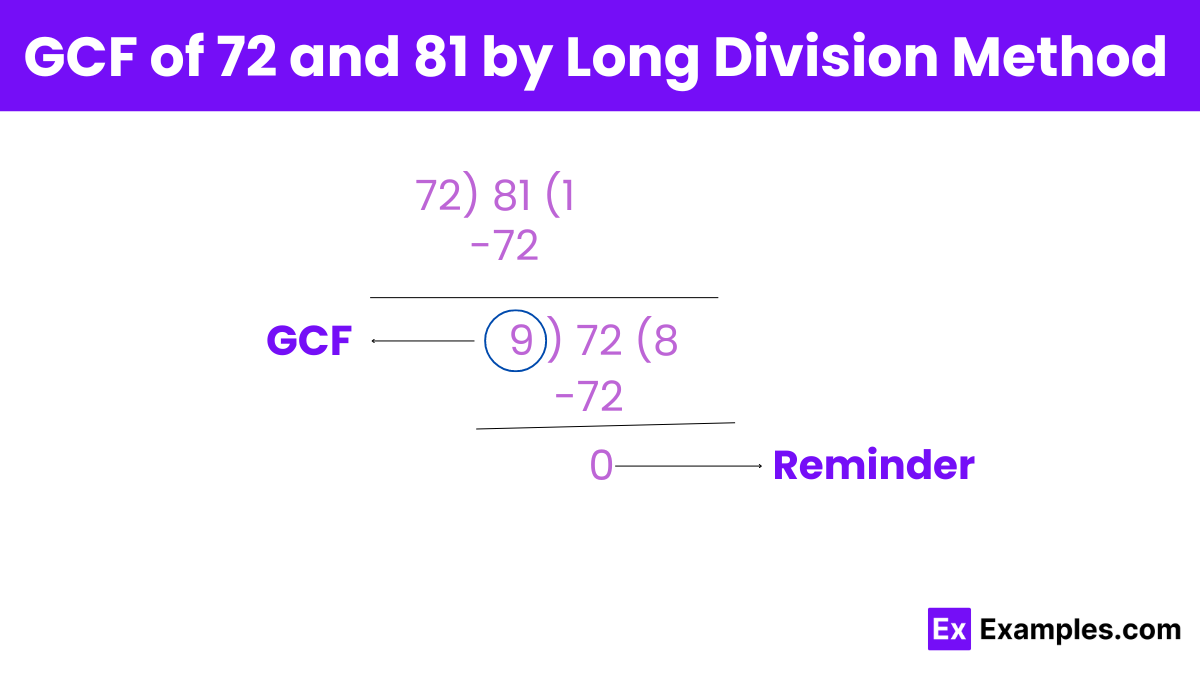
To find the greatest common factor (GCF) of 72 and 81 using the long division method:
Step 1: Start by dividing the larger number (81) by the smaller number (72). 81 ÷ 72 =1 with a remainder of 9.
Step 2: Then, take the divisor (72) and divide it by the remainder (9). 72 ÷ 9 = 8.
Step 3: Continue this process until there is no remainder. 9 ÷ 8 = 1 with a remainder of 1. 8 ÷ 1 = 8. 1÷1=1.
Step 4: The last divisors before reaching 1 is the greatest common factor (GCF). GCF = 1.
GCF of 72 and 81 by Listing Common Factors.
To find the greatest common factor (GCF) of 72 and 81 by listing common factors:
Step 1: List the factors of each number.
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 81: 1, 3, 9, 27, 81
Step 2: Identify the common factors. Common factors: 1, 3, 9
Step 3: Determine the greatest common factor. GCF=9.GCF = 9.GCF=9.
Therefore, the GCF of 72 and 81 by listing common factors is 9.
What is the HCF of the numbers 72 and 81?
The highest common factor (HCF) of 72 and 81 is 9. It represents the largest integer that divides both numbers without leaving a remainder.
What is the LCM of 72 and 81?
The least common multiple (LCM) of 72 and 81 is 648. It is the smallest multiple that is divisible by both 72 and 81.
Can you use the GCF of 72 and 81 to solve problems involving factors and multiples?
Yes, knowing the GCF can help in finding common factors or simplifying problems involving multiples of 72 and 81.
How does the GCF of 72 and 81 relate to the concept of greatest common divisor?
The GCF of 72 and 81 is the greatest common divisor, as it represents the largest divisor common to both numbers.
Can the GCF of 72 and 81 be found using algebraic methods?
Yes, the GCF can be found algebraically by factoring both numbers and identifying common factors.
Are there any other methods to find the GCF of 72 and 81 besides prime factorization?
Yes, methods such as listing common factors or using long division can also be used.
Share :
