What is the area of a triangle with a base of 8 cm and a height of 5 cm?
20 cm²
25 cm²
30 cm²
35 cm²
of 10
Geometry Formulas, 2D & 3D Shapes, Examples
Geometry Formulas, 2D & 3D Shapes, Examples
The formulas used to determine dimensions, perimeter, area, surface area, and volume of both 2D and 3D geometric shapes are known as geometry formulas. 2D shapes include flat figures like squares, circles, and triangles, while 3D shapes encompass forms such as cubes, cuboids, spheres, cylinders, and cones. The basic geometry formulas are as follows:
What are Geometry Formulas?
Geometry formulas are mathematical equations that define relationships between different geometric shapes and figures. These formulas are used to calculate properties such as area, perimeter, volume, and surface area. Understanding geometry formulas is essential for solving various problems in mathematics, physics, engineering, and everyday life.
Basic Geometry Formulas
2D Geometry Formulas
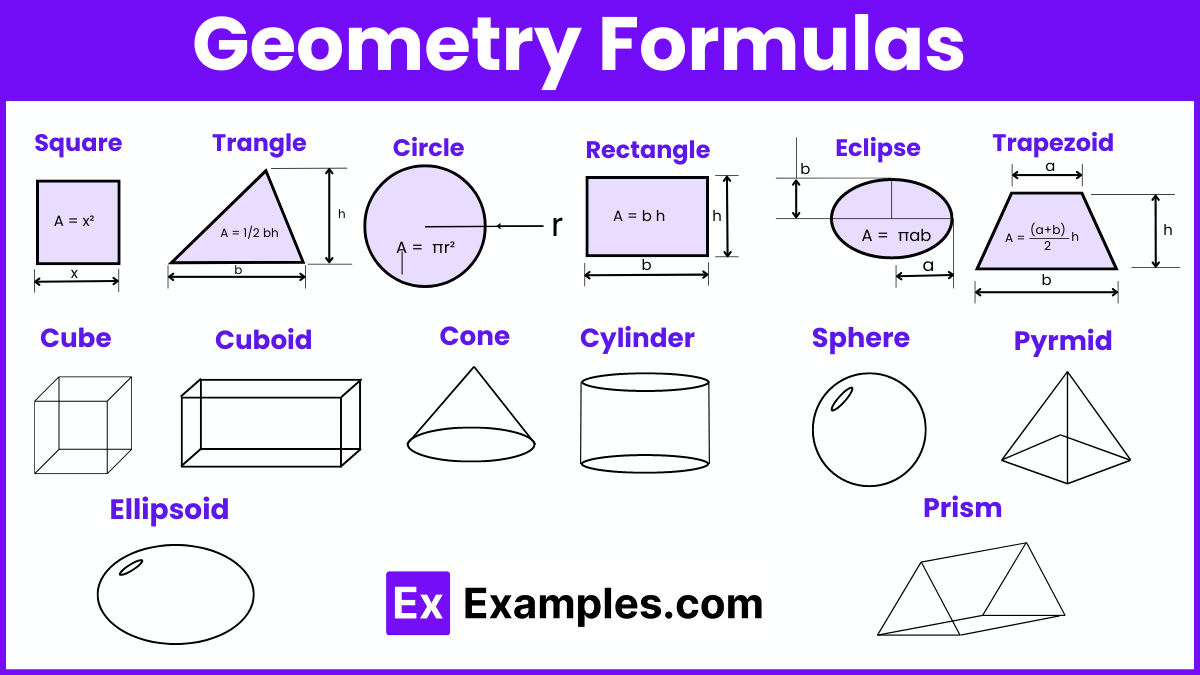
Below is a comprehensive list of various 2D geometry formulas categorized by geometric shape. This includes essential formulas where the mathematical constant π (pi) is used:
Perimeter of a Square = 4(Side)
Perimeter of a Rectangle = 2(Length + Breadth)
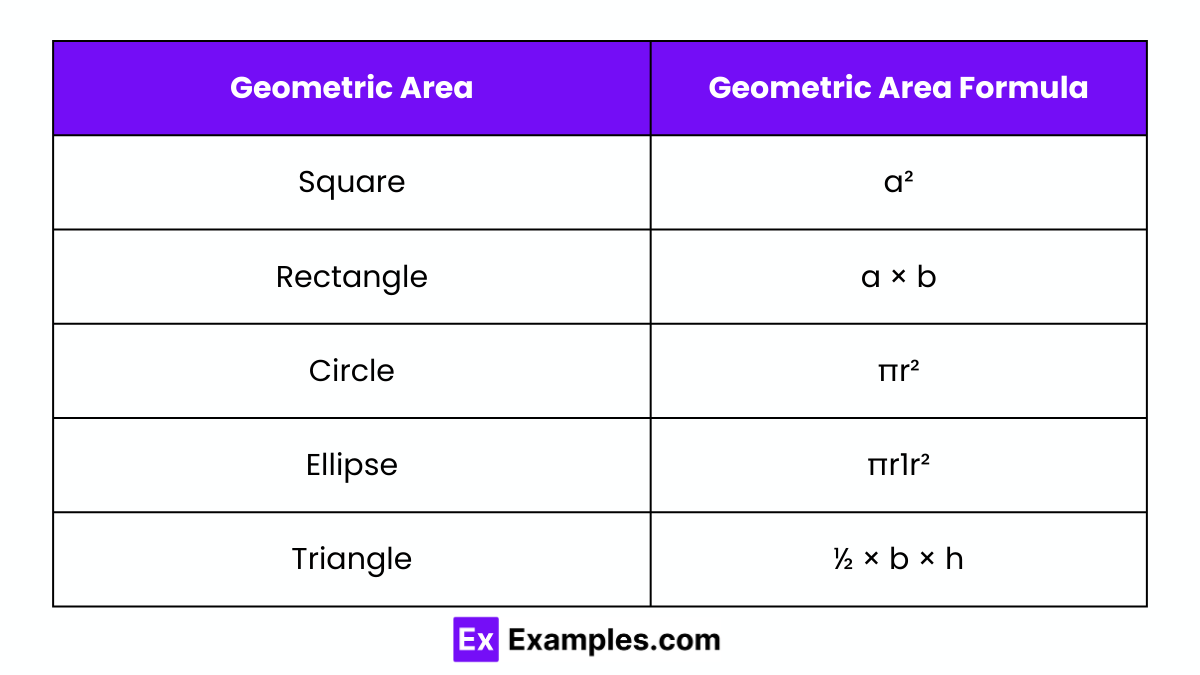
Area of a Square = Side²
Area of a Rectangle = Length × Breadth
Area of a Triangle = ½ × base × height
Area of a Trapezoid = ½ × (base₁ + base₂) × height
Area of a Circle = A = π×r²
Circumference of a Circle = 2πr
3D Geometry Formulas
The basic 3D geometry formulas are as follows. Note that these formulas incorporate the mathematical constant π (pi):
The curved surface area of a Cylinder = 2πrh
Total surface area of a Cylinder = 2πr(r + h)
Volume of a Cylinder = V = πr²h
The curved surface area of a cone = πrl
Total surface area of a cone = πr(r+l) = πr[r+√(h²+r²)]
Volume of a Cone = V = ⅓×πr²h
Surface Area of a Sphere = S = 4πr²
Volume of a Sphere = V = 4/3×πr³
where,
r = Radius;
h = Height. and,
l = Slant height
List of Geometry Formulas
Geometry Formulas from Class 8 to 12
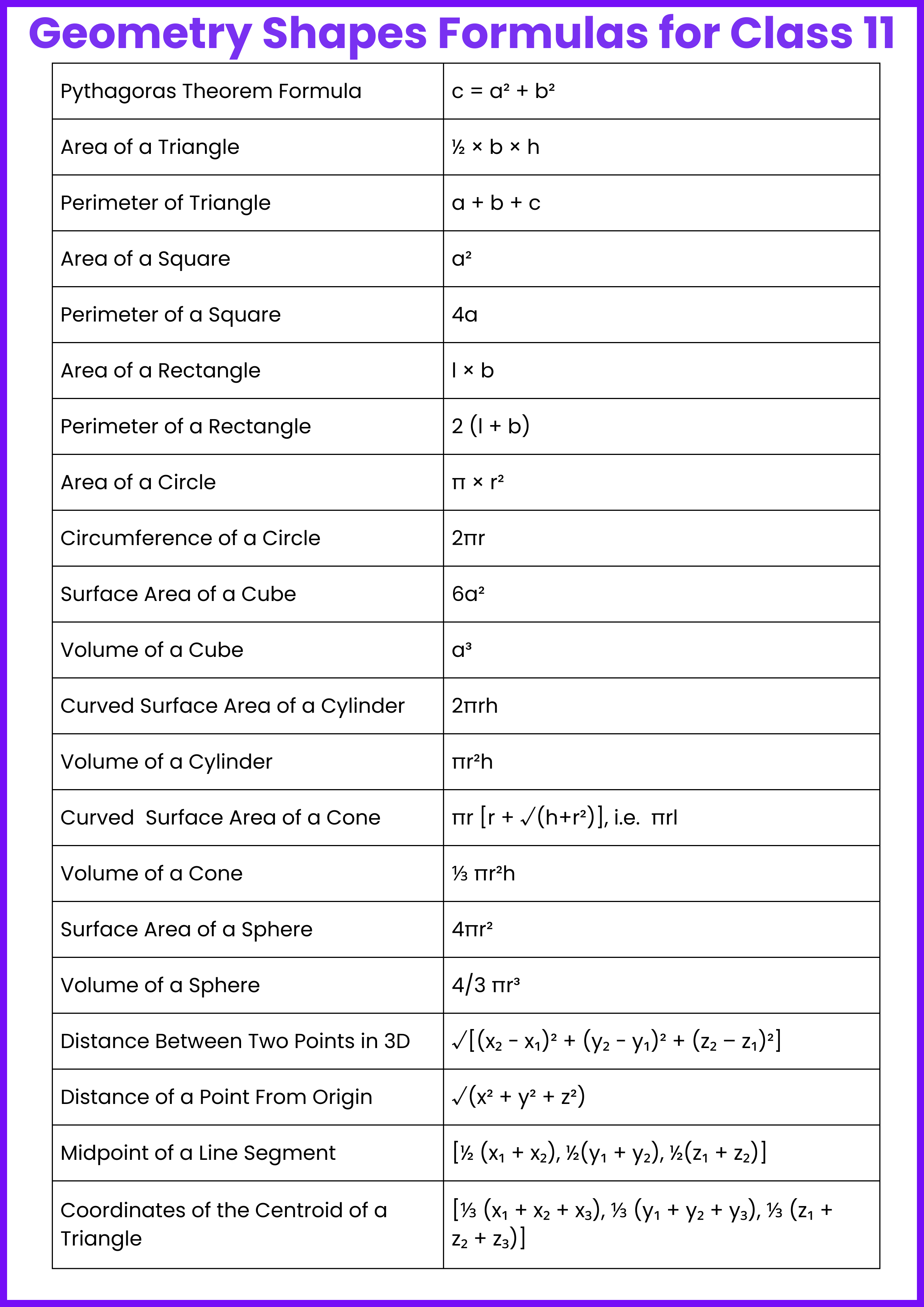
From Class 8 to12, geometry formulas evolve from basic to advanced concepts. In Class 8, students learn foundational formulas for area, perimeter, and volume of simple shapes like rectangles, triangles, and circles. By Class 12, the curriculum includes more complex formulas involving 3D shapes, vectors, trigonometry, and coordinate geometry, preparing students for higher-level mathematics and practical applications in various fields.
Download Geometry Formulas from Class 8 to 12 PDF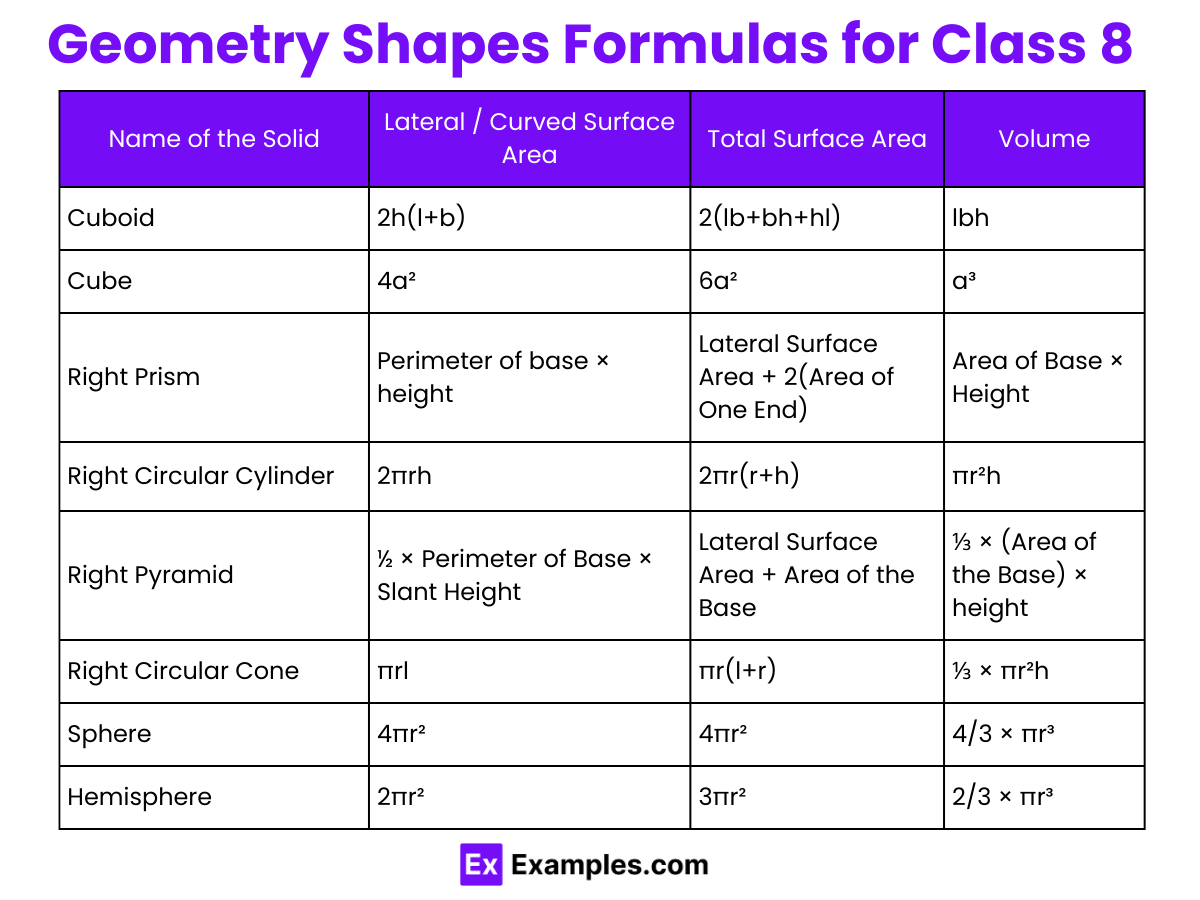Geometry Formulas For Class 8
Geometry Formulas For Class 9
Geometry Formulas For Class 10
Geometry Formulas For Class 11
Geometry Formulas For Class 12
FAQs
Is geometry harder than algebra?
The difficulty of geometry versus algebra varies by individual. Some find geometry’s visual and spatial reasoning easier, while others prefer algebra’s symbolic manipulation. Personal strengths and learning styles significantly impact which subject feels more challenging.
Is geometry in 7th grade?
Yes, geometry is typically introduced in 7th grade. Students learn about basic geometric shapes, angles, area, perimeter, and volume. This foundational knowledge prepares them for more advanced geometry in higher grades.
How hard is geometry?
Geometry’s difficulty depends on the student’s spatial reasoning and ability to visualize shapes. While some find it intuitive, others may struggle with concepts like proofs and theorems. Practice and a solid understanding of foundational principles can ease the learning process.
Who is the father of geometry?
Euclid is often referred to as the “Father of Geometry.” His work, “Elements,” laid the foundational principles and axioms of geometry that are still used today. Euclid’s systematic approach significantly shaped the study of mathematics.
What does 𝑝 mean in math geometry?
In geometry, p commonly denotes the perimeter of a shape. For example, 𝑝p might represent the total length around a polygon. It is used in various formulas, such as p=2(l+w) for the perimeter of a rectangle.
What is the most basic geometry?
The most basic geometry deals with simple shapes and their properties, such as points, lines, angles, triangles, and circles. Fundamental concepts include measuring angles, calculating area and perimeter, and understanding basic properties of geometric figures.
How many basic terms are there in geometry?
There are several basic terms in geometry, including points, lines, planes, angles, segments, and rays. These foundational concepts form the building blocks of more complex geometric principles and theorems. Understanding these terms is crucial for studying geometry.
Share :
Practice Test
What is the circumference of a circle with a radius of 7 cm?
43.96 cm
44.96 cm
45.96 cm
46.96 cm
of 10
What is the volume of a cube with a side length of 4 cm?
64 cm³
74 cm³
84 cm³
94 cm³
of 10
What is the area of a rectangle with a length of 10 cm and a width of 6 cm?
50 cm²
55 cm²
60 cm²
65 cm²
of 10
What is the surface area of a sphere with a radius of 3 cm?
113.04 cm²
123.04 cm²
133.04 cm²
143.04 cm²
of 10
What is the volume of a cylinder with a radius of 3 cm and a height of 7 cm?
197.82 cm³
207.82 cm³
217.82 cm³
227.82 cm³
of 10
What is the perimeter of a rectangle with a length of 12 cm and a width of 8 cm?
30 cm
35 cm
40 cm
45 cm
of 10
What is the area of a parallelogram with a base of 9 cm and a height of 4 cm?
32 cm²
34 cm²
35 cm²
36 cm²
of 10
What is the surface area of a cube with a side length of 5 cm?
125 cm²
150 cm²
175 cm²
185 cm²
of 10
What is the volume of a cone with a radius of 4 cm and a height of 9 cm?
120.32 cm³
130.32 cm³
140.32 cm³
150.32 cm³
of 10