What is the prime factorization of 30?
2 × 3 × 5
2 × 3 × 6
2 × 5
3 × 10


Prime factorization, the process of breaking down a number into the set of prime numbers that multiply together to result in the original number, is a cornerstone of number theory. Through engaging examples and clear, concise explanations, this guide aims to demystify the process, showcasing its practicality and importance in various mathematical applications, from solving greatest common divisor (GCD) problems to simplifying fractions. Whether you’re tackling homework problems or exploring mathematical theories, mastering prime factorization is a skill that enhances both academic and real-world mathematical proficiency.
Prime factorization is the method of expressing a number as the product of its prime factors. This fundamental concept in mathematics involves breaking down a composite number into a combination of prime numbers that, when multiplied together, give back the original number. For example, the prime factorization of 12 is 2 x 2 x 3, indicating that when the prime numbers 2 and 3 are multiplied together in this manner, the result is 12. Understanding prime factorization is crucial for various mathematical operations, including simplifying fractions and finding the least common multiple (LCM) or greatest common divisor (GCD) of two numbers. It’s a key skill that enhances one’s ability to work with numbers and solve a wide range of mathematical problems.
Here are several examples of prime factorization, demonstrating how to break down composite numbers into their prime factors:
| Numbers | Prime Factorization |
|---|---|
| 90 | 2×32×5 |
| 100 | 22×52 |
| 84 | 22×3×7 |
| 96 | 25×3 |
| 108 | 22×33 |
| 64 | 26 |
| 75 | 3×52 |
| 80 | 24×5 |
| 125 | 53 |
| 99 | 32×11 |
| 120 | 23×3×5 |
There are various methods for the prime factorization of a number. The most common methods that are used for prime factorization are given below:
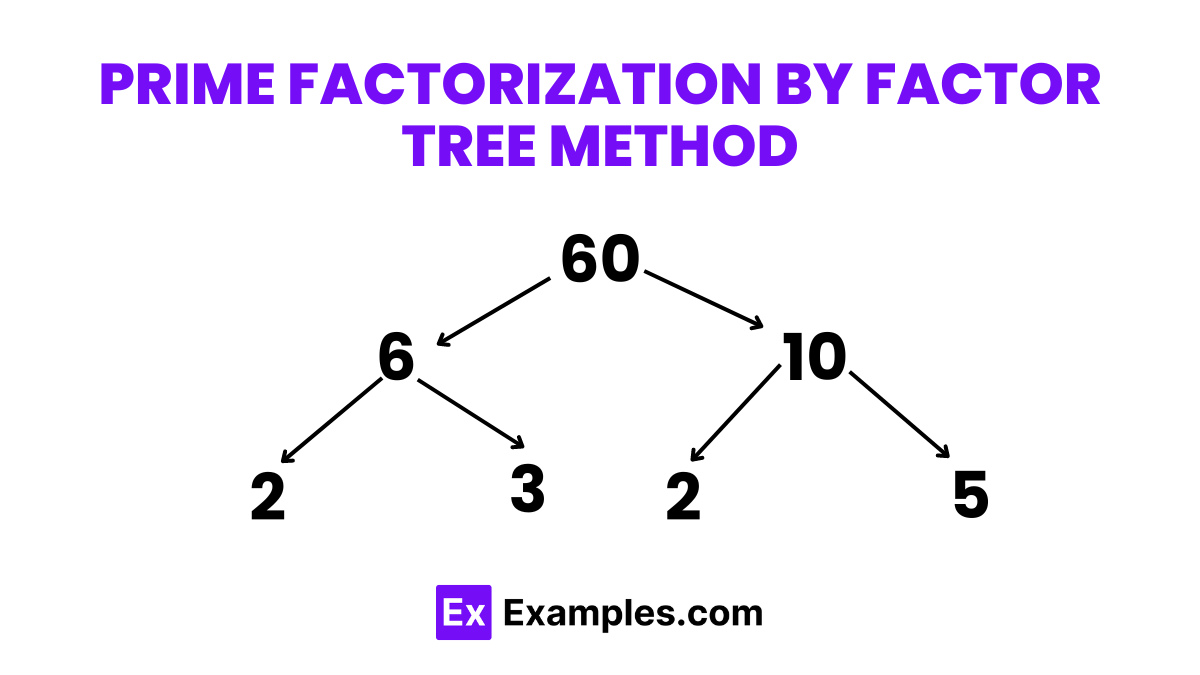
The factor tree method involves breaking down a number into its prime factors by creating a tree diagram. Each branch of the tree splits the number into factors, continuing until all branches end in prime numbers.
Example: Factorize 60 using the factor tree method.
Solution Steps:
The division method for prime factorization involves dividing the number by the smallest possible prime number (2, 3, 5, etc.) until the result is 1. At each step, the divisor that results in a whole number is a prime factor.
Example: Factorize 60 using the division method.
Solution Steps:
These methods offer systematic ways to break down a number into its prime components, each providing a clear pathway through either visual representation or sequential division to arrive at the prime factorization of a number.
Prime factorization, the process of breaking down a number into its prime number components, serves as a cornerstone in mathematics with broad applications. It is crucial for simplifying fractions, finding the greatest common divisors (GCD), least common multiples (LCM), and solving Diophantine equations.
Example: Simplifying the fraction 8/12 involves prime factorizing the numerator (8 = 2 x 2 x 2) and the denominator (12 = 2 x 2 x 3), leading to its simplest form 2/3 by canceling common factors.
The HCF or GCD of two numbers is the highest number that divides both of them without leaving a remainder.
Steps with Example:
The LCM of two numbers is the smallest number that is a multiple of both.
Steps with Example:
These methods of using prime factorization to find HCF and LCM showcase its practical utility in solving problems that require understanding the fundamental structure of numbers.
It’s crucial for various mathematical applications, including simplifying fractions, finding the greatest common divisors (GCD), least common multiples (LCM), and solving problems in number theory.
Every composite number can be prime factorized. However, prime numbers and the number 1 are exceptions; prime numbers are their own prime factors, and 1 is not considered because it does not meet the definition of a prime number.
To find the prime factorization of a number, divide the number by the smallest prime number (2) and continue dividing by prime numbers (3, 5, 7, etc.) until the quotient is a prime number.
Prime numbers are natural numbers greater than 1 that have no divisors other than 1 and themselves. Prime factors are prime numbers that multiply together to give a composite number.
No, 1 is not considered a prime factor because it does not meet the definition of a prime number, which must have exactly two distinct positive divisors.
No, the Fundamental Theorem of Arithmetic states that every integer greater than 1 either is prime itself or can be uniquely represented as a product of prime numbers, up to the order of the factors.
Prime factorization helps identify common factors in the numerator and denominator of a fraction, allowing them to be cancelled out to simplify the fraction to its lowest terms.
In cryptography, prime factorization is used in algorithms for public key encryption, where large prime numbers and their products are fundamental to the security of encrypted data.
While there are algorithms that can perform prime factorization more efficiently than trial division, such as the Sieve of Eratosthenes for finding primes or the Pollard Rho algorithm for factorization, prime factorization of very large numbers remains computationally challenging, which is a basis for the security of many encryption systems.
Prime factorization is a fundamental mathematical process that breaks down composite numbers into their prime components. It’s essential for simplifying fractions, calculating GCD and LCM, and has significant applications in number theory and cryptography. Understanding prime factorization enriches one’s mathematical skills, offering a deeper insight into the structure of numbers and their properties, and highlighting its indispensable role in both academic and practical mathematics.
Text prompt
Add Tone
Prime Factorization of a Number
Methods of Prime Factorization
What is the prime factorization of 30?
2 × 3 × 5
2 × 3 × 6
2 × 5
3 × 10
What is the prime factorization of 56?
2 × 2 × 2 × 7
2 × 2 × 2 × 4 × 7
2 × 2 × 2 × 2 × 7
2 × 2 × 7
What is the prime factorization of 36?
2 × 3 × 6
2 × 2 × 3 × 3
2 × 2 × 3
2 × 2 × 3 × 6
Find the prime factorization of 81.
3 × 3 × 3 × 3
3 × 3 × 9
2 × 2 × 3 × 3 × 3
3 × 3 × 3
What is the prime factorization of 45?
3 × 3 × 5
2 × 3 × 5
3 × 5
3 × 3 × 3 × 5
What is the prime factorization of 100?
2 × 2 × 2 × 5 × 5
2 × 2 × 5 × 5
2 × 2 × 2 × 2 × 5
2 × 2 × 2 × 5
Find the prime factorization of 120.
2 × 2 × 2 × 3 × 5
2 × 2 × 3 × 4 × 5
2 × 2 × 2 × 3 × 3 × 5
2 × 2 × 3 × 5
What is the prime factorization of 72?
2 × 2 × 2 × 2 × 3
2 × 2 × 2 × 3 × 3
2 × 2 × 3 × 3
2 × 3 × 3 × 3
Find the prime factorization of 64.
2 × 2 × 2 × 2 × 4
2 × 2 × 2 × 4 × 4
2 × 2 × 2 × 2 × 2 × 2
2 × 2 × 2 × 2 × 2
Find the prime factorization of 81.
3 × 3 × 3 × 3
3 × 3 × 3
2 × 3 × 3 × 3
3 × 3 × 3 × 2
Before you leave, take our quick quiz to enhance your learning!

