Which of the following numbers is a prime number?
390
41
45
51


Prime numbers up to 100 are natural numbers greater than 1 that have no positive divisors other than 1 and themselves, making them indivisible by any other number except for these two. These numbers include 2, 3, 5, 7, and continue up to 97. A total of 25 prime numbers exist within this range, each playing a crucial role in number theory and various applications in mathematics. The unique property of prime numbers is their inability to be expressed as a product of smaller natural numbers, setting them apart from composite numbers. Understanding prime numbers up to 100 is foundational for studying more complex mathematical concepts and their practical uses.
Download Prime Numbers upto 100
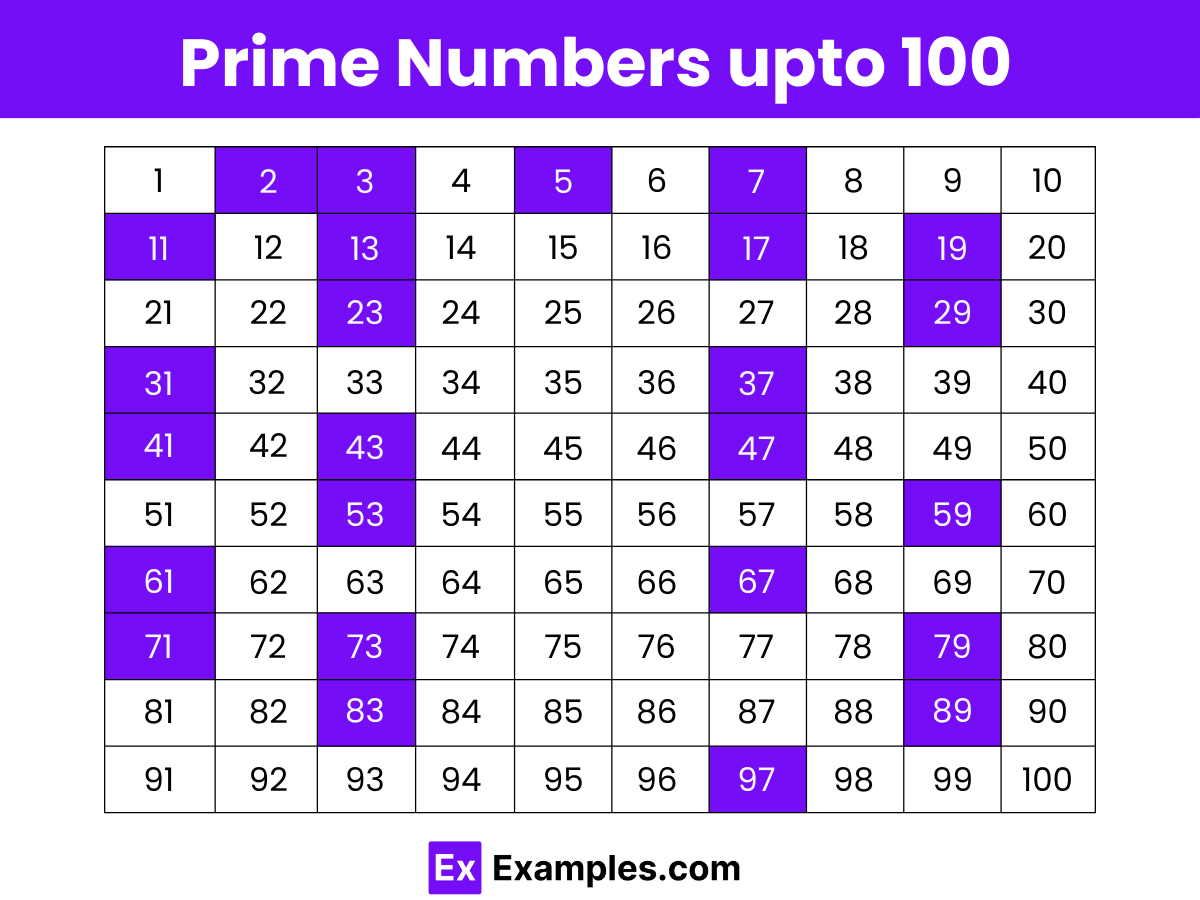
Download Prime Numbers upto 100
| Prime Numbers | Prime Numbers |
|---|---|
| 2 | 43 |
| 3 | 47 |
| 5 | 53 |
| 7 | 59 |
| 11 | 61 |
| 13 | 67 |
| 17 | 71 |
| 19 | 73 |
| 23 | 79 |
| 29 | 83 |
| 31 | 89 |
| 37 | 97 |
| 41 |
Understanding prime numbers up to 100 is fundamental to grasping more complex mathematical concepts. These numbers, including notable examples like 2, 3, 5, 7, 11, 13, and so forth up to 97, serve as the building blocks in number theory. They are essential in various mathematical applications, including cryptography, computer algorithms, and prime factorization. By studying the prime numbers up to 100, students and mathematicians can gain a deeper appreciation of their unique properties and their critical role in the structure of numbers. This foundational knowledge paves the way for exploring more advanced topics and practical uses of primes in science and technology.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
Which of the following numbers is a prime number?
390
41
45
51
Identify the prime number among these:
49
53
55
57
What is the prime number in this list?
62
67
70
74
Which of these is not a prime number?
73
77
79
83
Find the prime number in the following options:
89
91
93
95
Which number is a prime number?
94
97
99
100
Select the prime number from the following:
33
37
39
45
What is the prime number in this set?
46
53
55
58
Which of these numbers is a prime number?
63
67
69
72
Identify the prime number from this list:
76
79
82
88
Before you leave, take our quick quiz to enhance your learning!

