Scientific notation
Scientific notation
What is Scientific notation ?
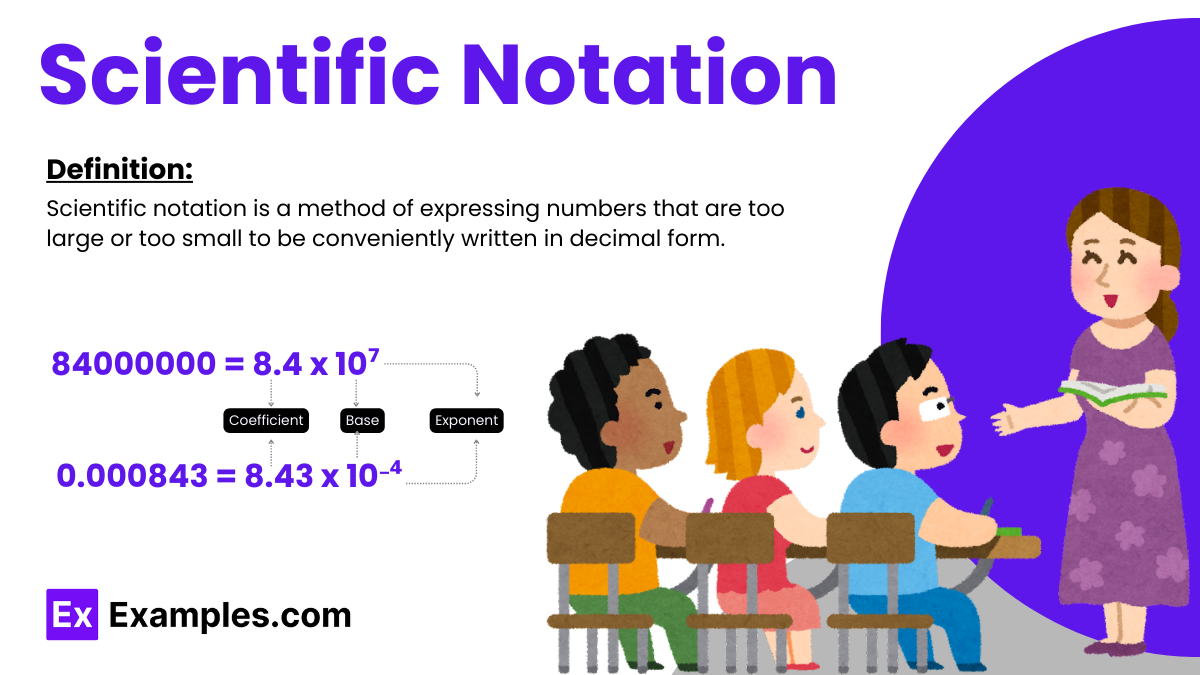
Scientific notation is a method of expressing numbers that are too large or too small to be conveniently written in decimal form. It is often used in science, engineering, and mathematics to make calculations with very large or very small numbers more manageable
Scientific Notation Rules
- The base should be always 10
- The exponent must be a non-zero integer, that means it can be either positive or negative
- The absolute value of the coefficient is greater than or equal to 1 but it should be less than 10
- Coefficients can be positive or negative numbers including whole and decimal numbers
- The mantissa carries the rest of the significant digits of the number
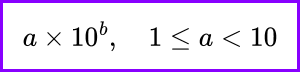
The general representation of scientific notation is:
Scientific Notation Examples
The examples of scientific notation are:
590000000 = 5.9×108
7230000000 = 7.23×109
90500000 = 9.05 x 107
0.000000047 = 4.7 x 10-8
0.0000315 = 3.15 x 10-5
Positive and Negative Exponent
Scientific notation with positive and negative exponents is a versatile way to express a wide range of numbers, from very large to very small. Here’s how these exponents function within the context of scientific notation:
Positive Exponents
In scientific notation, a positive exponent indicates a number greater than 1. The exponent tells us how many times to multiply the number by ten. For example:
- 3.2×10³ represents 3.2 multiplied by 10 three times, or 3200
- 1.5×10⁵ means 1.5 multiplied by 10 five times, resulting in 150000.
These are typically used to represent large numbers such as distances in astronomy, large amounts of data in bytes, or other significant quantities.
Negative Exponents
Conversely, a negative exponent signifies a number less than 1. This exponent denotes how many times the number is divided by ten. For instance:
- 4.7×10−² equals 4.7divided by 100, or 0.047
- 6.3×10⁻⁴ translates to 6.3 divided by 10,000 resulting in 0.00063
Negative exponents are common when dealing with microscopic scales, such as the sizes of bacteria, wavelengths of light in certain parts of the spectrum, or small time intervals
FAQs
How is 6.3 written in scientific notation?
6.3 is already in a form suitable for scientific notation as 6.3×10⁰ , where the exponent indicates that the decimal point has not moved..
How to write scientific notation e?
In contexts involving e (Euler’s number), scientific notation uses “e” to denote powers of ten, as in 1.2e3 for 1.2 x 10³
How to convert scientific notation to standard notation?
To convert from scientific to standard notation, shift the decimal point in the coefficient right for positive exponents or left for negative exponents by the value of the exponent.
What is scientific notation for 7th grade?
For 7th graders, scientific notation is a way to write very large or small numbers using a coefficient between 1 and 10 multiplied by a power of ten.
What is 10000000000 in scientific notation?
The number 10,000,000,000 is written in scientific notation as 1×10¹⁰
What does e mean in math?
In mathematics, e typically represents Euler’s number, approximately 2.718, which is the base of natural logarithms, used in continuous growth or decay processes.
What are the 3 steps to scientific notation?
The three steps are: 1) Move the decimal point in the number to create a new number from 1 up to 10; 2) Count the number of places the decimal moved; 3) Write as a product of the new number and 10 raised to the count.
What’s 10 raised to the power?
“10 raised to the power” refers to exponential notation where 10 is multiplied by itself a specified number of times, such as 10³=1000.
Can a negative number be written in scientific notation?
Yes, a negative number can be written in scientific notation by placing a minus sign before the coefficient, e.g.,−3.4×10²
Share :
