Calculate the square root of 16 divided by the square root of 4.
1
2
3
4
of 10
Square & Square Root of 4 – Methods, Calculation, Formula, How to find
Square of 4
To calculate the square of 4, you simply multiply 4 by itself:
The square of 8, denoted as 4², is the result of multiplying the number 8 by itself. In mathematical terms, So, the square of 4 is 16. Geometrically, this means that if you have a square with each side measuring 6 units, the total area enclosed by the square will be 16 square units.
Square Root of 4
The square root of 4, denoted as √4, is a number that, when multiplied by itself, equals 4. In mathematical terms, So, the square root of 4 is 2. This is because 2 multiplied by itself equals 4.In geometric terms, the square root of 4 represents the length of each side of a square with an area of 4 square units.
It is a fundamental concept in mathematics and serves as a building block for understanding more complex mathematical operations and concepts. It’s one of the simplest square roots and is used extensively in various mathematical calculations and problem-solving scenarios.
Exponential Form: 4^½ or 4^0.5
Radical Form: √2
Is the Square Root of 4 Rational or Irrational?
The square root of 4 (√4) is equal to 2. Since 2 can be expressed as the ratio of two integers (2/1), where both 2 and 1 are integers and the denominator is not zero, √4 is classified as a rational number.
- A rational number is any number that can be expressed as the quotient or fraction of two integers. In the case of √4, it fits this definition because it can be written as a fraction with both the numerator and denominator being integers.
- An irrational number is a real number that cannot be expressed as a simple fraction or ratio of two integers. However, the square root of 4 is exactly 2.
- A rational number is any number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In other words, rational numbers can be written as a simple fraction.
Method to Find Value of Root 4
- Mental Calculation: Since the square root of 4 is a well-known value, you can mentally recognize that the square root of 4 is 2. This method is quick and straightforward, suitable for simple calculations.
- Calculator: Use a calculator to directly calculate the square root of 4. Most calculators have a square root function, allowing you to input 4 and calculate its square root, which will give you the result of 2.
- Newton’s Method: Newton’s method is an iterative algorithm for finding the roots of a real-valued function. While it’s more complex, it can be used to find square roots, including the square root of 4.
Square Root of 4 by Long Division Method
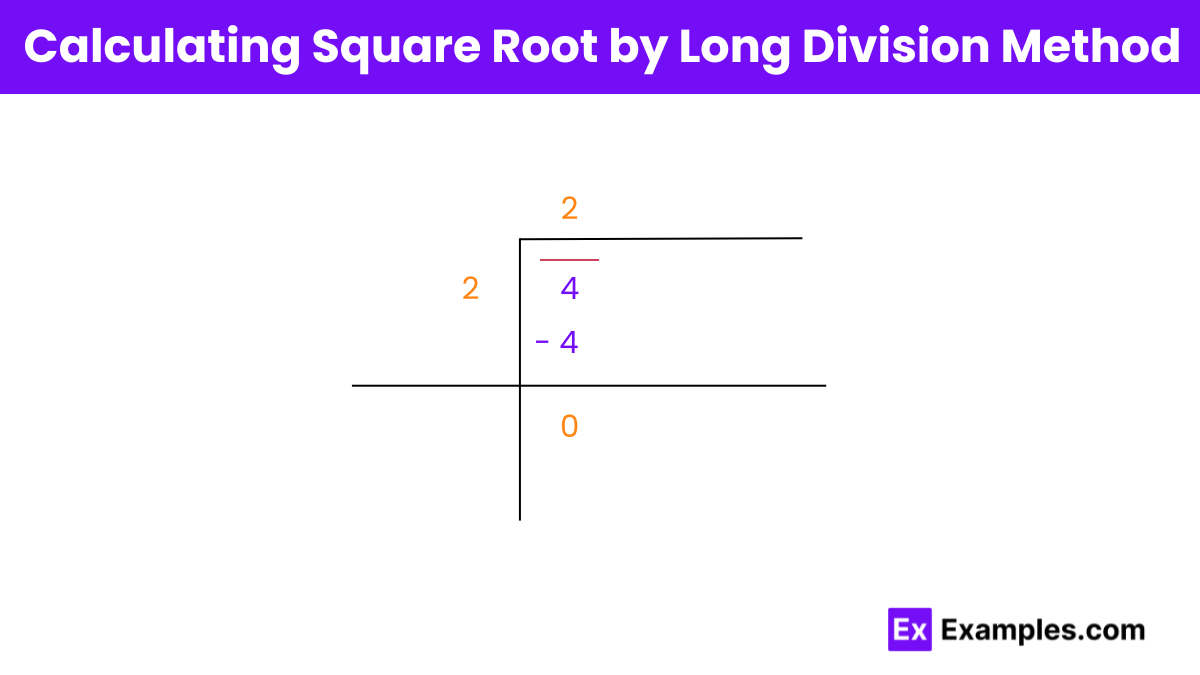
Square Root of 4 (√4):
- Recognize the operation: Understand that finding the square root of a number involves determining the number that, when multiplied by itself, equals the original number.
- Compute: Calculate the square root of 4. Since 2×2 = 4, the square root of 4 is 2.
- Interpretation: This means that the length of each side of a square with an area of 4 square units is 2 units.
- Check: Verify the result by squaring the calculated square root. In this case, 2×2 = 4, confirming that the square root of 4 is indeed 2.
4 is Perfect Square root or Not
A perfect square is a number that can be expressed as the product of an integer multiplied by itself. In other words, it is the square of an integer.
Since 2×2 = 4, 4 can be expressed as the square of the integer 2. Therefore, 4 is indeed a perfect square.
FAQ’s
What is the significance of the square root of 4?
The square root of 4 is significant in mathematics as it represents the length of each side of a square with an area of 4 square units. It is also used in various calculations, such as finding side lengths, solving equations, and determining geometric properties.
Can the square root of 4 be simplified further?
No, the square root of 4 cannot be simplified further because it is already in its simplest form as 2.
What are some practical applications of the square root of 4?
The square root of 4 has practical applications in fields such as geometry, physics, engineering, and finance. It is used to calculate dimensions, distances, areas, and volumes in various real-world scenarios.
Share :
Practice Test
What is the square root of 4 multiplied by 3?
6
7
8
9
of 10
Find the number whose square root is 2.
2
4
8
16
of 10
What is the square of 4?
8
12
16
21
of 10
Find the square root of 4.
0
1
2
3
of 10
What is 4 raised to the power of 2?
8
12
16
20
of 10
If x² = 4, what are the possible values of x?
2
-2
2 and -2
4
of 10
What is the result of 4 squared minus the square root of 4?
12
14
16
18
of 10
What is the difference between the square of 4 and the square root of 4?
12
14
16
18
of 10
If a number squared is 4, what is that number?
1
2 or -2
3
5
of 10