Square & Square Root of 48

Square 48

The “square of 48” represents the outcome when the number 48 is multiplied by itself.

In mathematical notation, it’s denoted as 48². To compute the square of 48, you multiply 48 by 48, resulting in 2304.

Mathematically, 48² (48 × 48) = 2304

Calculating the square of 48 entails straightforward arithmetic, involving the multiplication of 48 by itself. This calculation is frequently encountered in various mathematical contexts, notably in geometry and algebra.

Square Root of 48

√48 = 6.928203230275509

    or

√48 ≈ 6.928 up to three decimal places

The square root of 48, denoted as √48, is a fundamental mathematical concept representing the value that, when multiplied by itself, equals 48. Similar to the square root of 40, the square root of 48 is also an irrational number, implying its decimal expansion is non-repeating and infinite. When approximated, the value of √48 is approximately 6.928203230275509. Despite its seemingly unpredictable decimal expansion, the square root of 48 plays a crucial role in various mathematical calculations, geometric analyses, and practical applications. Understanding this concept aids in problem-solving across disciplines like engineering, physics, and finance.

Square Root of 48: 6.928203230275509

Exponential Form: 48^½ or 48^0.5

Radical Form: √48

Is the Square Root of 48 Rational or Irrational?

The square root of 48 is an irrational number

To understand why, let’s first define rational and irrational numbers.

Rational numbers are those expressible as a fraction of two integers, where the denominator is not zero, written as a/b.

Examples include 1/2, -3, and 5.

Irrational numbers, however, cannot be expressed as simple fractions of two integers. Their decimal representations are non-repeating and non-terminating.

Examples include √2, π (pi), and √3.

Square Root of 48 as Irrational:

When we calculate the square root of 48, we find it cannot be expressed as a fraction of two integers.

Its decimal expansion, approximately 6.928203230275509, continues infinitely without repeating a pattern.

Let’s simplify:

√48 = √(16 × 3) = √16 × √3 = 4 × √3

Since √3 is famously irrational, the product of a rational number (4) and an irrational number (√3) is also irrational.

In summary, the square root of 48 is irrational because it simplifies to an irrational number (√3) when multiplied by a rational number (4), resulting in an irrational product.

Method to Find Value of Root 48

Finding the square root of a number can be done through various methods. Here are some common approaches to determine the value of the square root of 48:

1. Prime Factorization Method:
   • Decompose 48 into its prime factors: 2 × 2 × 2 × 2 × 3.
   • Group the prime factors: √(2 × 2 × 2 × 2 × 3).
   • Since 48 contains perfect square factors, simplify to obtain the square root in radical form.
2. Long Division Method:
   • Start with an initial approximation for the square root of 48.
   • Iteratively refine the approximation through successive long divisions.
   • Continue adjusting the approximation until achieving the desired level of accuracy.
3. Estimation Method:
   • Recognize that 48 is near the square of a whole number.
   • Identify nearby perfect squares: 36 (6²) and 49 (7²).
   • Since 48 lies between 36 and 49, estimate its square root to be between 6 and 7.
4. Babylonian Method(Heron’s Method):
   • Initiate with a tentative guess for the square root of 48, such as 6.
   • Utilize the Babylonian formula: xₙ₊₁=1/2(xₙ+40/xₙ) to iteratively enhance the guess.
   • Continue the iterations until reaching the desired precision level.

These methods furnish clear strategies for calculating the value of the square root of 48, accommodating various skill levels and preferences in mathematical reasoning.

Square Root of 48 by Prime Factorization Method

The prime factorization method is a technique used to find the square root of a number by breaking it down into its prime factors. Here’s how to calculate the square root of 48 using this method:

1. Decompose 48 into its Prime Factors: Start by identifying the prime factors of 48. In the case of 48, it can be broken down into 2 × 2 × 2 × 2 × 3.
2. Group the Prime Factors: Arrange the prime factors in pairs. For 48, we have √(2 × 2 × 2 × 2 × 3).
3. Simplify: Since 48 contains perfect square factors (2 × 2), we can simplify the expression to obtain the square root in radical form. This simplification results in 4√3.

By following these steps, we can determine that the square root of 48 by prime factorization method is 4√3. This method provides a systematic approach to finding square roots and is particularly useful when dealing with larger numbers.

Square Root of 48 by Long Division Method

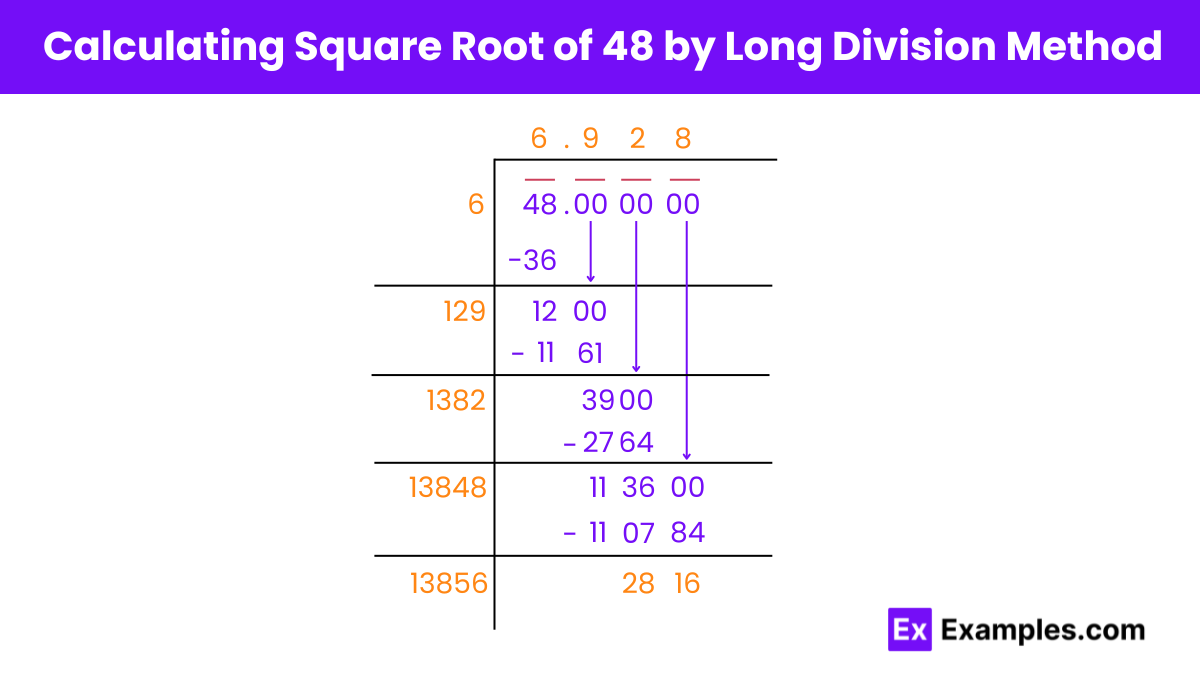
Here’s a step-by-step guide to finding the square root of 48 using the long division method:

Step 1: Identify the largest perfect square less than 48, which is 6 since 6²=36.

Step 2: Subtract 36 from 48 to get a remainder of 12.

Step 3: Double the initial quotient of 6 to get 12.

Step 4: Bring down two zeros next to the remainder to get 1200. Find a digit that, when appended to 12 and multiplied by the same digit, results in a product just below 1200. If 129×9=1161, subtract this from 1200 to get a remainder of 39.

Step 5: Bring down another pair of zeros to make the remainder 3900. Adjust the base from Step 3 to 138 (adding the last digit used, 9, to 129) and find a digit such that 138 x × x is just less than 3900. If 1382×2=2764, subtract this from 3900 to get a remainder of 1136.

Step 6: Continue as in the previous example until the desired level of accuracy is reached. The square root of 48, calculated to two decimal places, should be approximately 6.928.

Following these steps systematically allows us to approximate the square root of 48 using the long division method.

FAQ’s

Is the Square Root of 48 a Natural Number?

No, the square root of 48 is not a natural number. Natural numbers are the set of positive integers starting from 1 (1, 2, 3, 4, …). The square root of 48 is approximately 6.9282, which is not a whole number and therefore cannot be classified as a natural number.

Is the Square Root of 48 a Perfect Square?

No, the square root of 48 is not a perfect square. A perfect square is an integer that is the square of another integer. Since the square root of 48 is not an integer (as explained above), 48 itself cannot be a perfect square. The numbers close to 48 that are perfect squares are 36 (6^2) and 49 (7^2).

What Square Root is Between 48?

The square root of 48 is between two consecutive whole numbers. To find the integers between which the square root of 48 lies, we can determine the squares of consecutive integers:

5² = 25

6² = 36

7² = 49

Since 48 lies between 36 and 49, the square root of 48 is between 6 and 7. Specifically, it is approximately 6.928.