Square Numbers

Square numbers, also known as perfect squares, are integers that can be expressed as the product of an integer with itself. This characteristic yields a distinct pattern of numbers, such as 1, 4, 9, 16, and so on. These numbers hold a significant place in mathematics due to their symmetrical properties and their role in various mathematical operations and theorems.

Square Number: Definition

A square number can be defined as the positive integer obtained by multiplying an integer with itself.Square numbers are fundamental in mathematics, illustrating concepts of area and forming the basis of more complex mathematical discussions

What Is a Square Number in Math?

A square number is a number obtained when an integer is multiplied by itself.And It is also referred to as “a perfect square.”

Multiplying two positive integers together yields a positive result. And similarly, when two negative integers are multiplied, the outcome is also positive.

(+) × (+) = (+)

(-) × (-) = (+)

Examples of square numbers:

4 × 4 =16

(-5) × (-5) =  25

How to find Square Numbers ?

square numbers involves a simple process based on the definition of what a square number is. A square number, or a perfect square, is the product of an integer multiplied by itself. Here’s how you can find square numbers:

1. Choose an Integer: Select any integer. This could be a positive number, a negative number, or zero.
2. Multiply the Integer by Itself: Use the multiplication operation to multiply the chosen integer by itself. The formula for this is N², where $N$ is the integer you’ve chosen.
3. Result: The result of this multiplication is a square number. For instance, if you select 4 as your integer, multiplying 4 by itself (i.e., 4×4 or 4²) gives you 16, which is a square number.

Examples:

• $²=$
• $²=$
• $²=$
• $²=$

Properties of Square Numbers

1. Last Digit Characteristics: Only the numerals 0, 1, 4, 5, 6, or 9 can appear as the final digit in square numbers, excluding those ending in 2, 3, 7, or 8 from being perfect squares.
2. Ending Zeros in Squares: Perfect squares must feature zeros in pairs at their conclusion, disqualifying numbers with a solitary or odd tally of zeros at the end, such as 20, 360, or 480, unlike valid squares like 900 and 4900.
3. Outcome of Squaring Specific End Digits: Numbers concluding in 1 or 9 yield squares that terminate in 1, whereas those ending in 4 or 6 result in squares concluding in 6.
4. Parity of Square Numbers: The square of an even numeral remains even, and conversely, squaring an odd number produces an odd result, affirming the non-negative nature of square numbers.
5. Positivity of Squares: The nature of squaring ensures all square numbers manifest as positive values.
6. Criteria for Perfect Squares: A numerical value whose square root emerges as a fraction or a decimal is not recognized as a perfect square, exemplified by the fact that 0.25 does not qualify as a square number.

List of Square Numbers (1 to 100)

Download This Image

Number – Square	Number – Square	Number – Square	Number – Square	Number – Square
1$²=$ 1	21$²=$441	41$²=$1681	61$²=$3721	81$²=$6561
2$²=$4	22$²=$484	42$²=$1764	62$²=$3844	82$²=$6724
3$²=$9	23$²=$529	43$²=$1849	63$²=$3969	83$²=$6889
4$²=$16	24$²=$576	44$²=$1936	64$²=$4096	84$²=$7056
5$²=$25	25$²=$625	45$²=$2025	65$²=$4225	85$²=$7225
6$²=$36	26$²=$676	46$²=$2116	66$²=$4356	86$²=$7396
7$²=$49	27$²=$729	47$²=$2209	67$²=$4489	87$²=$7569
8$²=$64	28$²=$784	48$²=$2304	68$²=$4624	88$²=$7744
9$²=$81	29$²=$841	49$²=$2401	69$²=$4761	89$²=$7921
10$²=$100	30$²=$900	50$²=$2500	70$²=$4900	90$²=$8100
11$²=$121	31$²=$961	51$²=$2601	71$²=$5041	91$²=$8281
12$²=$144	32$²=$1024	52$²=$2704	72$²=$5184	92$²=$8464
13$²=$169	33$²=$1089	53$²=$2809	73$²=$5329	93$²=$8649
14$²=$196	34$²=$1156	54$²=$2916	74$²=$5476	94$²=$8836
15$²=$225	35$²=$1225	55$²=$3025	75$²=$5625	95$²=$9025
16$²=$256	36$²=$1296	56$²=$3136	76$²=$5776	96$²=$9216
17$²=$289	37$²=$1369	57$²=$3249	77$²=$5929	97$²=$9409
18$²=$324	38$²=$1444	58$²=$3364	78$²=$6084	98$²=$9604
19$²=$361	39$²=$1521	59$²=$3481	79$²=$6241	99$²=$9801
20$²=$400	40$²=$1600	60$²=$3600	80$²=$6400	100$²=$10000

Two-digit Square Numbers

Two-digit square numbers are the squares of integers that result in values between 10 and 99.

• 4²=16
• 5²=25
• $²$
• $²$
• $²$
• $²$

Three-digit Square Numbers

• 10²=100
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$
• $²=$

Odd and Even Square Numbers

• Even Square Numbers: When an even number is squared (e.g,$2,4,6,\dots$), the result is always an even square number. This is because the multiplication of any two even numbers (and squaring an even number is essentially multiplying it by itself) will always result in an even number. For example, $²$ and $²$ are both even square numbers.
• Odd Square Numbers: Conversely, when an odd number is squared (e.g., 1,3,5,…), the result is always an odd square number. This occurs because the product of any two odd numbers remains odd. For instance, $²$and $²$ are odd square numbers.

Square Numbers and Multiplication Arrays

Download This Image

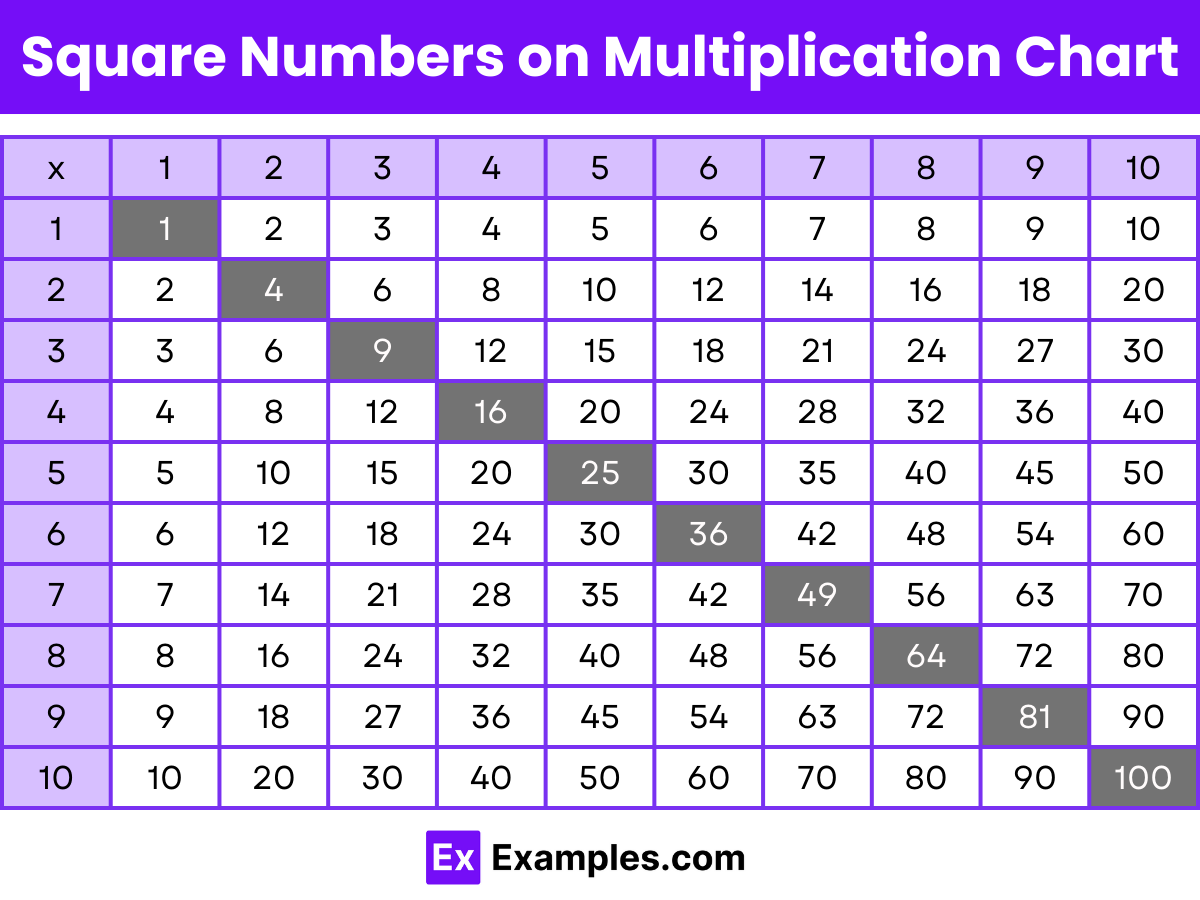
x	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Facts about Square Numbers

1. Square of a Sum: The square of the sum of two numbers can be expanded as (a+b)²=a²+2ab+b². This formula is a cornerstone in algebra, illustrating how two quantities, when squared together, yield not just their individual squares but also a combined term.
2. Square of a Difference: Similarly, the square of the difference between two numbers is expressed as (a−b)²=a²−2ab+b². This highlights the symmetrical nature of algebraic operations, even when dealing with subtraction.
3. Difference of Squares: A powerful algebraic identity is the difference of squares a²−b²=(a+b)(a−b). This shows that the difference between any two square numbers can be factored into a product of their sum and difference.
4. Pythagorean Theorem: In algebra, square numbers play a crucial role in the Pythagorean theorem, a²+b²=c², where $c$ is the hypotenuse of a right triangle, and $a$ and $b$ are the other two sides. This theorem is a practical application of square numbers in geometry.
5. Perfect Square Trinomials: Algebra introduces the concept of perfect square trinomials, expressions that can be factored into the square of a binomial. For example, x²+2xy+y² can be factored as (x+y)², showcasing how algebraic expressions can represent square numbers.
6. Square Root Function: The square root function, denoted as √x​, is fundamental in algebra for finding the original number that was squared. This function highlights the inverse relationship between squaring and finding a square root.
7. Integral Solutions: Square numbers are integral in solving quadratic equations, where the solution involves finding the square root of a number. This can lead to integral or real solutions, depending on the discriminant.
8. Sum of Consecutive Odd Numbers: Algebraically, it can be shown that any square number is the sum of consecutive odd numbers starting from 1, a property that illustrates the progressive addition of layers to form squares.

Practice Problems

Problem 1: Statistical Sum of Squares

Given a dataset: 4, 8, 12. Calculate the sum of squares for this dataset.

Answer: The mean is (4+8+12)/3=8. The squared differences from the mean are (4−8)²=16,(4−8)²=16, (8−8)²=0 and (12−8)²=16, (12−8)²=16. The sum of squares is 16+0+16=32.

Problem 2: Sum of Squares of the First n Natural Numbers

Calculate the sum of squares of the first 5 natural numbers.

Answer: Use the formula n(n+1)(2n+1)​/6 with n=5: 5(5+1)(2⋅5+1)/6=5⋅6⋅11/6=55

Problem 3: Sum of Squares Error (SSE) in Data Analysis

You conducted an experiment and collected the following observed (y) and predicted (y^​) values:

• Observed (y): 3, 5, 7
• Predicted (y^​): 2, 4, 6

Calculate the SSE.

Answer: Calculate the differences (3−2)²=1, (5−4)²=1, (7−6)²=1, (7−6)²=1. The SSE is 1+1+1=3.

Problem 4: Algebraic Sum of Squares

Find the sum of squares of 3x²−2x+1 and 2x²+3x−4.

Answer: Squaring each term and then adding gives (3x²)²+(−2x)²+1²+(2x²)²+(3x)²+(−4)² which simplifies to 9x⁴+4x²+1+4x⁴+9x²+16, resulting in 13x⁴+13x²+17.

Problem 5: Using Sum of Squares in Regression Analysis

In a simple linear regression analysis, you have calculated the total sum of squares (SST) as 200 and the regression sum of squares (SSR) as 160. Calculate the residual sum of squares (SSE).

Answer: Since SST=SSR+SSE, we find SSE=SST−SSR=200−160=40.

Faqs

Is 35 a Square Number?

No, 35 is not a square number. A square number results from multiplying an integer by itself, and no whole number multiplied by itself gives 35.

What’s the Square of 24?

The square of 24 is $²$ Squaring a number means multiplying it by itself, so 24 multiplied by 24 equals 576.

Is 27 a Square Number?

No, 27 is not a square number. Square numbers are integers that can be expressed as the product of another integer with itself, and there is no integer whose square is 27.

What Are the 14 Square Numbers Up to 200?

The 14 square numbers up to 200 are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, and 196. These represent the squares of the integers from 1 to 14.

Is 30 a Square Number?

No, 30 is not a square number. Square numbers come from squaring integers, and 30 cannot be obtained by squaring any integer.

Is 60 a Square Number?

No, 60 is not a square number. There is no integer that, when multiplied by itself, results in 60, making it not a perfect square.

What Is the 15th Square Number?

The 15th square number is $²$This is because when you multiply 15 by itself, the product is 225.

Why Is 13 Not a Square Number?

13 is not a square number because it cannot be formed by squaring any whole number. Square numbers are the product of an integer multiplied by itself, and no integer squared equals 13.