Square Root Function

The Square Root Function, denoted as 𝑓(𝑥) = √𝑥, is a fundamental concept in algebra that assigns to each non-negative number 𝑥 its non-negative square root. This function intersects various mathematical domains, handling both rational and irrational numbers, as it maps each squared integer or real number back to its original form. In statistical contexts, such as regression analysis, the square and square root function can be employed to transform data, optimizing the application of the least squares method. This transformation is crucial fogr normalizing datasets and reducing skewness, enhancing the accuracy of statistical models and numerical predictions.

Square Root Function?

The square root function is a fundamental mathematical operation that associates each non-negative real number 𝑥 with its non-negative square root. Mathematically, it’s denoted as 𝑓(𝑥) = √𝑥. This function is crucial in various areas of algebra and analysis, as it essentially reverses the operation of squaring a number.

Characteristics of the Square Root Function:

• Domain: The domain of the square root function is all non-negative real numbers [0,∞], because square roots of negative numbers are not defined in the set of real numbers (though they are defined as complex numbers).
• Range: The range is also all non-negative real numbers [0,∞), as the square root of a non-negative number is always non-negative.
• Graph: The graph of 𝑓(𝑥) = √𝑥 is a curve that starts at the origin (0,0) and gradually increases, becoming less steep as 𝑥 increases. This curve is part of a parabola that has been rotated.
• Function Behavior: The square root function increases monotonically, meaning it never decreases as 𝑥 increases. The speed of increase slows down as 𝑥 gets larger, which is characteristic of all root functions.
• Application in Algebra: In algebra, the square root function is vital for solving equations where a variable is squared. It helps in finding the original values after they have been squared.

Square Root Graph

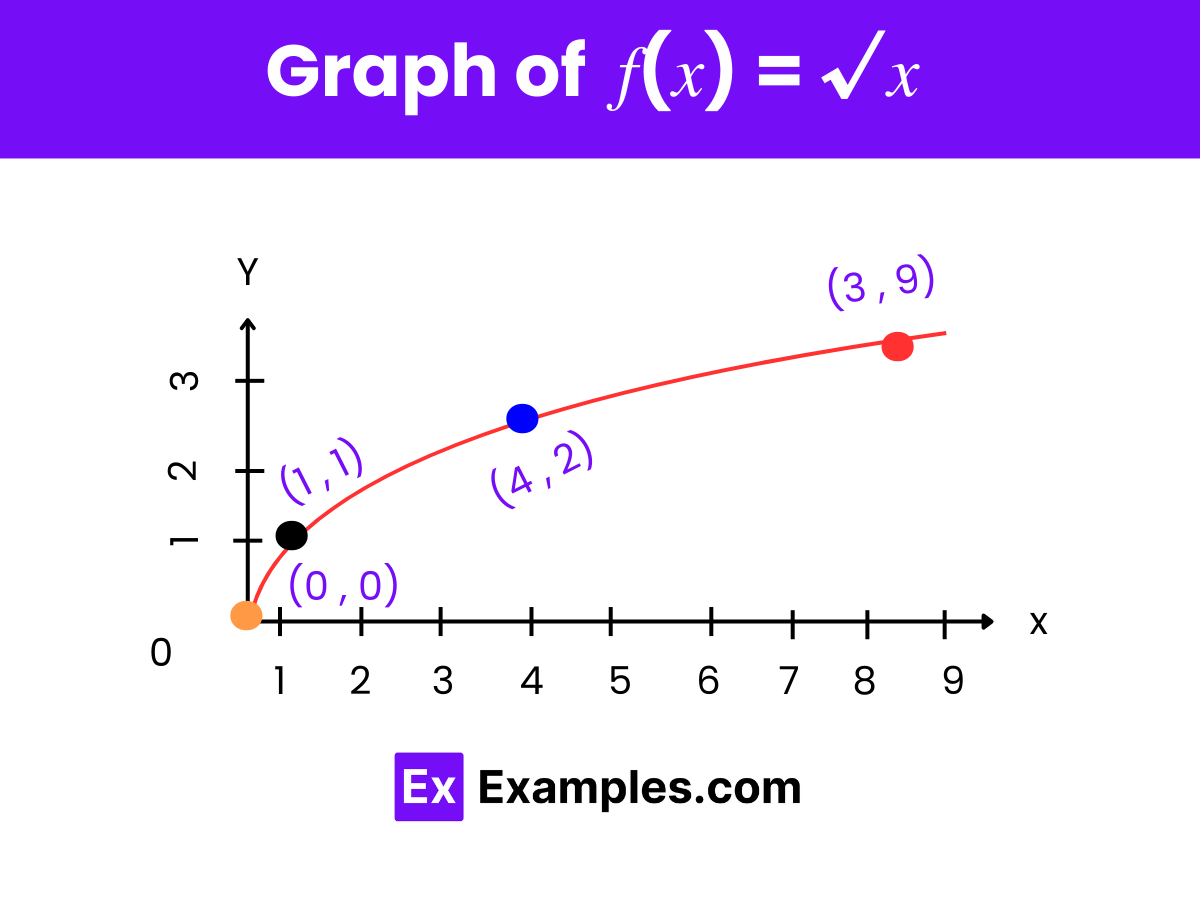
To visualize the square root function 𝑓(𝑥) = √𝑥​, it’s helpful to see its values tabulated alongside the input values. Here’s a table showing selected values for 𝑥 and the corresponding 𝑓(𝑥) values:

x (Input)	𝑓(𝑥) = √𝑥​ (Output)
0	√0 = 0
1	√1 = 1
4	√4 = 2
9	√9 = 3

• Starting Point: The function begins at the origin (0,0).
• Increasing Nature: The function values increase as 𝑥x increases.
• Decreasing Rate of Increase: The increase in 𝑓(𝑥)f(x) becomes slower as 𝑥x gets larger. For instance, the difference between square root values decreases relative to the increase in 𝑥x.

Properties of Square Root Function

Non-Negative Output

• The outputs of the square root function are always non-negative. This arises because the function is defined for non-negative inputs 𝑥≥0, and the square root of a non-negative number cannot be negative.

Subadditive Property

• The square root function exhibits a subadditive property, which states that for any non-negative real numbers 𝑎 and 𝑏,
• √𝑎+𝑏≤√𝑎+√𝑏
• ​This inequality highlights the function’s conservative growth rate when combining inputs.

Slow Growth Rate

• As 𝑥 increases, the rate at which √𝑥​ increases becomes progressively slower. This is mathematically captured by the function’s derivative, 1/2√𝑥​, which decreases as 𝑥 increases, indicating a deceleration in growth.

Reflective Symmetry about y = x

• The square root function is the inverse of the square function restricted to non-negative inputs and outputs. This relationship gives the graph of √𝑥​ reflective symmetry about the line 𝑦 = 𝑥 when considered against its inverse 𝑥² for 𝑥≥0.

Smoothness Except at Origin

• The square root function is smooth (infinitely differentiable) for all 𝑥>0. However, at 𝑥 = 0, the function is not differentiable due to the vertical tangent. This point is technically known as a cusp, where the behavior of the derivative changes abruptly.

Impact on Variance Calculations

• In statistics, the square root transformation is often used to stabilize variance and normalize distributions. This transformation can be particularly effective for data that follow a Poisson or binomial distribution, where variance is proportional to the mean.

Integral Representation

• The function √𝑥​ can be represented as an integral:
• √𝑥 = 2/3𝑥³/²
• This representation is often used in calculus to solve area and volume problems involving shapes and solids generated by revolving the square root curve around an axis.

These properties provide a deeper understanding of the square root function, demonstrating its fundamental role in mathematics and its utility in various theoretical and practical applications.

Square Root Function Examples

Example 1: Calculating the Side Length of a Square Given its Area

Problem: Suppose you have a square plot of land with an area of 625 square meters. What is the length of each side of the square?

Solution:

• The area of a square is given by the formula 𝐴 = 𝑠², where 𝑠s is the side length of the square.
• Given the area 𝐴=625 square meters, to find 𝑠, you take the square root of the area: 𝑠 = 625​
• Calculating the square root, you find: 𝑠 = 25 meters
• Conclusion: Each side of the square plot of land is 25 meters long.

Example 2: Engineering Application in Calculating RMS Voltage

Problem: An alternating current (AC) electrical circuit has a peak voltage of 120 volts. Calculate the root mean square (RMS) voltage, which is the effective voltage of the AC circuit.

Solution:

• The RMS voltage for an AC circuit, where 𝑉ₚₑₐₖ​ is the peak voltage, is given by the formula:
• 𝑉ᵣₘₛ = 𝑉ₚₑₐₖ/√2​​
• Substituting the given peak voltage into the formula: 𝑉ᵣₘₛ = 120​/√2
• Calculating the square root and the division, you find: 𝑉ᵣₘₛ = 84.85 volts
• Conclusion: The RMS voltage of the circuit is approximately 84.85 volts, which represents the effective voltage that would deliver the same power to a resistive load as a direct current (DC) of that voltage.

FAQs

How does the square root function affect statistical data analysis?

In statistics, the square root transformation is often applied to data to stabilize variance and normalize distributions, particularly in data sets skewed by large outliers. This transformation can make patterns more apparent and data analysis techniques more effective.

Can the square root function be graphed, and what does it look like?

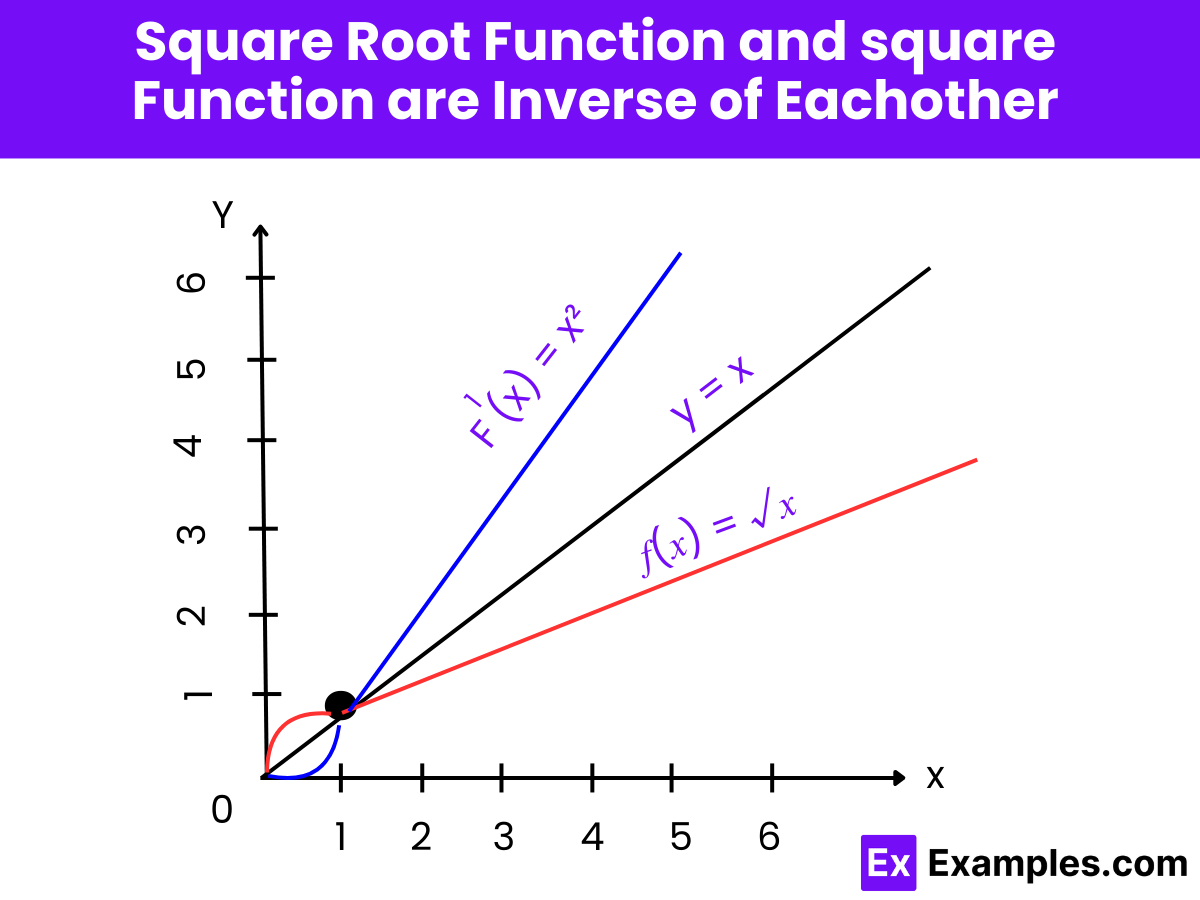
Yes, the graph of the square root function is a curve that starts at the origin (0,0) and gradually increases. It forms half of a parabola that has been rotated 90 degrees counterclockwise. This curve is always increasing but does so at a decreasing rate as 𝑥 increases.

Why can the square root function only handle non-negative numbers?

The standard square root function is defined only for non-negative numbers because the square root of a negative number is not a real number; it is an imaginary number. This limitation ensures that the function remains applicable and meaningful in real-world scenarios without the need for complex number calculations.