square & square root of 1000
square & square root of 1000
Square of 1000
The square numbers of 1000, or 1000 squared, equals 1,000,000. This result signifies the area of a square with sides measuring 1000 units. It holds significance in math and practical applications for its magnitude and precision.
Square Root of 1000
or
√1000 = 31.622
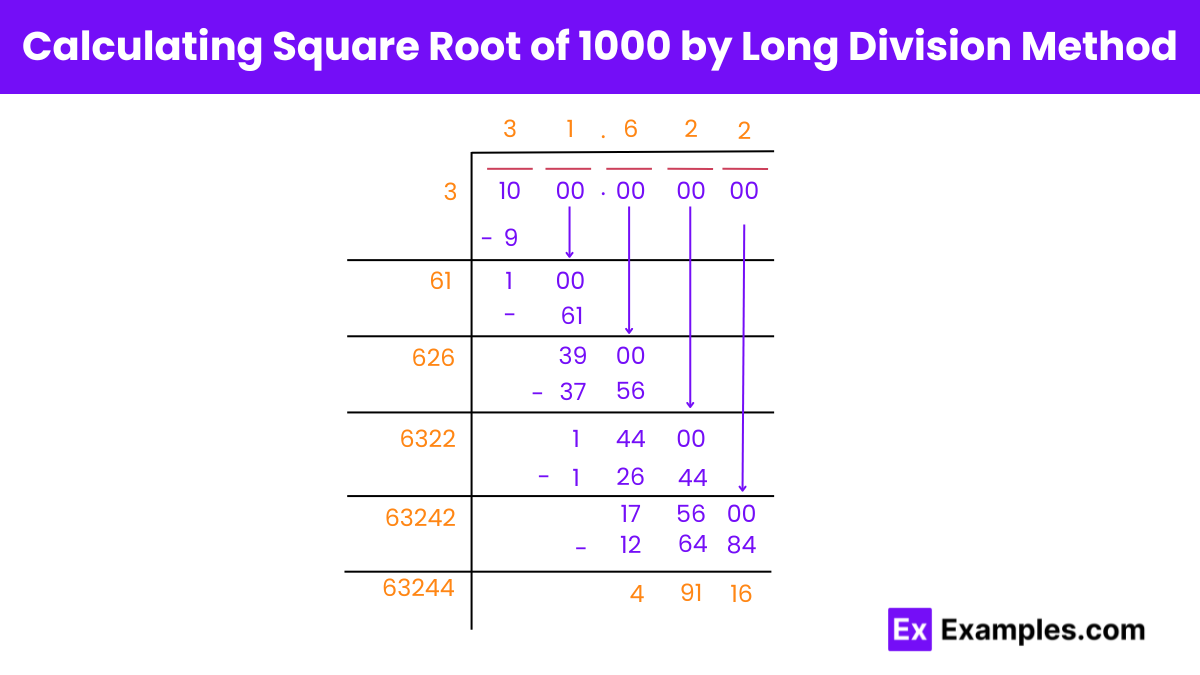
The square root of 1000 is expressed as √1000. It equals approximately 31.62 because 31.62 multiplied by itself (31.62 × 31.62) equals 1000. Mathematically, finding the square root of a number involves determining the non-negative value x such that f(x) = 1000 in the function f(x) = x².
Square Root of 1000 : 31.622
Exponential Form: 1000^1/2 or 1000^0.5
Radical Form: √1000
Is the Square Root of 1000 Rational or Irrational?
Irrational numbers cannot be expressed as fractions of integers. The square root of 1000, approximately 31.62, cannot be simplified to a fraction. It is a non-repeating, non-terminating decimal, making it irrational and not expressible as a simple fraction.
rational numbers are those that can be expressed as the quotient of two integers, where the denominator is not zero.
Examples : 1/2, -3, and 5.
Irrational numbers can’t be written as fractions of integers. Their decimal forms go on forever without repeating. They show up in geometry and algebra, like square roots of non-perfect squares or π.
Examples : √2 ,√3 , √5 , π (pi)
Methods to Find Value of Root 1000
- Estimation: Using approximation techniques like the Babylonian method.
- Calculator: Utilizing a calculator or a computer software to calculate the square root directly.
- Table lookup: Referring to square root tables or online resources for the value.
- Algebraic manipulation: Employing algebraic techniques to simplify or approximate the value.
Square Root of 1000 by Long Division Method
- Start with Decimal Form: Write 1000 as 1000.000000.
- Pair the Number: Pair digits from right to left with a bar on top.
- Find Initial Quotient and Remainder: Divide 10 by a number, yielding a product less than or equal to 10. The quotient is 3 with a remainder of 1.
- Double the Quotient: Obtain 6 and assume 60 as the new divisor. Bring down 00 for division.
- Find Next Quotient and Remainder: Find a number such that (60 + number) × number ≤ 100. It’s 61, resulting in a quotient of 31 and a remainder of 39.
- Repeat the Process: Continue this process, doubling the quotient each time and bringing down the appropriate digits, until reaching the desired level of precision.
- Obtain Approximation: The approximate square root of 1000 is 31.622.
Is 1000 Perfect Square root or Not
No, because it cannot be expressed as the square of an integer. Its square root is approximately 31.622776, which is not a whole number. Therefore, 1000 is not a perfect square root.
FAQ’S
How do you find the square root of 1000?
The square root of 1000 can be found using methods like estimation, calculator, or algebraic manipulation.
Why is the square root of 1000 important?
The square root of 1000 is important in mathematics and various fields for calculations involving area, geometry, and algebraic equations.
Why is the square root of 1000 not a whole number?
The square root of 1000 is not a whole number because 1000 is not a perfect square.
Can the square root of 1000 be simplified further?
No, the square root of 1000 cannot be simplified further as it is an irrational number.
What is the significance of 1000 in mathematics?
1000 is a milestone number and is used as a base in various numerical systems and calculations.
Share :
