Square & Square Root of 194
Square & Square Root of 194
Square of 194
The square number of 194 is 37,636. This number represents the result when 194 is multiplied by itself. It’s a large number, indicating the area of a square with sides of length 194 units. It’s divisible by several smaller squares, making it significant in mathematical calculations and geometric contexts.
Square Root of 194
The square root of 194 is approximately 13.93. It’s the value that, when multiplied by itself, equals 194. This is a fundamental concept in mathematics and geometry. 13.93 is an irrational number and a factor in the context of 194.
Square Root of 194: 13.92
Exponential Form: 194^½ or 194^0.5
Radical Form: √194
Is the Square Root of 194 Rational or Irrational?
Rational numbers are numbers that can be expressed as a fraction of two integers, where the denominator is not zero. They include integers, finite decimals, and repeating decimals.
Irrational numbers are numbers that cannot be expressed as a fraction of two integers. They have non-repeating, non-terminating decimal expansions.
Methods to Find Value of Root 194
1. Long Division Method:
- This traditional method involves a step-by-step process of guessing, dividing, and averaging to find a more precise value of the square root. It’s time-consuming but yields accurate results.
2. Prime Factorization:
- Although this method works well for perfect squares, it is not effective for 194, which is not a perfect square. Thus, this method is not suitable for finding the square root of 194.
3. Using a Calculator:
- The quickest and easiest method is to use a scientific calculator. Enter 194 and press the square root (√) button to get an approximate value, which is about 13.93.
4. Estimation Method:
- Find the two perfect squares closest to 194 (i.e., 169 and 196, whose square roots are 13 and 14, respectively). Estimate that the square root of 194 is between 13 and 14, and refine further if needed.
5. Newton’s Method (Heron’s Method):
- Start with an initial guess (e.g., 14) and iterate using the formula xₙ₊₁ = 1/2 (xₙ+194/xₙ). Repeat until the value converges to a stable value close to 13.93.
Square Root of 194 by Long Division Method
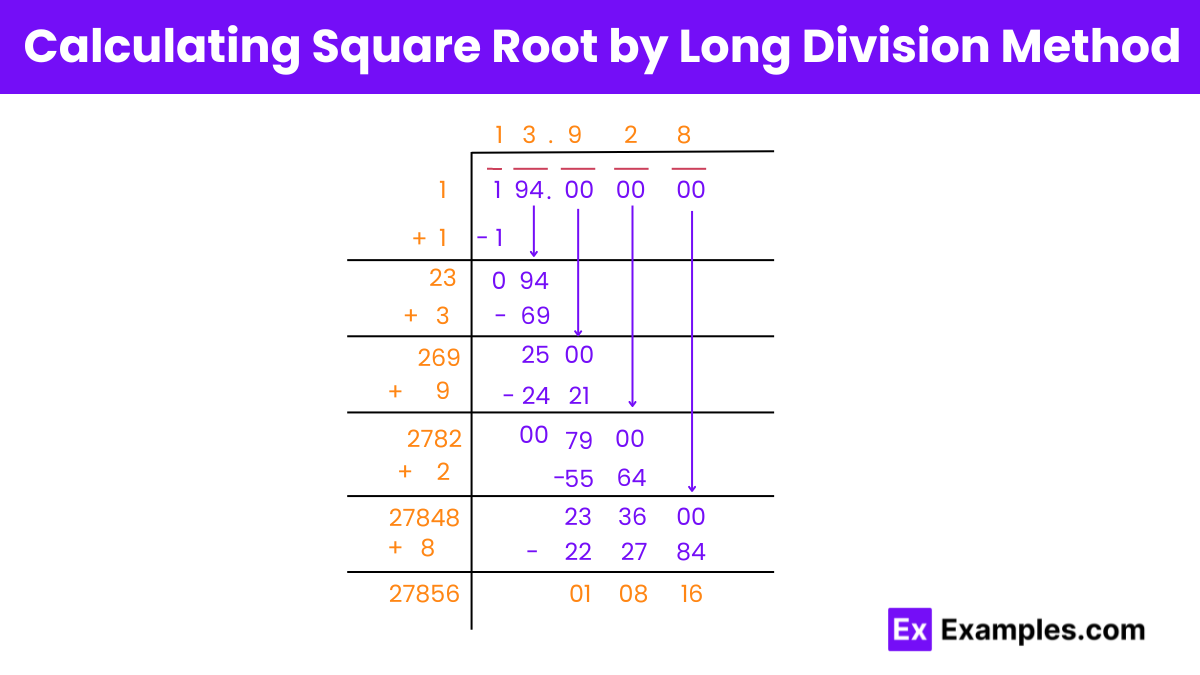
Start pairing the digits by adding a bar on top of them from the unit’s place in pairs of two. We have two pairs: (1 & 94).
1. First Pair:
- Find a number ( a ) such that ( a × a ≤ 1 ). Here, ( a ) is 1 because ( 1× 1 = 1 ).
- The quotient is 1. Add the divisor ( a ) with itself to get the new divisor (2). Bring down the next pair (94), making the dividend 094.
2. Second Pair:
- Find a number ( y ) such that ( 2y ×≤ 94 ). The number ( y ) is 3 because ( 23 × 3 = 69 ≤ 94 ).
3. Add Decimals:
- Place a decimal point in the dividend and quotient simultaneously. Add three pairs of zeros to the dividend part after the decimal.
4. Continue Long Division:
- Repeat the above steps for the three pairs of zeros.
Using this method, the square root of 194 is approximately 13.928.
Is 194 Perfect Square root or Not
A perfect square is a number that can be expressed as the square of an integer. Since the square root of 194 is not an integer, 194 is not a perfect square.
FAQ’s
What’s the nearest perfect square to 194?
169 (13^2) and 196 (14^2).
What’s the significance of 194 in mathematics?
It’s a non-perfect square, useful for practicing square roots.
Is 194 a prime number?
No, it’s divisible by 2
Can 194 be written as a product of primes?
Yes, as 2 * 97.
How many factors does 194 have?
Four: 1, 2, 97, and 194.
What’s the digital root of 194?
1 (1+9+4 = 14, 1+4 = 5, 5+0 = 5).
Share :
