Square & Square Root of 245

Within the realm of algebraic mathematics, squares and square roots are pivotal concepts. Squaring a number, like 245, involves multiplying it by itself, yielding 60025. This operation is foundational, crucial in exploring rational and irrational numbers. Understanding these basics enriches comprehension of mathematical relationships and patterns. Squares reveal inherent properties of numbers, while square roots unravel complex numerical mysteries. These concepts illuminate mathematical landscapes, guiding explorations into fractional territories. Mastery of squares and square roots empowers mathematicians to navigate diverse mathematical terrains, uncovering the elegance and complexity woven within algebraic frameworks.

Square of 245

245² (245 × 245) = 60025

The square number 245 equals 60025, derived by multiplying 245 by itself, a fundamental operation in algebraic mathematics, revealing inherent properties of numbers.

Square Root of 245

√245 ≈ 15.6524758

or

√245 ≈ 15.652 Upto 3 decimals

The square root of 245 is approximately 15.652. This fundamental operation in mathematics uncovers the value that, when multiplied by itself, equals 245.

Square Root of 245:Approximately 15.652

Exponential Form: 245^½ or 245^0.5

Radical Form: √245

Is the Square Root of 245 Rational or Irrational?

No, the square root of 245 is an irrational number.

Rational Numbers: Rational numbers are those that can be expressed as the quotient of two integers, where the denominator is not zero. In other words, they can be written as fractions of the form a/b where (a) and (b) are integers and (b ≠ 0). Rational numbers include integers and fractions. Examples of rational numbers include 1/2, -3, and 5/7.

Irrational Numbers: Irrational numbers cannot be expressed as fractions of integers. Their decimal representations are non-repeating and non-terminating. These numbers cannot be represented as finite or repeating decimals. Examples of irrational numbers include the square roots of non-perfect squares like √2, √3, and √5, as well as transcendental numbers like π.

In essence, rational numbers can be expressed as fractions with finite or repeating decimals, whereas irrational numbers cannot be represented in this way, having non-repeating, non-terminating decimal expansions.

Methods to Find the Value of Root 245

Prime Factorization Method: Break down 245 into its prime factors, which are 5 × 7 × 7. The square root of 245 is approximately 15.652, but since it doesn’t result in a perfect square, it remains an approximation.

Long Division Method: Use the long division algorithm to find the square root of 245 by approximation. Start with a guess (e.g., 15) and refine iteratively.

Using a Calculator: Most calculators have a square root function. Simply input 245 and find the square root directly.

Estimation: Since 245 is close to the perfect square of 256 (16 × 16), you can estimate that its square root is slightly less than 16.

Square Root of 245 by Long Division Method

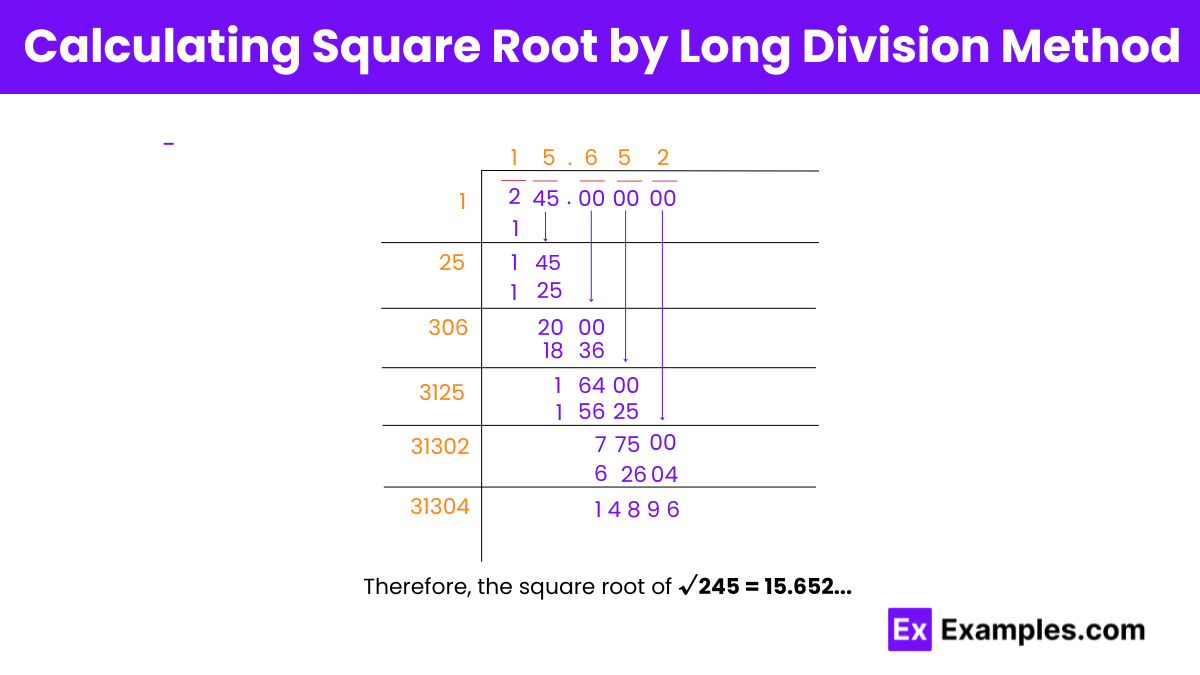
Step 1: Pair the digits of 245 starting with the digit at one’s place. Place a horizontal bar to indicate pairing: 2|45.

Step 2: Find a number which, when multiplied by itself, gives a product less than or equal to 2. As we know, 1 × 1 = 1 < 2. So, 1 is the quotient and the remainder is 1.

Step 3: Bring down 45 to the right of 1, making the new dividend 145. Double the quotient obtained in Step 2, which gives us 2. Hence, 2 is the starting digit of the new divisor.

Step 4: Determine a digit to place at the unit’s place of the new divisor. Here, 5 works because 25 × 5 = 125 ≤ 145. Subtracting 125 from 145 gives us 20. The quotient now is 15.

Step 5: Bring down the next pair of zeros, making the new dividend 2000. Double the current quotient (15), resulting in 30, which becomes the starting digit of the new divisor.

Step 6: Determine the next digit to place at the unit’s place of the divisor. Here, 6 works because 306 × 6 = 1836 ≤ 2000. Subtracting 1836 from 2000 gives us 164. The quotient now is 156.

Step 7: Bring down the next pair of zeros, making the new dividend 16400. Double the current quotient (156), resulting in 312, which becomes the starting digit of the new divisor.

Step 8: Determine the next digit to place at the unit’s place of the divisor. Here, 5 works because 3125 × 5 = 15625 ≤ 16400. Subtracting 15625 from 16400 gives us 775. The quotient now is 1565.

Step 9: Bring down the next pair of zeros, making the new dividend 77500. Double the current quotient (1565), resulting in 3130, which becomes the starting digit of the new divisor.

Step 10: Determine the next digit to place at the unit’s place of the divisor. Here, 2 works because 31302 × 2 = 62604 ≤ 77500. Subtracting 62604 from 77500 gives us 14896. The quotient now is 15652.

Step 11: Bring down the next pair of zeros, making the new dividend 1489600. Double the current quotient (15652), resulting in 31304, which becomes the starting digit of the new divisor.

Step 12: Continue this process until you reach the desired level of precision. In this context, we would typically stop after a few decimal places.

The approximate value of the square root of 245, calculated to several decimal places, is around 15.652.

Is 245 a Perfect Square?

No, the number 245 is not a perfect square.

245 is not a perfect square because it cannot be expressed as the square of an integer. The square root of 245 is approximately 15.652, which is not a whole number, indicating that 245 is not a perfect square.