Square & Square Root of 33

Within algebraic studies, the significance of squares and square roots is foundational. Squaring, exemplified by multiplying a number like 33 by itself to yield 1089, is fundamental. This operation underpins investigations into properties of rational and irrational numbers. Understanding these concepts enriches comprehension of mathematical relationships and patterns, crucial in algebraic studies and beyond. In the realm of mathematics, squares and square roots are pivotal. Squaring, demonstrated by multiplying 33 by itself to produce 1089, serves as a cornerstone. This process facilitates exploration into the properties of both rational and irrational numbers, deepening comprehension of mathematical relationships and patterns within algebraic studies and beyond.

Square of 33

33² (33 × 33) = 1089

A square number, such as 33, results from multiplying an integer by itself. The square of 33 equals 1089. This fundamental operation illuminates algebraic principles, showcasing the inherent properties of rational and irrational numbers, enriching understanding of mathematical relationships and patterns within the realm of algebraic studies.

Square Root of 33

√33 = 5.744

Or

√33 = 5.744 Upto 3 decimals

The square root of 33, a non-square number, is an irrational number approximately equal to 5.744. Understanding square roots involves finding the number that, when multiplied by itself, equals 33. Mastery of square roots unveils fundamental mathematical concepts, essential for exploring algebraic relationships and patterns.

Square Root of 33: 5.744

Exponential Form: 33^½ or 33^0.5

Radical Form: √33

Is the Square Root of 33 Rational or Irrational?

The square root of 33 is an irrational number

The square root of 33 is irrational. It cannot be expressed as a fraction of two integers, and its decimal representation continues infinitely without repeating. Thus, it falls under the category of irrational numbers.

Rational Numbers: Rational numbers can be expressed as fractions of two integers, like 3/4 or -5/2.

Irrational Numbers: Irrational numbers cannot be written as fractions of integers. Their decimal expansions neither terminate nor repeat. For instance, the square root of 2 (√2) ≈ 1.41421356… is irrational.

Methods to Find Value of Root 33

Several methods can be used to find the square root of 33:

Estimation Method: Make an initial guess, then refine it iteratively using approximation techniques like the Newton-Raphson method.

Prime Factorization Method: Express 33 as a product of prime factors (3 × 11), then find the square root of each prime factor.

Long Division Method: Apply long division to iteratively find the digits of the square root.

Calculator: Utilize a calculator with a square root function to directly compute the square root of 33.

Square Root of 33 by Long Division Method

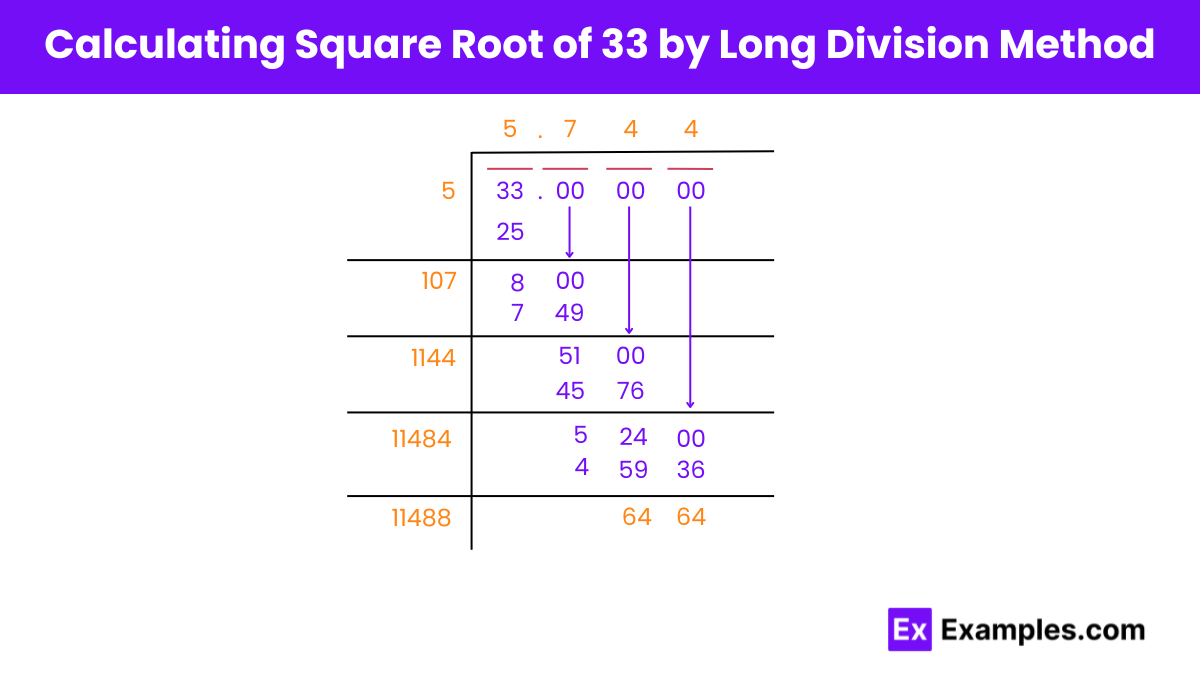
Finding the Square Root of 33 Using the Long Division Method

Step 1: Setup
Write 33 as 33.000000 (to facilitate the long division process).

Step 2: Initial Division
Divide 33 by a number such that the number multiplied by itself gives 33 or a number less than that. Since 5 × 5 = 25, use 5 as the initial divisor. Subtracting 25 from 33 yields 8. Bring down a pair of zeros, making the new dividend 800.

Step 3: Iterative Division

• Quotient Calculation: Quotient is 5. Double the quotient to get 10, which is placed at the new divisor’s position.
• Finding Next Digit: Find a number in place of x such that 10x × x gives a product less than or equal to 800. Determining 107× 7 = 749, subtract it from 800 to yield a remainder of 51.
• Continued Iteration: Bring down the next pair of zeros, double the quotient to get 114, and place 114x at the new divisor’s position. Find a number in place of x such that 114x × x gives a product less than or equal to the current remainder.

Step 4: Final Result
Repeat the process until the desired level of accuracy is achieved. Thus, the square root of 33 is approximately 5.744, rounded to the nearest thousandth.

33 is Perfect Square root or Not

No, 33 is not a perfect square number

No, 33 is not a perfect square. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. Since there are no integers where the product of the integer with itself equals 33, it is not a perfect square.

FAQs

What are some properties of the square and square root of 33?

The square of 33 is a positive integer, while the square root of 33 is a positive irrational number.

How do I verify if my calculation of the square root of 33 is correct?

You can verify your calculation by squaring the square root value obtained. If the result is 33, then your calculation is correct.

What are some real-life applications of understanding squares and square roots?

Understanding squares and square roots is essential in various fields such as engineering, physics, computer science, and finance for tasks like calculating areas, distances, and determining quantities.

Is there a pattern in the digits of the square root of 33?

The decimal representation of the square root of 33 is non-repeating and non-terminating, indicating no discernible pattern in its digits.

How does knowing the square and square root of 33 contribute to my understanding of algebraic concepts?

Understanding squares and square roots serves as a foundational step in algebra, helping to comprehend concepts like equations, inequalities, and polynomial functions.