Square & Square Root of 57

Within the domain of mathematics, particularly in algebraic studies, squares and square roots are fundamental. Squaring a number, such as 57 resulting in 3249, is pivotal. This operation unveils properties of rational (expressible as a fraction) and irrational numbers (defying neat fraction expression). Understanding these concepts enriches comprehension of mathematical patterns and relationships, crucial for navigating complexities in algebraic explorations. Mastery of these foundational principles fosters a deeper understanding of mathematical structures, enabling one to discern intricate connections within numerical systems. Thus, the study of squares and square roots transcends mere arithmetic, evolving into a profound exploration of algebraic concepts, essential for comprehending the underlying principles governing mathematical phenomena.

Square of 57

57² (57 × 57) = 3249

The square number of 57 is 3249. In mathematics, a square number arises when an integer is multiplied by itself. Understanding the properties and patterns of square numbers, like 57 squared, enriches comprehension of algebraic concepts, fostering a deeper insight into mathematical relationships and structures.

Square Root of 57

√57 = 7.54983443527

Or

√57 = 7.549 Upto 3 Decimals

The square root of 57 is approximately 7.55. In mathematics, the square root signifies the number that, when multiplied by itself, equals 57. Exploring the square of 57 reveals fundamental principles, enriching comprehension of mathematical relationships and patterns embedded within numerical systems.

Square Root of 57: 7.54983443527

Exponential Form: 57^½ or 57^0.5

Radical Form: √57

Is the Square Root of 57 Rational or Irrational?

The square root of 57 is an irrational number

The square root of 57 is irrational. It cannot be expressed as a simple fraction of two integers. This classification distinguishes it from rational numbers, which can be represented in such a form, highlighting the complexity within mathematical systems.

Rational number : A rational number is one that can be written as a fraction of two integers.

For example, 3/4 or -5/2 are rational.

Irrational number : An irrational number cannot be expressed as a fraction of two integers, and its decimal expansion neither ends nor repeats.

For instance, √2 ≈ 1.41421356… is irrational.

Methods to Find Value of Root 57

To find the square root of 57, you can use various methods:

Prime Factorization: Break down 57 into its prime factors to simplify calculation.

Estimation: Use nearby perfect squares to approximate the root.

Newton’s Method: Iteratively refine guesses to converge on the precise value.

Calculator or Software: Utilize technology for accurate and rapid computation.

Long Division Method: Employ a step-by-step division process to manually extract the root.

Square Root of 57 by Long Division Method

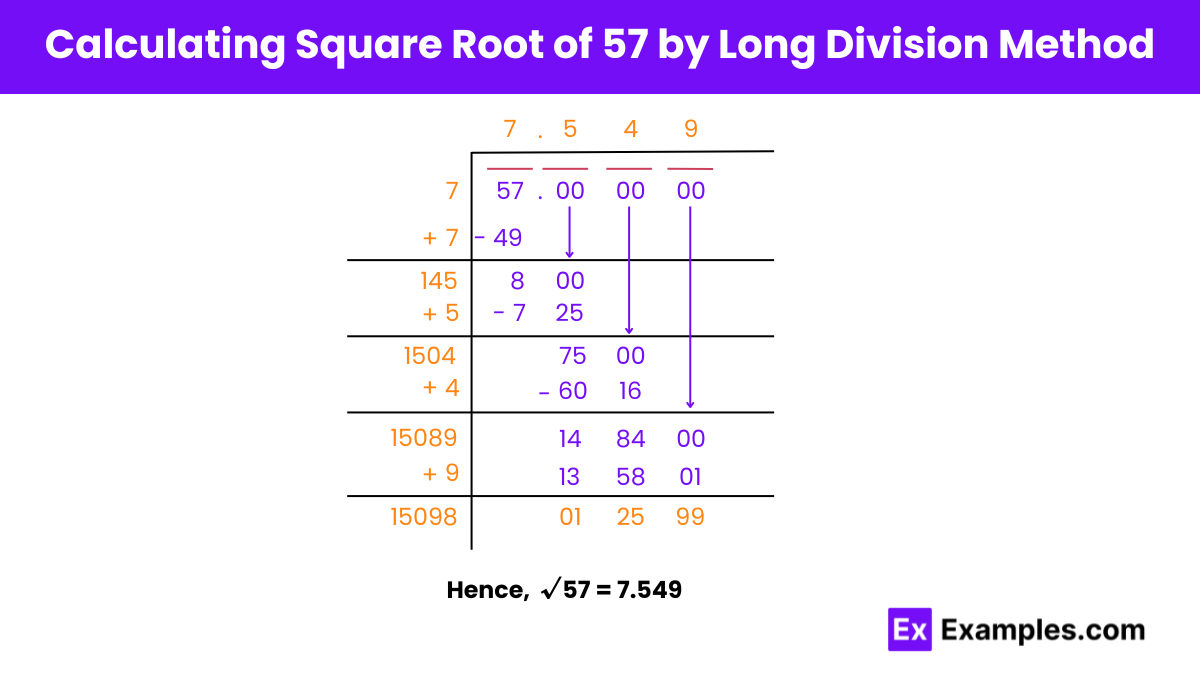
Step 1: Grouping Digits
Group digits from the unit’s place in pairs of two, yielding one pair (57).

Step 2: Finding Initial Guess
Find a number (t) where t × t ≤ 57. Thus, t = 7 (7 × 7 = 49).

Step 3: First Division
Divide 57 by 7, resulting in a quotient of 7 and a remainder of 8. Add the divisor (7) with itself to get the new divisor (14).

Step 4: Decimal Placement
Introduce a decimal in the dividend and quotient. Add three pairs of zero to the dividend (57. 00 00 00).

Step 5: Continuing Division
Bring down the pair of zero, yielding a new dividend of 800. Find a number (m) where 14m × m ≤ 800. Thus, m = 5 (145 × 5 = 725 ≤ 800).

Step 6: Repeat for Remaining Digits
Repeat the process for all pairs of zero.

Step 7: Conclusion
The square root of 57, calculated by the long division method, is approximately 7.549.

57 is Perfect Square root or Not

No, 57 is not a perfect square number

57 is not a perfect square because it cannot be expressed as the square of an integer. Its square root is approximately 7.549, which is not an integer, indicating that 57 is not a perfect square.

FAQs

Can 57 be simplified in terms of its square root?

No, as 57 is not a perfect square, its square root cannot be simplified further.

What is the significance of the square root of 57 in geometry?

The square root of 57 is used in geometric calculations, such as finding the diagonal of a rectangle with side lengths of 57 units.

How does the square root of 57 relate to Pythagorean triples?

The square root of 57 is involved in Pythagorean triples, such as (19, 20, 29), where 19² + 20² = 29².

Is there a pattern in the decimal expansion of the square root of 57?

Yes, the decimal expansion of the square root of 57 continues indefinitely without repeating, showcasing its irrationality.

How does the square root of 57 compare to other square roots?

Compared to perfect squares, such as 49 and 64, the square root of 57 falls between their respective square roots, highlighting its position within the number line.