Square & Square Root of 600
Square & Square Root of 600
Within the domain of algebraic mathematics, squares and square roots hold significant importance. Squaring a number, such as 600, entails multiplying it by itself, yielding 360000. This foundational operation is vital for exploring rational and irrational numbers. A grasp of these fundamentals enriches understanding of mathematical relationships and patterns. Squares illuminate inherent number properties, while square roots unravel intricate numerical mysteries. These concepts serve as beacons, guiding mathematical explorations into fractional territories. Proficiency in squares and square roots equips mathematicians to navigate varied mathematical landscapes, unveiling the elegance and complexity inherent within algebraic frameworks.
Square of 600
The square of 600 equals 360,000, obtained by multiplying 600 by itself, a fundamental operation in algebraic mathematics, uncovering inherent number properties.
Square Root of 600
Or
√600 ≈ 24.494 Upto 3 decimals
The square root of 600 is approximately 24.495. This fundamental mathematical operation reveals the value that, when multiplied by itself, equals 600.
Exponential Form: 600^½ or 600^0.5
Radical Form: √600
Is the Square Root of 600 Rational or Irrational?
Rational numbers are expressible as the quotient of two integers. Irrational numbers, however, cannot be represented as fractions of integers. Examples of irrational numbers include the square roots of non-perfect squares.
Methods to Find the Value of the Root 600
- Prime Factorization Method: Break down 600 into its prime factors. However, since 600 is not a perfect square, its prime factorization results in a mixture of prime factors.
- Long Division Method: Utilize the long division algorithm to approximate the square root of 600 iteratively.
- Using a Calculator: Most calculators are equipped with a square root function, enabling direct calculation of the square root of 600.
- Estimation: As 600 falls between the perfect squares of 529 (23 × 23) and 625 (25 × 25), an estimate can be made that its square root is likely between 24 and 25, closer to 24.
Square Root of 600 by Long Division Method
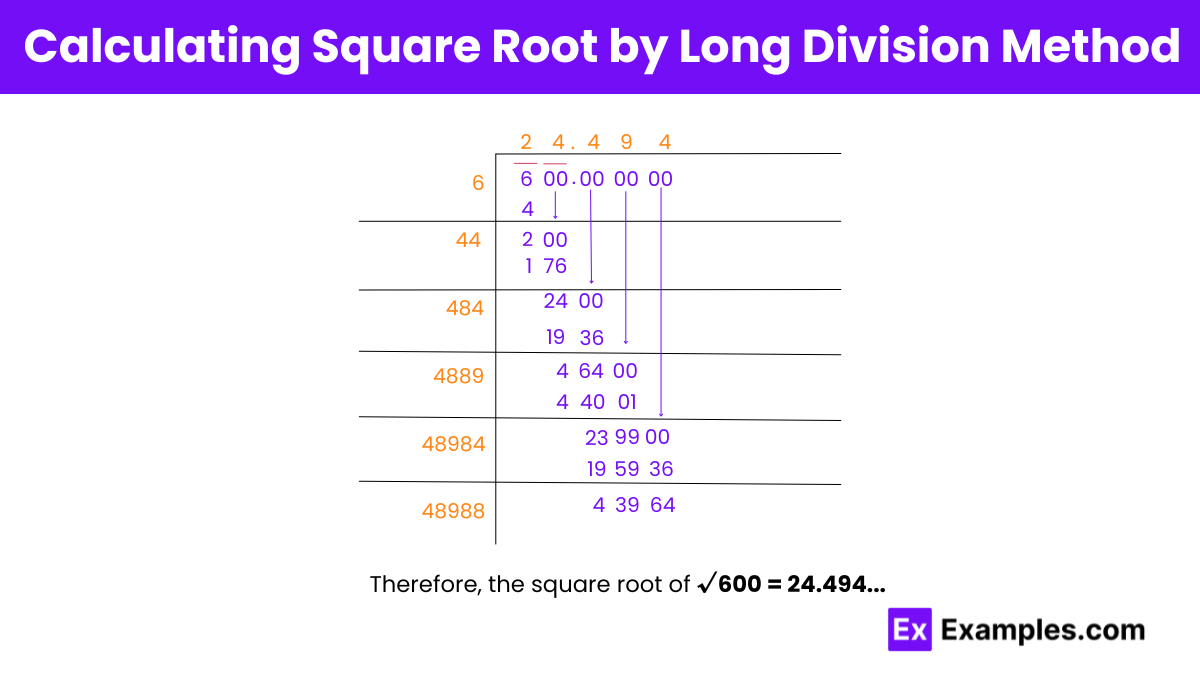
Step 1: Express 600 as 6 00.00 00. We take the number in pairs from the right. Take 6 as the dividend.
Step 2: Now find a quotient which is the same as the divisor. Multiply quotient and the divisor. (2 × 2 = 4) and subtract the result from 6 and get the remainder as 2.
Step 3: Bring down the pair of zeros. 200 is our new dividend.
Step 4: Now double the quotient obtained in step 2. Here it is (2 × 2 = 4). 40 becomes the new divisor.
Step 5: We need to choose a number such that (number + 40)× (number) gives a number ≤ 200. (40 + 4) × 4 = 176
Step 6: Subtract this from 200. Get the remainder as 24. Get the next pair of zeros down. 2400 is the new dividend.
Step 7: Now the quotient is 24. Double it. Here it is 48. 480 becomes the new divisor. Now find a (number + 480) × number) that gives ≤ 2400. We find that (484 × 4 = 1936). Get the remainder as 464.
Step 8: Repeat the process until we get the square root of 600 approximated to two decimal places. Thus, ( √600 ≈ 24.494 ).
Is 600 a Perfect Square or Not?
A perfect square cannot be expressed as the square of an integer. Therefore, the square root of 600 is an irrational number.
What is the square root of 600 to the nearest whole number?
The square root of 600 to the nearest whole number is 24, obtained by finding the integer value that, when squared, equals or is closest to 600.
How does prime factorization relate to the square root of 600?
Prime factorization breaks down 600 into its prime factors (2, 2, 2, 3, 5, 5), aiding in determining the exact square root or identifying if it’s irrational.
What are the properties of the square root of 600?
The square root of 600 is approximately 24.495. It’s irrational, non-integer, positive, and can be represented as a decimal or radical form.
Share :
