Square & Square Root of 7
Square of 7
The square of 7, denoted as 7², is the result of multiplying the number 7 by itself. In mathematical terms, squaring a number means raising it to the power of 2. So, when we square 7, we get 49 as the result. In simple terms, the square of 7 is the area of a square with side length 7 units, making it a fundamental concept in arithmetic and geometry
Square Root of 7
or
√7=2.645 up to three places of decimal
The square root of 7, denoted as √7, is a value such that when multiplied by itself, yields 7. In simpler terms, it’s the number whose square equals 7. This value is irrational, meaning it can’t be expressed as a simple fraction and its decimal goes on indefinitely without repetition.
Understanding the square root of 7 is vital in geometry, algebra, and calculus. It helps in determining side lengths of squares, solving quadratic equations, and various calculus calculations.
Despite its simplicity, the square root of 7 embodies the complexity and beauty of mathematics, challenging conventional notions of numbers while offering insights into their intricacies.
Exponential Form:7^½ or 7^0.5
Radical Form:√7
Is the Square Root of 7 Rational or Irrational?
The square root of 7 is an irrational number.
To understand why, let’s delve into the definitions of rational and irrational numbers.
- Rational numbers are those that can be expressed as a fraction of two integers, where the denominator is not zero. In other words, they can be written in the form a/b, where a and b are integers and b is not equal to zero.
Examples of rational numbers include 1/2, -3, and 5.
An irrational numbers cannot be expressed as a simple fraction of two integers. Their decimal representations are non-repeating and non-terminating.
Examples of irrational numbers include √2, π (pi), and √3.
When considering the square root of 7, it becomes apparent that it falls into the realm of irrationality. Unlike rational numbers, it cannot be expressed as a simple fraction. Attempting to represent it as a decimal reveals its infinitely expanding and non-repeating nature. The decimal representation of √7 continues indefinitely without settling into a predictable pattern. The irrationality of the square root of 7 is not just a mathematical curiosity but a fundamental property with significant implications. It underscores the inherent complexity and richness of the number system. While rational numbers offer straightforward representations, irrational numbers like the square root of 7 introduce layers of intricacy and depth to mathematical discourse. In summary, the square root of 7 stands as an exemplar of irrationality in the number system. Its inability to be expressed as a simple fraction and its infinitely expanding decimal representation affirm its classification as an irrational number, highlighting the diversity and complexity inherent in mathematical concepts.
Methods to Find Value of Root 7
To find the value of √7 in an easy and understandable way, try the following simple estimation method:
- Guess and Check Method:
- Start with an initial guess, such as 2 or 3.
- Square the guess and compare it to 7.
- Adjust your guess based on whether the squared result is too high or too low.
- Repeat the process until you get close to the actual square root of 7.
- Estimation Method:
- Understand that the square root of 7 falls between 2 and 3.
- Use knowledge of perfect squares (2^2 = 4, 3^2 = 9) to estimate where the square root of 7 might lie within this range.
- Make an educated guess and refine it through trial and error until you converge on the square root of 7.
- Pattern Recognition Method:
- Recognize that the square root of 7 is closer to the square root of 4 (which is 2) than to the square root of 9 (which is 3).
- Use this pattern to guide your estimation, starting with a guess closer to 2 than to 3.
- Continuously refine your estimate until you get closer to the square root of 7.
- Visual Representation Method:
- Draw a number line between the square roots of consecutive perfect squares (2 and 3).
- Estimate where the square root of 7 might fall on this number line based on its position between the known perfect squares.
- Use the visual aid of the number line to refine your estimation until you reach the value of the square root of 7.
Square Root of 7 by Long Division Method
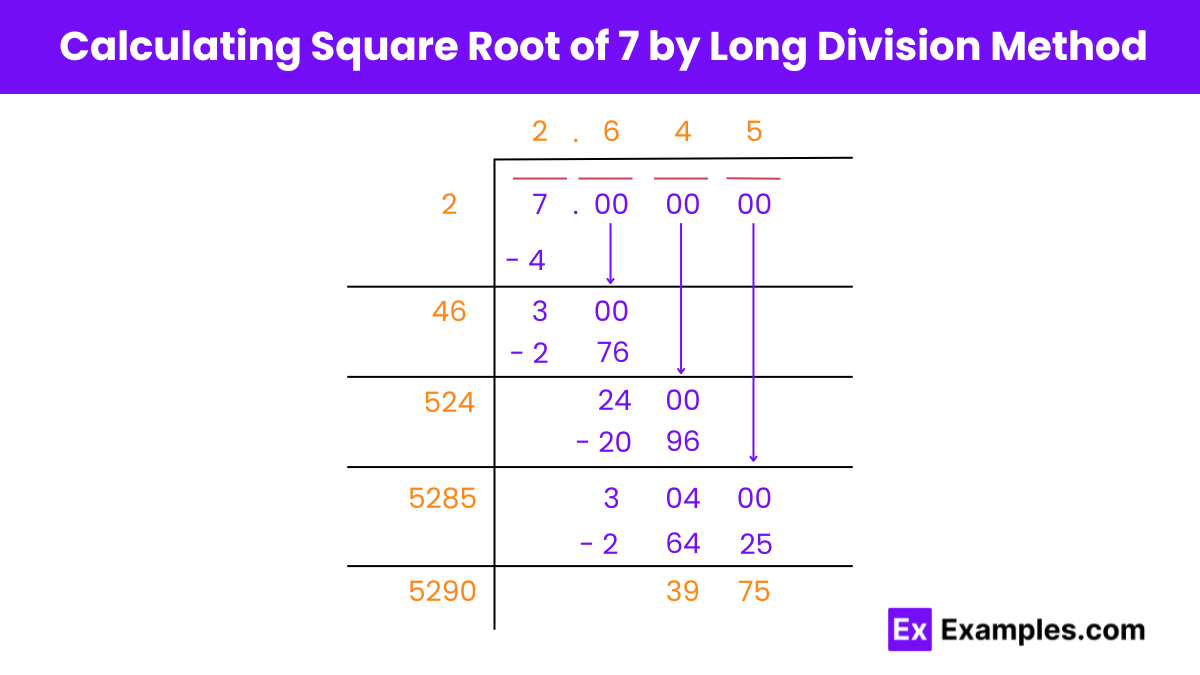
The long division method is a manual technique used to find the square root of a number. Here’s a detailed explanation of how to find the square root of 7 using this methods:
- Setup:Write down the number 7 and group the digits into pairs, starting from the decimal point if there is one. Since 7 is a single-digit number, we start with it.
- Divide and Guess:Start with the largest digit that, when squared, is less than or equal to 7. In this case, it’s 2 (2^2 = 4). Write 2 as the first digit of the square root.
- Divide and Multiply:Divide 7 by the number written above (2) and multiply the result by the same number (2). This gives us 4.
- Subtract and Bring Down:Subtract 4 from 7, leaving us with 3. Bring down the next pair of digits if there were any (which there aren’t in this case, as 7 is a single-digit number).
- Repeat:Repeat steps 2 to 4 until you have enough decimal places or reach the desired level of accuracy. Since 7 is a small number, we can stop here.
- Final Result:The square root of 7, calculated using the long division method, is approximately 2.645751311.
Using the long division method, we can approximate the square root of 7 manually, step by step, without the need for a calculator or advanced mathematical techniques.
7 is Perfect Square root or Not
7 Is Not a Perfect Square Root
A perfect square root is a number that can be expressed as the product of an integer multiplied by itself. For instance, 4 (2 × 2) and 9 (3 × 3) are perfect square roots.
However, when we examine 7, we find that it cannot be expressed as the product of two identical integers. There are no integers x such that x × x equals 7.
Therefore, 7 is not a perfect square root. It doesn’t have an integer square root. While it does have a square root (√7), it’s an irrational number and not the result of multiplying any whole number by itself.
FAQ’s
Is √ 7 a real number?
Yes, the square root of 7, denoted as √7, is a real number. A real number is any number that can be found on the number line, including both rational and irrational numbers. Since √7 exists on the number line and is not an imaginary number (which involve the square root of negative numbers), it is classified as a real number.
Is 7 an integer yes or no?
Yes, 7 is an integer. An integer is a whole number that can be positive, negative, or zero. Since 7 is a whole number and not a fraction or a decimal, it falls under the category of integers.
What is the square root of 7 between?
The square root of 7 lies between the integers 2 and 3. While the exact value of √7 is approximately 2.645751311, it’s important to note that it falls between the perfect squares of 2 (which is 4) and 3 (which is 9). Therefore, we can say that the square root of 7 is greater than 2 but less than 3.
Share :
