Square & Square Root of 73
Square & Square Root of 73
Square of 73
A square number results from multiplying an integer by itself. The square of 73 is 5329. In mathematics, square numbers exhibit distinct properties, crucial for understanding algebraic relationships and patterns. Exploring the square of 73 unveils fundamental principles, enriching comprehension of mathematical structures and operations.
Square Root of 73
The square root, a fundamental concept in mathematics, reveals the number that, when multiplied by itself, yields the original number. The square root of 73 is approximately 8.544. Understanding square roots elucidates the properties and relationships underlying numbers, offering insights into the square of 73 and its mathematical significance.
Is the Square Root of 73 Rational or Irrational?
Irrational number means it cannot be expressed as a simple fraction (ratio of two integers) and its decimal representation is non-repeating and non-terminating.
A rational number is any number that can be expressed as a fraction, where the numerator and denominator are integers, and the denominator is not zero.
Methods to Find Value of Root 73
Estimation Method:
Approximate the square root of 73 by finding the perfect squares closest to it, which are 64 (8²) and 81 (9²).
Since 73 lies between 64 and 81, the square root of 73 is approximately between 8 and 9.
Using a Calculator:
- Directly input √73 into a calculator to get the approximate value.
Babylonian Method (Iterative):
Start with an initial guess, say (x₀ = 8).
Use the iteration formula (xₙ₊₁ =1/2( xₙ + 73/xₙ).
Iterate until the result converges to a desired level of accuracy.
Prime Factorization Method:
Factorize 73 into its prime factors.
Group the factors into pairs and take one factor from each pair outside the square root.
This method is less practical for non-perfect square numbers like 73.
Square Root of 73 by Long Division Method
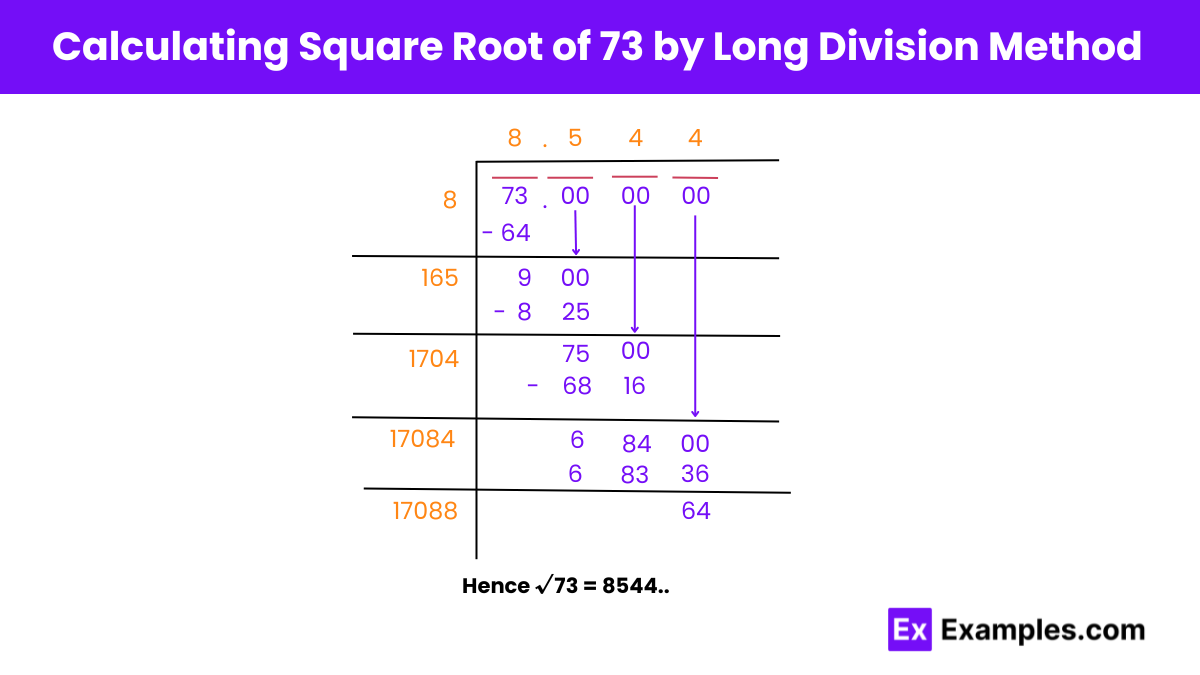
Step 1: We pair digits of a given number starting with a digit at one’s place. Put a horizontal bar to indicate pairing.
Step 2: Now we find a number which on multiplication with itself gives a product less than or equal to 73. As we know 8 × 8 = 64 < 73. Hence, their difference gives 9 and the quotient is 8.
Step 3:Now, we have to bring down 00 and multiply the quotient by 2. This give us 16. Hence, 16 is the starting digit of the new divisor.
Step 4: 5 is placed at one’s place of new divisor because when 165 is multiplied by 5 we get 825. The obtained answer now is 75 and we bring down 00.
Step 5: The quotient now becomes 85 and it is multiplied by 2. This gives 170, which then would become the starting digit of the new divisor.
Step 6: 4 is placed at one’s place of new divisor because on multiplying 1704 by 4 we get 6816. The new divisor now becomes 684 and we bring 00 down.
Step 7: Now the quotient is 854. When multiplied by 2, it gives 1708, which will be the starting digit of the new divisor.
Step 8: 4 is placed at one’s place of the divisor because on multiplying 17084 by 4 we will get 68336. So, now the divisor is 64.
Is 73 Perfect Square root or Not
A perfect square is the square of an integer, and since there is no integer n such that n×n=73, 73 is not a perfect square.
FAQs
Which number is closest to square root 73?
The number closest to the square root of 73 is 8. This is because the square root of 73 is approximately 8.544, and 8 is the nearest whole number to this value.
Can 73 be expressed as the square of an integer?
No, 73 cannot be expressed as the square of an integer, making it a non-perfect square.
How do you simplify the square root of 73?
The square root of 73 cannot be simplified further because it is an irrational number.
What is the decimal approximation of the square root of 73?
The decimal approximation of the square root of 73 is approximately 8.544.
Is the square root of 73 a prime number?
No, the square root of 73 is not a prime number because it is not an integer. The square root of 73 is an irrational number approximately equal to 8.544.
Share :
