Square & Square Root of 784

In the realm of mathematics, especially in algebra, squares and square roots play a crucial role. Squaring a number, as shown by multiplying 784 by itself to yield 614,656, is fundamental. This operation explores properties of rational and irrational numbers, enhancing understanding of mathematical relationships and patterns, crucial for advanced mathematical insights.

Square of 784

784²(784 × 784) = 614656

The square of 784 is calculated by multiplying the number by itself, resulting in 614,656. This calculation (784 squared = 784 × 784) demonstrates how squaring amplifies the magnitude of a number, reflecting its exponential increase in mathematical and practical applications.

Square Root of 784

√784 = 28

The square root of 784 is 28, which is derived by identifying the number that, when multiplied by itself, equals 784. This calculation is straightforward since 784 is a perfect square, formed from 28 squared (28 × 28 = 784). Understanding this helps in solving equations and understanding mathematical concepts that involve square roots and their properties.

Square Root of 784: 28

Exponential Form of 784: (784)½ or  or (784)0.5 

Radical Form of 784: √784

Is the Square Root of 784 Rational or Irrational?

The square root of 784 is rational.

The square root of 784 is a rational number. This classification is based on the ability to express a number as a fraction where both the numerator and the denominator are integer, and the denominator is not zero.

Rational Numbers

A rational number is considered if it can be written as a fraction 𝑝/𝑞​, where 𝑝 and 𝑞 are integers and 𝑞 is not zero. The square root of 784, which is 28, fits this definition perfectly because it can be expressed as 28/1​.

Irrational Numbers

In contrast, an irrational number cannot be expressed as a simple fraction. It is a number that has a non-repeating, non-terminating decimal expansion. Examples include 𝜋 and 2​. These numbers cannot be precisely expressed as a fraction of two integers. The square root of 784, being 28, does not fall into this category, as it can be precisely expressed as a fraction.

Method to Find Value of Root 784

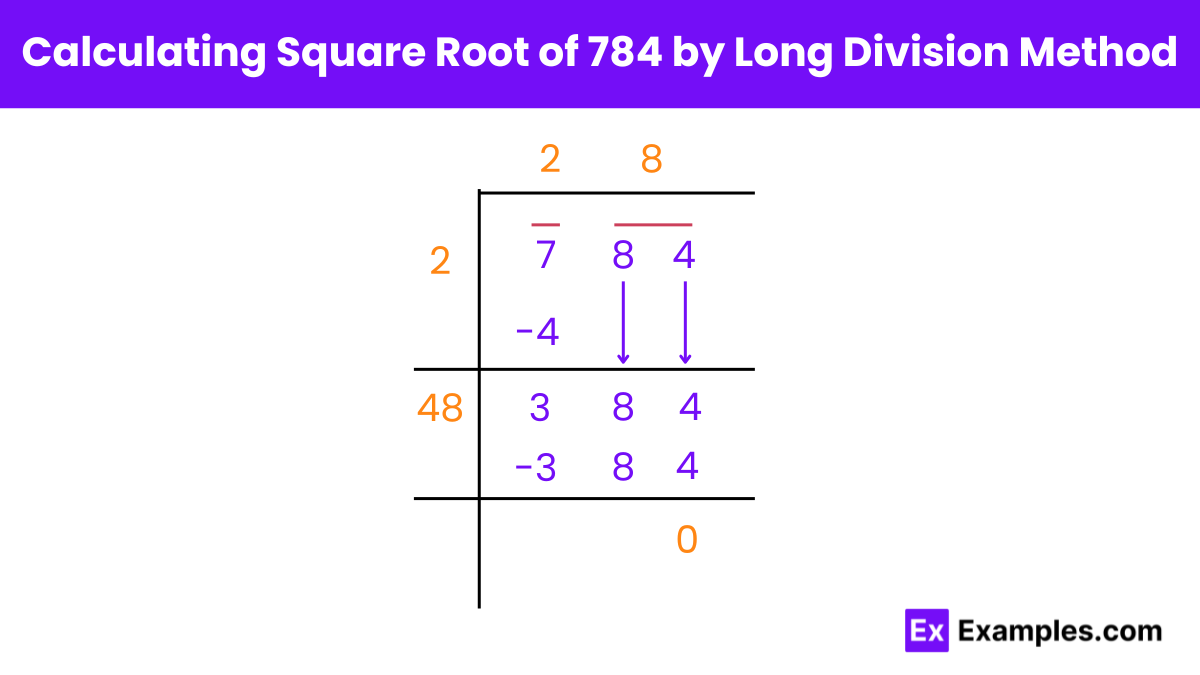
Finding the square root of a number involves determining the value that, when multiplied by itself, gives the original number. For example, the square root of 784 is the value that, when multiplied by itself, equals 784. There are various methods to find the square root of a number, ranging from simple arithmetic techniques to more complex mathematical algorithms.

1. Prime Factorization: Express 784 as a product of prime numbers (2 × 2 × 2 × 2 × 7 × 7), then take one factor from each pair of identical primes, giving you the square root of 784 as 22×7=28

2. Repeated Subtraction: Start with a number close to the square root of 784 (e.g., 27). Subtract it from 784 and adjust the number based on the result until you get 0. This iterative process yields the square root, which is 28.

3. Guess and Check: Estimate the square root of 784 (e.g., 27 or 29) and square it. Adjust your guess based on whether the result is too high or too low until you find the correct value, which is 28.

4. Using a Calculator: Simply input √784 into a calculator, and it will give you the result directly, which is 28.

5. Geometric Method: Draw a square with an area of 784 square units. Then, find the side length of the square, which is the square root of 784, giving you a value of 28 units.

6. Binomial Theorem: Expand (𝑎+𝑏)²=784, where 𝑎=𝑏. Solving this equation yields a value of 𝑎=28, which is the square root of 784.

Using Tables: Refer to precomputed tables of square roots to find the value corresponding to 784, which is 28.

Square Root of 784 by Long Division Method

1. Pair the digits from right to left:
   • Start by pairing the digits of 784. Since it’s a three-digit number, you pair them as 7 and 84.
2. Find the largest number whose square is less than or equal to the first pair:
   • Here, the first pair is 7. The largest whole number whose square is less than or equal to 7 is 2, because 2² = 4.
3. Subtract the square of the number found from the first pair and bring down the next pair:
   • Subtract 4 (which is 2²) from 7, you get 3. Now bring down the next pair, which is 84, making it 384.
4. Double the divisor and choose a new digit in the dividend:
   • The divisor now is 2. Double it to make it 4. Now, you need to find a digit ‘X’ such that (40 + X)X is less than or equal to 384.
5. Find the next digit:
   • (40 + X)X = 384, X = 8 works because 48 × 8 = 384.
6. Subtract and find the remainder:
   • Subtract 384 from 384, and the remainder is 0.
7. Repeat if needed:
   • Since the remainder is 0 and there are no more digits to bring down, the division process stops here.

784 is Perfect Square root or Not?

Yes, 784 is a perfect square

Yes, 784 is a perfect square. It is the square of 28, as 28×28=78428×28=784. When a number can be expressed as the product of an integer with itself, it is referred to as a perfect square. In this case, 784 meets that criteria perfectly.

FAQS

Can the square root of 784 be a negative number?

Yes, the square root of any positive real number has two values: one positive and one negative. Thus, the square root of 784 can also be -28, although the principal square root (commonly referred to in most contexts) is 28.

What are the uses of squares and square roots in real life?

Squares and square roots are used in real life for various purposes, such as computing areas, architectural design, in physics for calculations involving laws of motion and energy, and in statistics for calculating standard deviations.

How can errors occur when calculating the square root of 784 manually?

Errors can occur due to incorrect pairing of digits, mistakes in subtraction, choosing the wrong digit in the long division method, or simply due to miscalculations at any step. Accuracy in each step is crucial to ensure the correct result.

What are some mathematical properties of the number 784?

784 is an even number, and it is divisible by several numbers: 1, 2, 4, 7, 8, 14, 16, 28, 49, 56, 98, 112, 196, 392, and 784. It’s also the product of 24×7224×72, making it a rich number in terms of factors.