What is the value of sin(90∘)?
0
0.5
1
-1
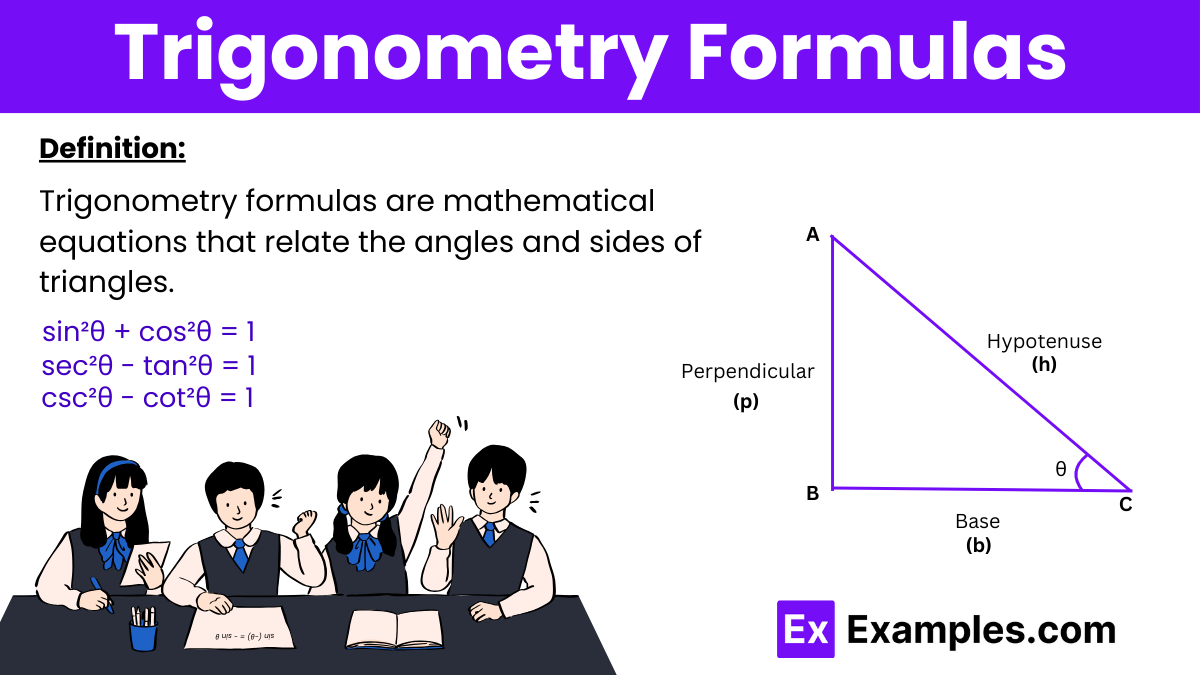
Trigonometry formulas are mathematical equations that relate the angles and sides of triangles. These formulas are essential for solving problems in various fields, including physics, engineering, and architecture. Key trigonometric formulas include the sine, cosine, and tangent functions.
Basic trigonometry formulas establish the relationship between trigonometric ratios and the corresponding sides of a right-angled triangle. There are six primary trigonometric ratios, also known as trigonometric functions: sine, cosine, secant, cosecant, tangent, and cotangent. These functions are abbreviated as sin, cos, sec, csc, tan, and cot, respectively. These functions and identities are derived using a right-angled triangle as the reference.
Cosecant, secant, and cotangent are the reciprocals of the basic trigonometric ratios: sine, cosine, and tangent, respectively. These reciprocal identities are derived from the properties of a right-angled triangle and play a crucial role in trigonometry. They are often used to simplify and solve trigonometric problems. The formulas for these reciprocal trigonometric identities, which are essential for various calculations and transformations in trigonometry, are:
The Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse (ccc) is equal to the sum of the squares of the other two sides (aaa and bbb). Mathematically, this is expressed as: c² = a² + b² ,Using this theorem, we can derive Pythagorean identities in trigonometry, which allow us to convert one trigonometric ratio into another. These identities are fundamental in simplifying and solving trigonometric equations.
These formulas are used to shift the angles by π/2, π, 2π, etc. They are also called co-function identities.

Quadrant I
Quadrant II
Quadrant III
Quadrant IV

sin(−θ) = −sin θ
cos(−θ) = cos θ
tan(−θ) = −tan θ
cosec(−θ) = −cosecθ
sec(−θ) = sec θ
cot(−θ) = −cot θ
sin x sin y = 1/2 [cos(x–y) − cos(x+y)]
cos x cos y = 1/2[cos(x–y) + cos(x+y)]
sin x cos y = 1/2[sin(x+y) + sin(x−y)]
cos x sin y = 1/2[sin(x+y) – sin(x−y)]
sin x + sin y = 2 sin [(x+y)/2] cos [(x-y)/2]
sin x – sin y = 2 cos [(x+y)/2] sin [(x-y)/2]
cos x + cos y = 2 cos [(x+y)/2] cos [(x-y)/2]
cos x – cos y = -2 sin [(x+y)/2] sin [(x-y)/2]
sin² A + cos² A = 1
1+tan² A = sec² A
1+cot² A = cosec² A
| Quadrants→ | I | II | III | IV |
| Sin A | + | + | – | – |
| Cos A | + | – | – | + |
| Tan A | + | – | + | – |
| Cot A | + | – | + | – |
| Sec A | + | – | – | + |
| Cosec A | + | + | – | – |

Here are the domain and range of basic trigonometric functions:
Problem: In a right-angled triangle, if one angle is 30⁰ and the hypotenuse is 10 units, find the length of the side opposite the 30⁰ angle.
Solution:
Problem: In a right-angled triangle, if the adjacent side to the angle θ is 8 units and the hypotenuse is 10 units, find θ
Solution:
Problem: Given that sinθ = 3/5, find cosθ using the Pythagorean identity.
Solution:
Identify the Pythagorean identity: sin²θ+cos²θ=1
Plug in the values: (3/2)² + cos²θ = 1
Solve for cos²θ: (3/2)² = 9/5
9/5+cos²θ = 1
cos²θ = 1− 9/5 = 16/25
cosθ = ± √(16/25) = ±(4/5)
Break down problems into steps, memorize basic formulas, and use mnemonic devices like SOH CAH TOA. Practice regularly with simple problems before advancing to complex ones. Visual aids and triangle diagrams can also help in understanding trigonometric concepts.
Use trigonometric ratios: sine, cosine, and tangent. For any right-angled triangle, apply SOH CAH TOA to find unknown sides or angles. For non-right triangles, use the sine rule or cosine rule. Practice with problems to improve calculation skills.
SOH CAH TOA is a mnemonic to remember trigonometric ratios:
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
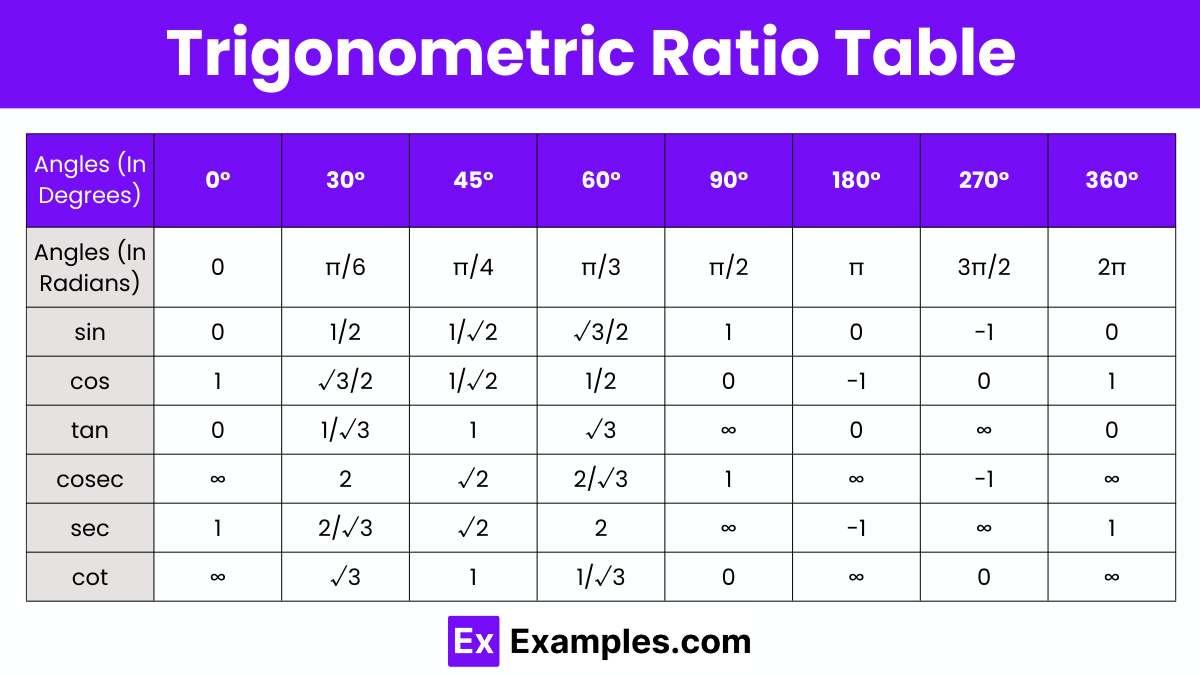
Use trigonometric tables or known values for specific angles (like 30°, 45°, 60°). For exact values, remember special triangles and key trigonometric identities. Practice mental math and estimation for other angles.
Use SOH CAH TOA for right triangles. For non-right triangles, remember the sine rule
(a/sinA=b/sinB=c/sinC)and cosine rule (c² = a² + b² – 2ab cosC)
To solve for tangent (tanθ)
Identify the opposite and adjacent sides.
Use the formula tan θ = Opposite/adjacent
Plug in the values and simplify.
In a right-angled triangle, use the Pythagorean theorem:
Hypotenuse= √(opposite²+adjacent²)
Or, use trigonometric ratios if an angle and a side are known.
In a 30-60-90 triangle, the sides have a consistent ratio:
Shortest side (opposite 30°) = x
Hypotenuse (opposite 90°) = 2x
Longest side (opposite 60°) = x √3
The angle of depression is the angle between the horizontal line and the line of sight looking downward. It is equal to the angle of elevation from the observer’s point of view on the ground.
Identify known sides or angles. Use SOH CAH TOA for trigonometric ratios:
Sine = opposite/hypotenuse
Cosine = adjacent/hypotenuse
Tangent = opposite/adjacent Apply the Pythagorean theorem as needed.
In a 45-45-90 triangle, the sides are in a ratio of 1:1:: √2:
Both legs are equal.
Hypotenuse = leg x √2

Trigonometry formulas are mathematical equations that relate the angles and sides of triangles. These formulas are essential for solving problems in various fields, including physics, engineering, and architecture. Key trigonometric formulas include the sine, cosine, and tangent functions.
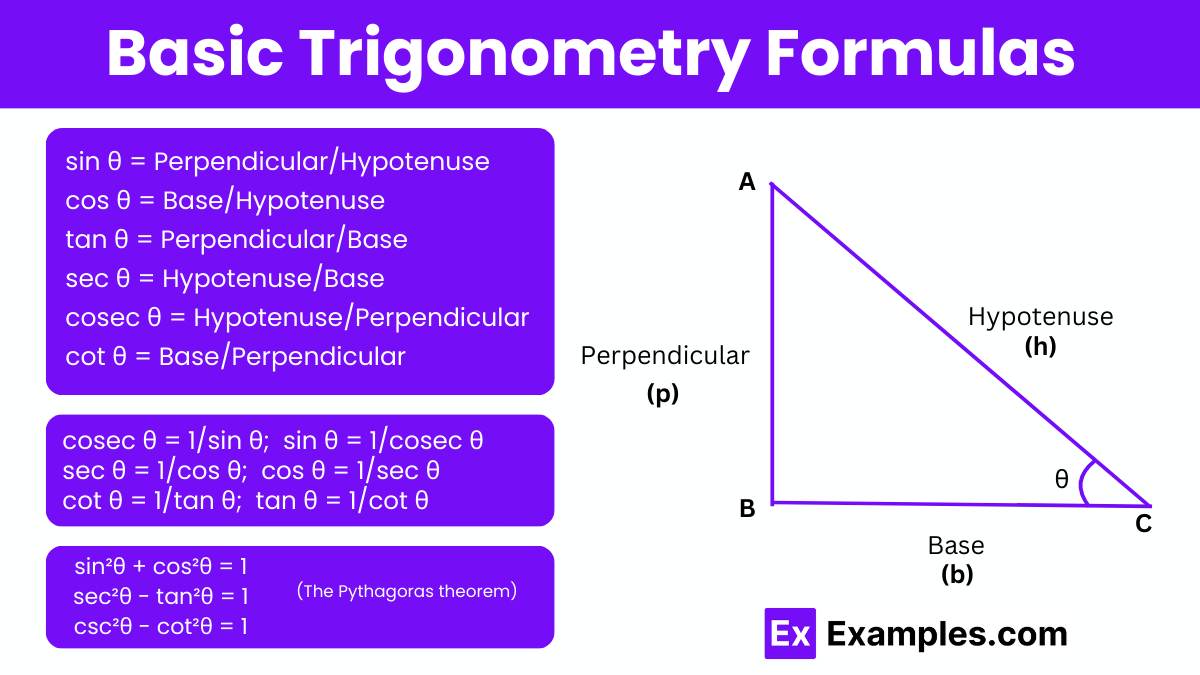
Basic trigonometry formulas establish the relationship between trigonometric ratios and the corresponding sides of a right-angled triangle. There are six primary trigonometric ratios, also known as trigonometric functions: sine, cosine, secant, cosecant, tangent, and cotangent. These functions are abbreviated as sin, cos, sec, csc, tan, and cot, respectively. These functions and identities are derived using a right-angled triangle as the reference.

Download All Trigonometry Formulas
sin θ = Perpendicular/Hypotenuse
cos θ = Base/Hypotenuse
tan θ = Perpendicular/Base
sec θ = Hypotenuse/Base
cosec θ = Hypotenuse/Perpendicular
cot θ = Base/Perpendicular
Cosecant, secant, and cotangent are the reciprocals of the basic trigonometric ratios: sine, cosine, and tangent, respectively. These reciprocal identities are derived from the properties of a right-angled triangle and play a crucial role in trigonometry. They are often used to simplify and solve trigonometric problems. The formulas for these reciprocal trigonometric identities, which are essential for various calculations and transformations in trigonometry, are:
cosec θ = 1/sin θ; sin θ = 1/cosec θ
sec θ = 1/cos θ; cos θ = 1/sec θ
cot θ = 1/tan θ; tan θ = 1/cot θ
The Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse (ccc) is equal to the sum of the squares of the other two sides (aaa and bbb). Mathematically, this is expressed as: c² = a² + b² ,Using this theorem, we can derive Pythagorean identities in trigonometry, which allow us to convert one trigonometric ratio into another. These identities are fundamental in simplifying and solving trigonometric equations.
sin²θ + cos²θ = 1
sec²θ – tan²θ = 1
csc²θ – cot²θ = 1

These formulas are used to shift the angles by π/2, π, 2π, etc. They are also called co-function identities.
sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
sin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A
sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
sin (π – A) = sin A & cos (π – A) = – cos A
sin (π + A) = – sin A & cos (π + A) = – cos A
sin (2π – A) = – sin A & cos (2π – A) = cos A
sin (2π + A) = sin A & cos (2π + A) = cos A
sin(90°−x) = cos x
cos(90°−x) = sin x
tan(90°−x) = cot x
cot(90°−x) = tan x
sec(90°−x) = cosec x
cosec(90°−x) = sec x
sin(x+y) = sin(x)cos(y)+cos(x)sin(y)
cos(x+y) = cos(x)cos(y)–sin(x)sin(y)
𝑡𝑎𝑛(𝑥+𝑦)= (𝑡𝑎𝑛 𝑥+𝑡𝑎𝑛𝑦) / (1−𝑡𝑎𝑛 𝑥.𝑡𝑎𝑛 𝑦)
sin(x–y) = sin(x)cos(y)–cos(x)sin(y)
cos(x–y) = cos(x)cos(y) + sin(x)sin(y)
tan(x-y) = (tan x – tan y) (1+tan x.tan y)
Sin 3x = 3sin x – 4sin³x
Cos 3x = 4cos³x-3cos x
Tan 3x = (3tanx – tan³x)/(1-3tan²x)
sin⁻¹ (–x) = – sin⁻¹ x
cos⁻¹ (–x) = π – cos⁻¹ x
tan⁻¹ (–x) = – tan⁻¹ x
cosec⁻¹ (–x) = – cosec⁻¹ x
sec⁻¹ (–x) = π – sec⁻¹ x
cot⁻¹ (–x) = π – cot⁻¹ x
sin (-θ) = − sin θ
cos (−θ) = cos θ
tan (−θ) = − tan θ
cosec (−θ) = − cosec θ
sec (−θ) = sec θ
cot (−θ) = − cot θ

sin (-θ) = − sin θ
cos (−θ) = cos θ
tan (−θ) = − tan θ
cosec (−θ) = − cosec θ
sec (−θ) = sec θ
cot (−θ) = − cot θ
sin²A + cot²A = 1
tan²A + 1 = sec²A
cot²A + 1 = cosec²A
sin(2nπ + θ ) = sin θ
cos(2nπ + θ ) = cos θ
tan(2nπ + θ ) = tan θ
cot(2nπ + θ ) = cot θ
sec(2nπ + θ ) = sec θ
cosec(2nπ + θ ) = cosec θ
Quadrant I
sin(π/2 − θ) = cos θ
cos(π/2 − θ) = sin θ
tan(π/2 − θ) = cot θ
cot(π/2 − θ) = tan θ
sec(π/2 − θ) = cosec θ
cosec(π/2 − θ) = sec θ
Quadrant II
sin(π − θ) = sin θ
cos(π − θ) = -cos θ
tan(π − θ) = -tan θ
cot(π − θ) = – cot θ
sec(π − θ) = -sec θ
cosec(π − θ) = cosec θ
Quadrant III
sin(π + θ) = – sin θ
cos(π + θ) = – cos θ
tan(π + θ) = tan θ
cot(π + θ) = cot θ
sec(π + θ) = -sec θ
cosec(π + θ) = -cosec θ
Quadrant IV
sin(2π − θ) = – sin θ
cos(2π − θ) = cos θ
tan(2π − θ) = – tan θ
cot(2π − θ) = – cot θ
sec(2π − θ) = sec θ
cosec(2π − θ) = -cosec θ
sin (A + B) = sin A cos B + cos A sin B
sin (A − B) = sin A cos B – cos A sin B
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
tan(A + B) = [(tan A + tan B)/(1 – tan A tan B)]
tan(A – B) = [(tan A – tan B)/(1 + tan A tan B)]
sin 2A = 2 sin A cos A = [2 tan A /(1 + tan²A)]
cos 2A = cos²A – sin²A = 1 – 2 sin²A = 2 cos²A – 1 = [(1 – tan²A)/(1 + tan²A)]
tan 2A = (2 tan A)/(1 – tan2A)
sin 3A = 3 sinA – 4 sin³A
cos 3A = 4 cos³A – 3 cos A
tan 3A = [3 tan A – tan³A]/[1 − 3 tan²A]

sin(−θ) = −sin θ
cos(−θ) = cos θ
tan(−θ) = −tan θ
cosec(−θ) = −cosecθ
sec(−θ) = sec θ
cot(−θ) = −cot θ
sin x sin y = 1/2 [cos(x–y) − cos(x+y)]
cos x cos y = 1/2[cos(x–y) + cos(x+y)]
sin x cos y = 1/2[sin(x+y) + sin(x−y)]
cos x sin y = 1/2[sin(x+y) – sin(x−y)]
sin x + sin y = 2 sin [(x+y)/2] cos [(x-y)/2]
sin x – sin y = 2 cos [(x+y)/2] sin [(x-y)/2]
cos x + cos y = 2 cos [(x+y)/2] cos [(x-y)/2]
cos x – cos y = -2 sin [(x+y)/2] sin [(x-y)/2]
sin² A + cos² A = 1
1+tan² A = sec² A
1+cot² A = cosec² A
Quadrants→ | I | II | III | IV |
Sin A | + | + | – | – |
Cos A | + | – | – | + |
Tan A | + | – | + | – |
Cot A | + | – | + | – |
Sec A | + | – | – | + |
Cosec A | + | + | – | – |

Here are the domain and range of basic trigonometric functions:
Sine function, sine: R → [– 1, 1]
Cosine function, cos : R → [– 1, 1]
Tangent function, tan : R – { x : x = (2n + 1) π/2, n ∈ Z} →R
Cotangent function, cot : R – { x : x = nπ, n ∈ Z} →R
Secant function, sec : R – { x : x = (2n + 1) π/2, n ∈ Z} →R – (– 1, 1)
Cosecant function, cosec : R – { x : x = nπ, n ∈ Z} →R – (– 1, 1)
sin⁻¹ (1/a) = cosec⁻¹(a), a ≥ 1 or a ≤ – 1
cos⁻¹(1/a) = sec⁻¹(a), a ≥ 1 or a ≤ – 1
tan⁻¹(1/a) = cot⁻¹(a), a>0
sin⁻¹(–a) = – sin⁻¹(a), a ∈ [– 1, 1]
tan⁻¹(–a) = – tan⁻¹(a), a ∈ R
cosec⁻¹(–a) = –cosec⁻¹(a), | a | ≥ 1
cos⁻¹(–a) = π – cos⁻¹(a), a ∈ [– 1, 1]
sec⁻¹(–a) = π – sec⁻¹(a), | a | ≥ 1
cot⁻¹(–a) = π – cot⁻¹(a), a ∈ R
sin⁻¹a + cos⁻¹a = π/2, a ∈ [– 1, 1]
tan⁻¹a + cot⁻¹a = π/2, a ∈ R
cosec⁻¹a + sec⁻¹a = π/2, | a | ≥ 1
tan⁻¹a + tan⁻¹ b = tan⁻¹ [(a+b)/1-ab], ab<1
tan⁻¹a – tan⁻¹ b = tan⁻¹ [(a-b)/1+ab], ab>-1
tan⁻¹a – tan⁻¹ b = π + tan⁻¹[(a+b)/1-ab], ab > 1; a,b > 0
2tan⁻¹a = sin⁻¹ [2a/(1+a²)], |a| ≤ 1
2tan⁻¹a = cos⁻¹[(1-a²)/(1+a²)], a ≥ 0
2tan⁻¹a = tan⁻¹[2a/(1+a²)], – 1 < a < 1
Problem: In a right-angled triangle, if one angle is 30⁰ and the hypotenuse is 10 units, find the length of the side opposite the 30⁰ angle.
Solution:
Identify the formula: sinθ = opposite/hypotenuse
Plug in the values: sin30⁰ = opposite/10
Solve for the opposite side: sin30⁰=1/2
=>1/2=opposite/10
Opposite = 10 x 1/2 = 5 units
Problem: In a right-angled triangle, if the adjacent side to the angle θ is 8 units and the hypotenuse is 10 units, find θ
Solution:
Identify the formula: cosθ = adjacent/hypotenuse
Plug in the values: cosθ = 8/10
Simplify the fraction: cosθ=4/5 = 0.8
Use the inverse cosine function to find θ:
θ = cos⁻¹(0.8)≈36.87⁰
Problem: Given that sinθ = 3/5, find cosθ using the Pythagorean identity.
Solution:
Identify the Pythagorean identity: sin²θ+cos²θ=1
Plug in the values: (3/2)² + cos²θ = 1
Solve for cos²θ: (3/2)² = 9/5
9/5+cos²θ = 1
cos²θ = 1− 9/5 = 16/25
cosθ = ± √(16/25) = ±(4/5)
Break down problems into steps, memorize basic formulas, and use mnemonic devices like SOH CAH TOA. Practice regularly with simple problems before advancing to complex ones. Visual aids and triangle diagrams can also help in understanding trigonometric concepts.
Use trigonometric ratios: sine, cosine, and tangent. For any right-angled triangle, apply SOH CAH TOA to find unknown sides or angles. For non-right triangles, use the sine rule or cosine rule. Practice with problems to improve calculation skills.
SOH CAH TOA is a mnemonic to remember trigonometric ratios:
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
Use trigonometric tables or known values for specific angles (like 30°, 45°, 60°). For exact values, remember special triangles and key trigonometric identities. Practice mental math and estimation for other angles.
Use SOH CAH TOA for right triangles. For non-right triangles, remember the sine rule
(a/sinA=b/sinB=c/sinC)and cosine rule (c² = a² + b² – 2ab cosC)
To solve for tangent (tanθ)
Identify the opposite and adjacent sides.
Use the formula tan θ = Opposite/adjacent
Plug in the values and simplify.
In a right-angled triangle, use the Pythagorean theorem:
Hypotenuse= √(opposite²+adjacent²)
Or, use trigonometric ratios if an angle and a side are known.
In a 30-60-90 triangle, the sides have a consistent ratio:
Shortest side (opposite 30°) = x
Hypotenuse (opposite 90°) = 2x
Longest side (opposite 60°) = x √3
The angle of depression is the angle between the horizontal line and the line of sight looking downward. It is equal to the angle of elevation from the observer’s point of view on the ground.
Identify known sides or angles. Use SOH CAH TOA for trigonometric ratios:
Sine = opposite/hypotenuse
Cosine = adjacent/hypotenuse
Tangent = opposite/adjacent Apply the Pythagorean theorem as needed.
In a 45-45-90 triangle, the sides are in a ratio of 1:1:: √2:
Both legs are equal.
Hypotenuse = leg x √2
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the value of sin(90∘)?
0
0.5
1
-1
Which of the following is the formula for the Pythagorean identity?
sin²θ + cos²θ = 1
sin²θ - cos²θ = 1
tan²θ + 1 = sec²θ
sinθ⋅cosθ=0
The formula for the sine of a sum of angles is given by:
\sin(A + B) = \sin A \cos B + \cos A \sin B
\sin(A + B) = \sin A \sin B + \cos A \cos B
\sin(A + B) = \sin A + \sin B
\sin(A + B) = \cos A \cos B - \sin A \sin B
What is the cosine of 0^\circ?
0
0.5
1
-1
Which identity is used to express \cos(2\theta) in terms of \cos \theta?
\cos(2\theta) = 2 \cos^2 \theta - 1
\cos(2\theta) = 1 - 2 \sin^2 \theta
\cos(2\theta) = \sin^2 \theta - \cos^2 \theta
\cos(2\theta) = \cos^2 \theta - \sin^2 \theta
The tangent of an angle \theta is the ratio of:
\sin \theta to \cos \theta
\cos \theta to \sin \theta
\sin \theta to \cot \theta
\cos \theta to \cot \theta
What is the secant of 90^\circ?
0
1
Undefined
\sqrt{2}
The formula for \sin^2 \theta can also be expressed as:
\frac{1 - \cos 2\theta}{2}
\frac{1 + \cos 2\theta}{2}
\frac{1 - \sin 2\theta}{2}
\frac{1 + \sin 2\theta}{2}
Which of the following is the correct formula for converting radians to degrees?
Degrees = Radians × \frac{180}{\pi}
Degrees = Radians × \frac{\pi}{180}
Degrees = Radians × \pi
Degrees = Radians ÷ \pi
The formula for \sin(\theta) + \sin(\phi) is given by:
\sin(\theta) + \sin(\phi) = \sin(\theta + \phi)
\sin(\theta) + \sin(\phi) = \sin(\theta) \cos(\phi) + \cos(\theta) \sin(\phi)
\sin(\theta) + \sin(\phi) = 2 \sin(\theta + \phi)
\sin(\theta) + \sin(\phi) = 2 \sin\left(\frac{\theta + \phi}{2}\right) \cos\left(\frac{\theta - \phi}{2}\right)
Before you leave, take our quick quiz to enhance your learning!

