Fluids in motion

Fluids in motion are essential to understanding how liquids and gases behave under various forces and conditions. On the MCAT, you’ll explore key principles like continuity, Bernoulli’s equation, and the effects of pressure changes. Understanding laminar and turbulent flow, viscosity, and fluid dynamics is crucial, as these concepts play a vital role in mastering the physics and biochemistry sections of the exam.

Learning Objectives

In studying “Fluids in Motion” for the MCAT, you should learn to uViscosity and Fluid Resistance in Biological Systemsnderstand the principles governing fluid dynamics, including concepts such as laminar and turbulent flow. Analyze the relationship between pressure, velocity, and elevation using Bernoulli’s equation. Apply the continuity equation to explore how fluid flow rate remains constant in an incompressible fluid. Evaluate factors affecting viscosity and how it influences fluid resistance in biological systems. Understand the concept of Poiseuille’s law for flow through narrow tubes and how it relates to blood circulation. Examine the role of hydrostatic pressure in fluid systems and the importance of Reynolds number in predicting flow patterns. Additionally, develop proficiency in identifying and solving MCAT problems related to fluid motion, including applications in respiratory and cardiovascular physiology.

Principles of Fluid Dynamics: Laminar and Turbulent Flow

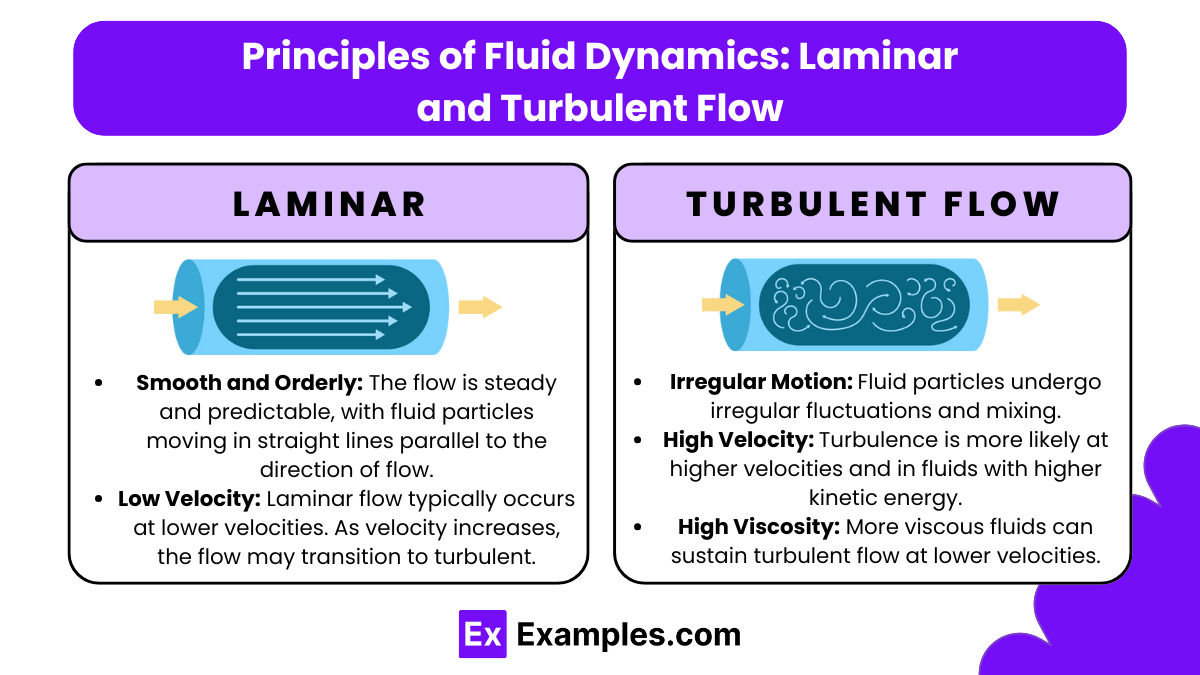
Laminar Flow

Laminar flow, also known as streamline flow, occurs when a fluid flows in parallel layers, with no disruption between the layers. This type of flow is characterized by smooth and orderly movement of fluid particles along well-defined paths or streamlines. Each layer of fluid slides past adjacent layers with little to no mixing.

Characteristics of Laminar Flow:

• Smooth and Orderly: The flow is steady and predictable, with fluid particles moving in straight lines parallel to the direction of flow.
• Low Velocity: Laminar flow typically occurs at lower velocities. As velocity increases, the flow may transition to turbulent.
• Low Viscosity: Fluids with low viscosity (e.g., water, air) are more prone to laminar flow at lower velocities.
• Reynolds Number: Laminar flow is generally observed when the Reynolds number, a dimensionless number used to predict flow patterns in fluid dynamics, is less than 2000.

Applications of Laminar Flow:

• Microfluidics: Used in devices where precise control over fluid movement is necessary.
• Lubrication: The laminar flow of oil between moving parts reduces wear and dissipates heat.
• Medical and Biotechnological Applications: For example, laminar airflow in cleanrooms prevents cross-contamination by ensuring air moves in a single direction at a uniform speed.

Turbulent Flow

Turbulent flow is characterized by chaotic and irregular fluid motion. In turbulent flow, the speed of the fluid at a point can vary erratically; vortices, eddies, and other flow instabilities are common.

Characteristics of Turbulent Flow:

• Irregular Motion: Fluid particles undergo irregular fluctuations and mixing.
• High Velocity: Turbulence is more likely at higher velocities and in fluids with higher kinetic energy.
• High Viscosity: More viscous fluids can sustain turbulent flow at lower velocities compared to less viscous ones.
• Reynolds Number: Turbulent flow typically occurs when the Reynolds number is greater than 4000. Between 2000 and 4000, the flow is transitional, showing characteristics of both types.

Applications of Turbulent Flow:

• Mixing and Chemical Reactions: Turbulent flow enhances mixing and increases the rate of chemical reactions.
• Heat Transfer: The chaotic movement of fluid particles in turbulent flow increases the rate of heat transfer, beneficial in many industrial processes.
• Meteorology: The study of atmospheric turbulence is vital for understanding weather patterns and predicting storms.

Transition from Laminar to Turbulent Flow

The transition from laminar to turbulent flow is influenced by factors such as velocity, fluid density, and viscosity, and is typically characterized by an increasing Reynolds number. This transition is critical in many engineering applications, where the type of flow can affect the efficiency and safety of systems.

For example, in cardiovascular health, laminar blood flow is ideal within blood vessels because it is less likely to cause shear stress and damage to the vessel walls. In contrast, turbulent blood flow can contribute to conditions such as atherosclerosis.

Viscosity and Fluid Resistance in Biological Systems

Viscosity in Biological Systems

Viscosity is a measure of a fluid’s resistance to gradual deformation by shear stress or tensile stress. In biological contexts, it refers to the thickness or stickiness of a fluid and its resistance to flow.

• Blood Viscosity: Blood viscosity is crucial for cardiovascular health. High viscosity can increase the workload on the heart and reduce the efficiency of blood flow, potentially leading to clots or vascular diseases. Blood’s viscosity depends on several factors, including the number and size of red blood cells, and the plasma composition.
• Mucus Viscosity: Mucus protects tissues in the respiratory, gastrointestinal, and reproductive systems. Its viscosity determines its effectiveness in trapping pathogens and allergens, and in facilitating or impeding the movement of cells and particles through it.

Fluid Resistance in Biological Systems

Fluid resistance, or drag, refers to forces that oppose the motion of an object through a fluid. This is a key factor in the mobility of aquatic organisms and the function of various bodily fluids.

• Aquatic Locomotion: For organisms swimming in water, such as fish and marine mammals, overcoming water resistance is vital for efficient movement. Adaptations to reduce this resistance include streamlined body shapes and specialized skin textures.
• Airway Resistance: In human respiratory tracts, airway resistance affects how easily air flows in and out of the lungs. This can be influenced by diseases that change the characteristics of airway mucus, such as asthma and cystic fibrosis.

Hydrostatic Pressure in Fluid Systems

Hydrostatic pressure increases linearly with depth due to the weight of the fluid above the point of measurement. It is independent of the shape of the container and depends only on the height of the fluid column, the density of the fluid, and the acceleration due to gravity.

The hydrostatic pressure P at a depth h in a fluid of density ρ can be calculated using the formula:

P₀ = pgh

where:

• P₀​ is the pressure at the fluid surface,
• ρ is the fluid density,
• g is the acceleration due to gravity,
• h is the depth below the surface of the fluid.

Continuity Equation: Conservation of Fluid Flow Rate

The continuity equation states that the flow rate of an incompressible fluid remains constant across a system:

A_1​v₁ ​= A₂​v_2​

• A_1​ and A₂ are the cross-sectional areas of the pipe or channel at two different points.
• v_1​ and v₂​ are the fluid velocities at these points.

For an incompressible fluid, where the density (ρ) remains constant, the equation simplifies the conservation of volume flow rate, indicating that the product of cross-sectional area and velocity at any two points along the streamline is constant.

Example:
If blood flows through a narrowing artery, the velocity must increase to maintain a constant flow rate. For instance, if the area of the artery decreases by half, the velocity doubles.

Applications of the Continuity Equation:

1. Pipe Flow Analysis: In engineering, particularly in systems involving water supply, oil, and gas transport, the continuity equation is used to calculate the velocity of the fluid at different sections of a pipeline when the diameter of the pipe changes. If the pipe narrows, the velocity of the fluid increases, which is a direct application of the continuity equation.

2. Aerodynamics: In aerodynamics, the continuity equation helps understand how air flows around objects. For instance, as air flows over an airplane wing and encounters changes in cross-sectional area, the air velocity changes accordingly. This is crucial for calculating lift and drag forces.

3. Cardiovascular Physics: In medical physics, the continuity equation is used to study blood flow through arteries and veins. Changes in the diameter of blood vessels can significantly affect blood velocity, which is important in diagnosing conditions like arterial stenosis.

4. Environmental Studies: Hydrologists use the continuity equation to model the flow of water in rivers and streams, especially when the river’s width or depth changes. This modeling is critical in flood prediction and management.

5. Meteorology: In meteorology, the continuity equation applies to air movement in weather systems. Variations in atmospheric pressure and temperature can alter air density and velocity, impacting weather patterns and predictions.

Examples

Example 1: Water Flowing Through a Hose

When water is pumped through a garden hose, it experiences motion due to the pressure difference created by the pump. As the water flows, its velocity can change depending on the hose diameter and any restrictions, like a nozzle. This example illustrates how fluids can move efficiently through conduits, affected by factors such as pressure and friction.

Example 2: Airflow Over an Airplane Wing

The movement of air over an airplane wing demonstrates the principles of fluid dynamics in motion. As the airplane moves forward, air flows over and under the wing, creating differences in pressure that generate lift. This motion of air is crucial for flight and is governed by the principles of Bernoulli’s equation, which relates speed and pressure in a fluid.

Example 3: Blood Circulating in the Body

The circulatory system exemplifies fluid motion within biological systems. Blood, a viscous fluid, is pumped by the heart through a network of arteries and veins. The flow rate and pressure within the circulatory system are vital for delivering oxygen and nutrients to tissues and removing waste products, highlighting how fluid motion is essential for sustaining life.

Example 4: Ocean Currents

Large-scale movements of water in the oceans, known as ocean currents, are critical examples of fluids in motion. These currents are driven by factors such as wind, the Earth’s rotation, and differences in water temperature and salinity. Ocean currents play a significant role in climate regulation, marine ecosystems, and navigation, illustrating the complex interactions within fluid dynamics.

Example 5: Smoke Rising from a Fire

The movement of smoke from a fire showcases fluid motion in a gaseous medium. As smoke rises, it carries heat and particulates into the air. The motion of smoke is influenced by convection currents, where warm air rises and cooler air moves in to replace it. This example highlights how temperature differences can drive the motion of fluids and affect the dispersion of gases in the atmosphere.

Practice Questions

Question 1

What is the primary factor that influences the flow rate of a fluid in a pipe?

A) The temperature of the fluid
B) The viscosity of the fluid
C) The color of the fluid
D) The type of pipe material

Correct Answer: B) The viscosity of the fluid.

Explanation: Viscosity is a measure of a fluid’s resistance to flow. A fluid with high viscosity (like honey) flows more slowly than a fluid with low viscosity (like water). Therefore, the viscosity of the fluid is a primary factor influencing how easily it can flow through a pipe. While temperature can affect viscosity and flow rate, it is not the primary determinant. The color of the fluid and the pipe material may affect other characteristics but do not primarily influence flow rate.

Question 2

Which of the following scenarios best demonstrates turbulent flow in a fluid?

A) Water flowing gently from a faucet
B) Oil moving smoothly through a narrow tube
C) Rapids in a river with swirling eddies
D) Air moving steadily over a flat surface

Correct Answer: C) Rapids in a river with swirling eddies.

Explanation: Turbulent flow is characterized by chaotic changes in pressure and flow velocity, often creating eddies and swirls, as seen in rapids. In contrast, laminar flow is smooth and orderly, as seen in water flowing gently from a faucet or oil moving smoothly in a narrow tube. Air moving steadily over a flat surface typically represents laminar flow as well, not turbulence.

Question 3

What happens to the speed of a fluid as it passes through a constricted section of a pipe?

A) The speed decreases.
B) The speed remains constant.
C) The speed increases.
D) The speed becomes unpredictable.

Correct Answer: C) The speed increases.

Explanation: According to the principle of conservation of mass, when a fluid flows through a pipe that narrows (constricted section), the fluid must move faster to maintain a constant flow rate. This principle is often illustrated with the concept of continuity, where the product of the cross-sectional area of the pipe and the fluid velocity remains constant. Therefore, as the area decreases, the speed of the fluid increases to compensate.