Kinetic molecular theory of gases

The kinetic molecular theory of gases is fundamental to understanding gas behavior, providing insight into pressure, temperature, and volume relationships. On the MCAT, you’ll explore gas laws, molecular motion, and ideal versus real gas behavior. Mastering concepts like kinetic energy, the distribution of molecular speeds, and deviations under non-ideal conditions is essential. Understanding these principles helps you excel in the chemistry and physics sections, where gas dynamics are key components.

Learning Objectives

In studying “Kinetic Molecular Theory of Gases” for the MCAT, you should learn to understand the basic assumptions of the theory, including the behavior of gas particles in constant random motion and their negligible volume. Recognize how temperature relates to the average kinetic energy of gas particles and how gas pressure results from collisions with container walls. Analyze the relationships between gas variables using the ideal gas law and understand deviations from ideal behavior at high pressures and low temperatures. Evaluate the role of intermolecular forces and volume corrections in real gases. Additionally, apply the theory to explain diffusion, effusion, and the impact of molecular speed distribution on gas behavior under different conditions.

Kinetic Molecular Theory of Gases

1. Gas Particles are Small and Far Apart: The actual volume occupied by gas molecules is negligibly small compared to the total volume of the gas. This implies that most of the volume of a gas is empty space.
2. Constant Random Motion: Gas particles are in constant, random motion. They move in straight lines until they collide with either another particle or the walls of their container.
3. Elastic Collisions: Collisions between gas particles or between particles and the container walls are perfectly elastic. This means that there is no net loss of kinetic energy from these collisions.
4. No Interactions: There are no attractive or repulsive forces between the particles of an ideal gas. This allows for the simplification of many calculations, though it deviates from reality where such forces can exist, particularly under high pressures and low temperatures.
5. Kinetic Energy and Temperature: The average kinetic energy of gas particles is proportional to the temperature of the gas in kelvins. Higher temperatures correspond to higher average kinetic energies.

Ideal Gas Law and the Relationships Between Gas Variables

The Ideal Gas Law is a fundamental equation in the study of thermodynamics and physical chemistry, summarizing the relationships between the four main physical properties of an ideal gas: pressure, volume, temperature, and the amount of gas. It provides a practical tool for predicting and manipulating the behavior of gases under various conditions.

The Ideal Gas Law Formula

The Ideal Gas Law is usually stated as: PV = nRT where:

• P is the pressure of the gas,
• V is the volume occupied by the gas,
• n is the number of moles of the gas,
• R is the ideal gas constant, and
• T is the temperature of the gas in Kelvin.

Relationships Between Gas Variables

1. Pressure and Volume (Boyle’s Law): At a constant temperature and amount of gas, the pressure and volume of an ideal gas are inversely proportional. This relationship is described by Boyle’s Law: P∝1/V or PV = constant As pressure increases, volume decreases, assuming temperature remains constant.

2. Volume and Temperature (Charles’s Law): At constant pressure, the volume of an ideal gas is directly proportional to its temperature in Kelvin. This is Charles’s Law: V∝T or V/T = constant As temperature increases, so does the volume.

3. Pressure and Temperature (Gay-Lussac’s Law): At constant volume, the pressure of an ideal gas is directly proportional to its temperature: P∝T or P/T = constant This means that as temperature increases, pressure increases when the volume is held fixed.

4. Amount of Gas and Volume (Avogadro’s Law): At constant temperature and pressure, the volume of a gas is directly proportional to the amount of gas (number of moles): V∝n or V/n = constant. This implies that adding more gas, while keeping temperature and pressure constant, increases the volume.

Role of Intermolecular Forces and Volume Corrections in Real Gases

Intermolecular forces are the forces of attraction or repulsion between molecules. In the context of real gases, these forces play a significant role:

Intermolecular Forces

1. Attraction Between Molecules: At moderate to high pressures, the attractive forces between molecules become significant. These attractions reduce the impact of the molecules on the container walls, which in turn lowers the measured pressure compared to what would be expected from the ideal gas law. This is particularly noticeable as a gas approaches its liquefaction point, where the attractive forces begin to dominate behavior, leading to condensation.
2. Repulsion Between Molecules: At very high pressures, the repulsive forces become important. These forces are due to the electron clouds of adjacent molecules repelling each other when molecules are forced very close together. This effect leads to a pressure that is higher than what would be predicted by the ideal gas law.

Volume Corrections for Real Gases

The ideal gas law assumes that the volume occupied by the gas molecules themselves is negligible compared to the container’s volume. However, this assumption fails under high pressures or when the gas is compressed to a small volume:

1. Finite Volume of Molecules: As pressure increases, the finite size of the gas molecules prevents them from being compressed beyond a certain point. This effectively reduces the volume available for molecular motion, increasing the frequency of collisions with the container walls and thus increasing the pressure.
2. Excluded Volume: The volume actually occupied by the gas molecules is termed the excluded volume. This must be subtracted from the total volume of the container to get the volume in which the gas molecules can freely move.

Temperature and the Average Kinetic Energy of Gas Particles

Temperature and the average kinetic energy of gas particles are closely linked concepts central to understanding thermodynamics, particularly in the context of gases. This relationship provides insights into the behavior of gases at the molecular level and forms a foundational component of the kinetic molecular theory.

The Relationship Between Temperature and Kinetic Energy

The average kinetic energy of gas particles is directly proportional to the absolute temperature of the gas. This relationship can be expressed mathematically as: KE_avg = 3/2k_BT where:

• KE_avg​ is the average kinetic energy of the particles in the gas,
• k_B​ is the Boltzmann constant (1.38×10⁻²³ J/K),
• T is the absolute temperature in Kelvin.

1. Kinetic Energy of Particles:

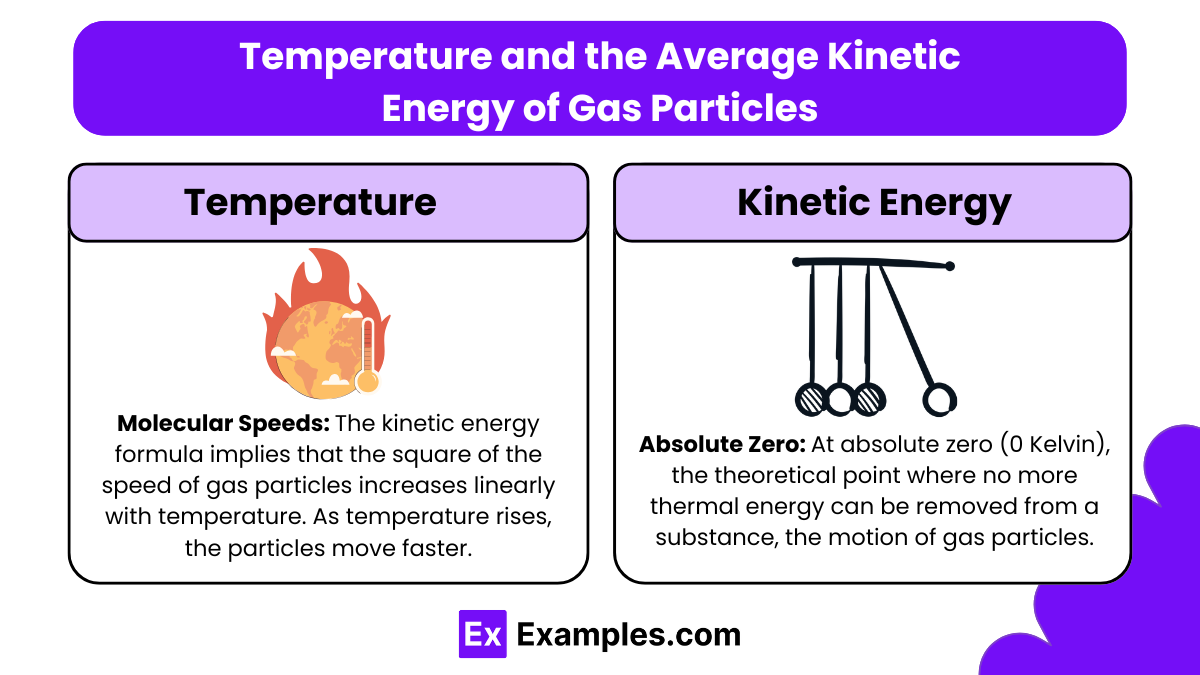
• Molecular Speeds: The kinetic energy formula implies that the square of the speed of gas particles increases linearly with temperature. As temperature rises, the particles move faster. This increase in particle speed is reflected in increased pressure and volume, according to the ideal gas law, assuming the gas is contained in a flexible container or its pressure is not otherwise constrained.

2. Temperature as a Measure of Energy:

• Absolute Zero: At absolute zero (0 Kelvin), the theoretical point where no more thermal energy can be removed from a substance, the motion of gas particles would cease entirely, meaning their kinetic energy would be zero. However, reaching absolute zero is practically impossible.
• Thermal Energy: Temperature is essentially a measure of the average thermal energy or kinetic energy of the particles in a substance. This makes temperature a crucial variable in all fields of science and engineering dealing with heat and energy transfers, such as in heat engines, refrigeration, or climate modeling.

Examples

Example 1: Air in the Atmosphere

The Earth’s atmosphere is a mixture of gases, primarily nitrogen and oxygen, along with trace amounts of other gases like carbon dioxide and argon. The behavior of air as a gas is influenced by factors such as temperature, pressure, and volume. For example, as the temperature increases, the air expands, causing the pressure to decrease if the volume remains constant, illustrating the properties of gases.

Example 2: Diffusion of Perfume

When helium gas is filled into a balloon, it occupies the space inside the balloon and exerts pressure on the walls. Helium is less dense than the surrounding air, allowing the balloon to float. This example demonstrates buoyancy and the principle that gases will rise when they are lighter than the fluid (air) they are in.

Example 3: Temperature and Particle Speed

When a syringe is filled with gas, the gas molecules are in constant motion, colliding with each other and the walls of the syringe. If the plunger is pushed down, the volume of gas decreases, and the pressure inside the syringe increases. This behavior showcases the compressibility of gases and the relationship between pressure and volume, where gases can be easily compressed compared to liquids and solids.

Example 4: Behavior of Gases Under Compression

In a sealed bottle of soda, carbon dioxide gas is dissolved in the liquid under high pressure. When the bottle is opened, the pressure is released, and the gas comes out of solution, forming bubbles. This example illustrates how gases can exist in equilibrium with liquids and how pressure changes can lead to phase transitions, such as gas escaping from a solution.

Example 5: Effusion of Gas Through a Small Hole

When humans exhale, the air released is primarily composed of nitrogen, oxygen, and carbon dioxide. The process of breathing demonstrates the gas phase in a biological context, where the exchange of gases occurs in the lungs. The gas molecules diffuse from areas of higher concentration (in the blood) to lower concentration (in the lungs), exemplifying the principles of gas diffusion and partial pressure.

Practice Questions

Question 1

According to the kinetic molecular theory of gases, which of the following statements is true?

A) Gas particles have strong attractive forces between them.
B) Gas particles are in constant, random motion.
C) Gas particles occupy a fixed volume and shape.
D) Gas particles collide with each other inelastically.

Correct Answer: B) Gas particles are in constant, random motion.

Explanation: The kinetic molecular theory states that gas particles are in constant, random motion and that this motion is what contributes to gas pressure as particles collide with the walls of their container. This is in contrast to option A, which is incorrect because gas particles have negligible attractive forces between them compared to solids and liquids. Option C is also incorrect, as gases do not have a fixed volume or shape; they expand to fill their containers. Option D is incorrect because gas particle collisions are considered elastic, meaning that kinetic energy is conserved during these collisions.

Which of the following factors primarily affects the speed of gas particles according to the kinetic molecular theory?

A) The color of the gas
B) The mass of the gas particles
C) The pressure of the gas
D) The volume of the container

Correct Answer: B) The mass of the gas particles.

Explanation: The speed of gas particles is influenced by their mass; lighter gas particles move faster than heavier particles at the same temperature. This relationship is a key aspect of the kinetic molecular theory, which indicates that temperature is a measure of the average kinetic energy of gas particles. Option A, the color of the gas, has no bearing on particle speed. While pressure and volume can influence the behavior of a gas, they do not directly affect the speed of individual particles in the way that mass does.

Question 3

What happens to the behavior of a gas when the temperature is increased, according to the kinetic molecular theory?

A) The gas particles move slower and come closer together.
B) The gas particles remain at the same speed.
C) The gas particles move faster and collide more frequently with the container walls.
D) The gas particles condense into a liquid.

Correct Answer: C) The gas particles move faster and collide more frequently with the container walls.

Explanation: According to the kinetic molecular theory, increasing the temperature of a gas increases the kinetic energy of the particles, causing them to move faster. As the particles move more quickly, they collide more frequently with the walls of their container, leading to increased pressure if the volume remains constant. Option A is incorrect because increased temperature causes particles to move faster, not slower. Option B is also incorrect, as temperature directly affects particle speed. Option D is incorrect because gases do not condense into liquids under normal temperature increases; condensation occurs when temperature decreases or pressure increases sufficiently.