Titration is a laboratory method used to determine the concentration of an unknown solution by adding a titrant of known concentration until the reaction reaches the equivalence point. Titrations are essential in acid-base chemistry, pharmaceutical applications, and biological systems, particularly in understanding buffer systems and pH regulation.

Free MCAT Practice Test

Learning Objectives

In studying titrations for the MCAT’s Foundation 5: Chemical Processes, you should focus on understanding how titrations determine unknown concentrations, differentiating between acid-base and redox titrations, and recognizing the significance of equivalence and end points. You should also master the use of indicators, analyze titration curves for strong and weak acids or bases, and perform relevant calculations involving molarity and stoichiometry. Lastly, apply titration concepts to biological systems and pharmaceutical contexts, such as understanding buffer systems in blood and drug formulations.

What is Titration?

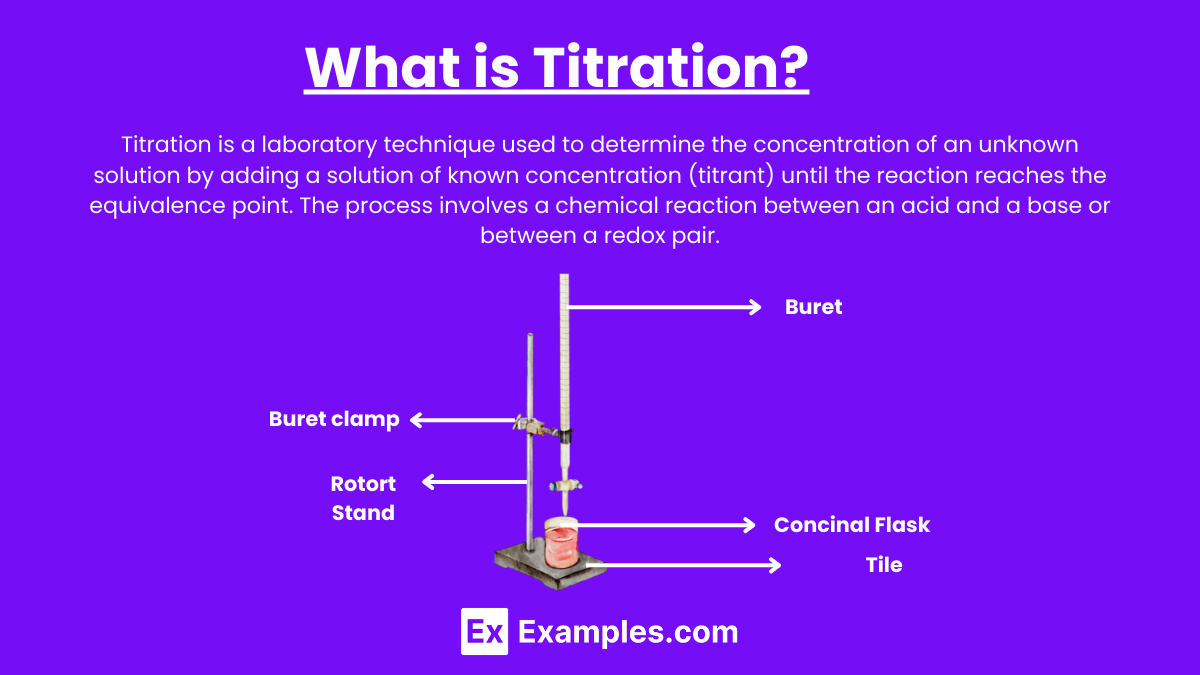
Titration is a laboratory technique used to determine the concentration of an unknown solution by adding a solution of known concentration (titrant) until the reaction reaches the equivalence point. The process involves a chemical reaction between an acid and a base or between a redox pair.

Types of Titrations

Acid-Base Titrations: Involves a reaction between an acid and a base. The titrant can be either an acid or a base, and the goal is to find the concentration of the unknown acid or base.

Example: Using sodium hydroxide (a strong base) to titrate hydrochloric acid (a strong acid).

Redox Titrations: Involves a redox reaction where the oxidation states of atoms change.

Example: Potassium permanganate can be used as a titrant in redox titrations with iron(II) ions.

Equivalence Point and End Point

Equivalence Point: The point at which the amount of titrant added exactly reacts with the amount of substance in the sample. For acid-base titrations, it is the point where moles of H⁺ from the acid equal moles of OH^– from the base.

End Point: The point in a titration where the indicator changes color, signaling that the titration is complete. The end point is ideally close to the equivalence point, but they are not always the same.

Indicators in Acid-Base Titrations

Indicators are substances that change color based on the pH of the solution. They help visually signal the end of the titration. Common indicators include:

Phenolphthalein: Colorless in acidic solutions, turns pink in basic solutions. Used in strong acid/strong base titrations.
Methyl Orange: Red in acidic solutions, yellow in basic solutions. Often used in strong acid/weak base titrations.

Titration Calculations

To perform titration calculations, use the following steps:

Write the balanced chemical equation:
Identify the mole ratio between the titrant and the analyte.
Determine the moles of titrant used:
Use the formula:moles=Molarity (M)×Volume (L)
Use the mole ratio:
Use the stoichiometric relationship from the balanced equation to find the moles of the unknown substance.
Calculate the unknown concentration:
The concentration of the unknown can be calculated by rearranging the formula:
$ \text{Molarity (M)} = \frac{\text{moles}}{\text{Volume (L)}} $

Examples

Example 1: Strong Acid and Strong Base Titration

Titrating hydrochloric acid (HCl) with sodium hydroxide (NaOH) results in complete neutralization, forming water and sodium chloride. The equivalence point occurs at pH 7, where H⁺ from the acid and OH^_ from the base combine to form H₂O.

Example 2: Weak Acid and Strong Base Titration

Titrating acetic acid ($CH_3COOH$) with sodium hydroxide ($NaOH$) results in the formation of water and sodium acetate. The equivalence point occurs at a pH above 7, due to the presence of the conjugate base $CH_3COO^-$.

Example 3: Titration of Ammonia with Hydrochloric Acid

Ammonia ($NH_3$), a weak base, reacts with hydrochloric acid to form ammonium chloride ($NH_4Cl$). The equivalence point occurs below pH 7 because of the formation of the conjugate acid, $NH_4^+$, which slightly lowers the pH.

Example 4: Redox Titration of Iron(II) with Potassium Permanganate

In this redox titration, $Fe^{2+}$ is titrated with potassium permanganate ($KMnO_4$), which oxidizes the iron to $Fe^{3+}$. The color change of permanganate from purple to colorless marks the end point.

Example 5: Buffer Solution Titration

When titrating a buffer solution composed of acetic acid and sodium acetate, the buffer resists significant pH changes until most of the weak acid is neutralized. The titration curve shows a gradual change in pH before the equivalence point is reached.

Practice Questions

Question 1:

During the titration of 50 mL of 0.1 M HCl with 0.1 M NaOH, how much NaOH is required to reach the equivalence point?

A) 10 mL
B) 25 mL
C) 50 mL
D) 100 mL

Answer:
C) 50 mL

Explanation:
At the equivalence point in a strong acid/strong base titration, the moles of $H^+$ and $OH^-$ are equal. Using the formula $M_1V_1 = M_2V_2$, we calculate: $0.1 \, \text{M} \times 50 \, \text{mL} = 0.1 \, \text{M} \times V_2$. Thus, $V_2 = 50 \, \text{mL}$. Therefore, 50 mL of $NaOH$ is required.

Question 2:

Which of the following titrations would result in an equivalence point with a pH greater than 7?

A) $HCl$ titrated with $NaOH$
B) $CH_3COOH$ titrated with $NaOH$
C) $NH_3$ titrated with $HCl$
D) $HNO_3$ titrated with $NaOH$

Answer:
B) $CH_3COOH$ titrated with $NaOH$

Explanation:
In the titration of a weak acid (acetic acid) with a strong base (sodium hydroxide), the equivalence point occurs at a pH greater than 7 due to the presence of the conjugate base (CH3COO^–), which makes the solution slightly basic.

Question 3:

In the titration of 25 mL of 0.1 M acetic acid with 0.1 M sodium hydroxide, what is the pH at the half-equivalence point?

A) pH 2.4
B) pH 4.8
C) pH 7
D) pH 9.2

Answer:
B) pH 4.8

Explanation:

At the half-equivalence point, the concentration of the weak acid equals the concentration of its conjugate base. According to the Henderson-Hasselbalch equation:

$[\text{pH} = \text{pKa} + \log \left( \frac{[\text{A}^-]}{[\text{HA}]} \right)]$
At the half-equivalence point, $[\text{A}^-] = [\text{HA}]$, so $\log(1) = 0$, and:
$[\text{pH} = \text{pKa}]$
For acetic acid, $\text{pKa} = 4.8$, so the pH is 4.8.