Translational motion and calculations are fundamental in physics, describing the movement of objects from one point to another in a straight line. On the MCAT, you’ll explore key concepts such as displacement, velocity, acceleration, and the equations of motion. Understanding Newton’s laws, kinematic equations, and how forces affect motion is crucial, as these principles are essential to mastering the physical sciences section. Additionally, problem-solving skills involving vector components and the relationship between force and energy play a vital role in achieving success in the exam.

Free MCAT Practice Test

Learning Objectives

In studying “Translational Motion and Calculations” for the MCAT, you should learn to analyze motion in a straight line by understanding concepts such as displacement, velocity, acceleration, and time. Develop the ability to apply kinematic equations to solve problems involving constant acceleration. Understand the distinction between average and instantaneous velocity and acceleration. Practice interpreting velocity-time and position-time graphs to determine key motion parameters. Analyze free-fall motion under gravity and identify scenarios involving projectile motion. Evaluate the relationship between force and motion using Newton’s laws to solve translational motion problems. Additionally, master techniques for identifying and calculating net displacement, final velocity, and total distance traveled in complex systems.

Analyzing Motion in a Straight Line

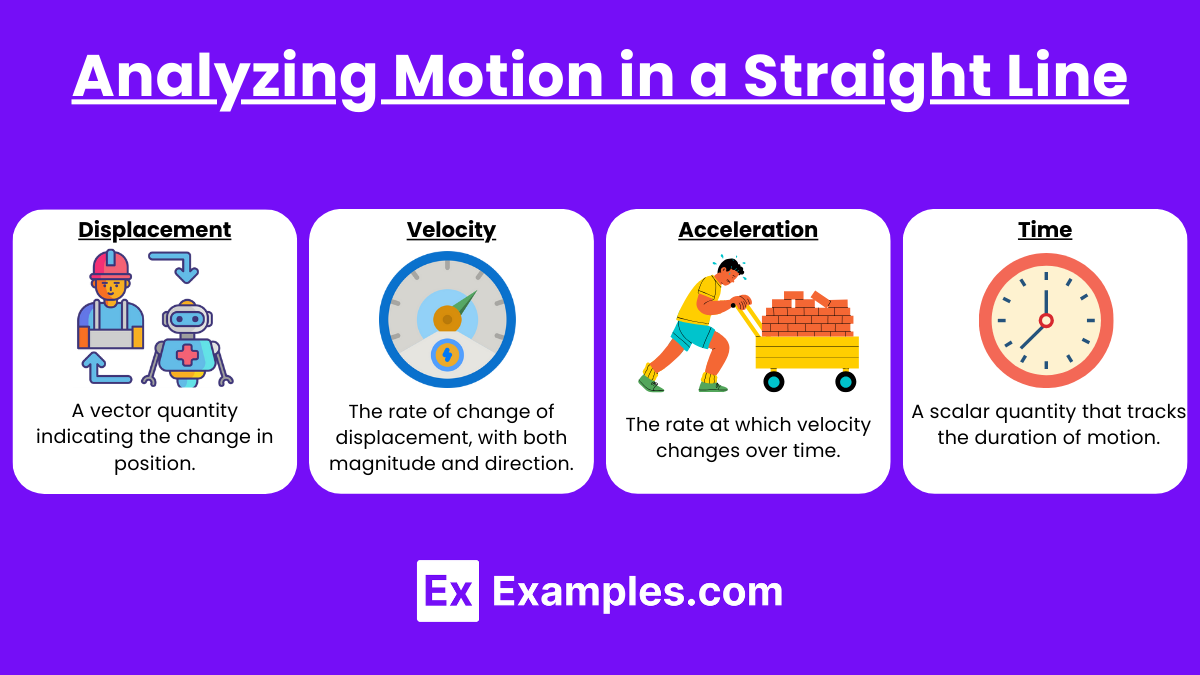
Translational motion describes an object moving in a straight line. Key quantities involved are:

Displacement: A vector quantity indicating the change in position.
Velocity: The rate of change of displacement, with both magnitude and direction.
Acceleration: The rate at which velocity changes over time.
Time: A scalar quantity that tracks the duration of motion.

Example: A car accelerating from rest along a straight path exhibits translational motion where displacement, velocity, and acceleration are interrelated.

Understanding Projectile Motion

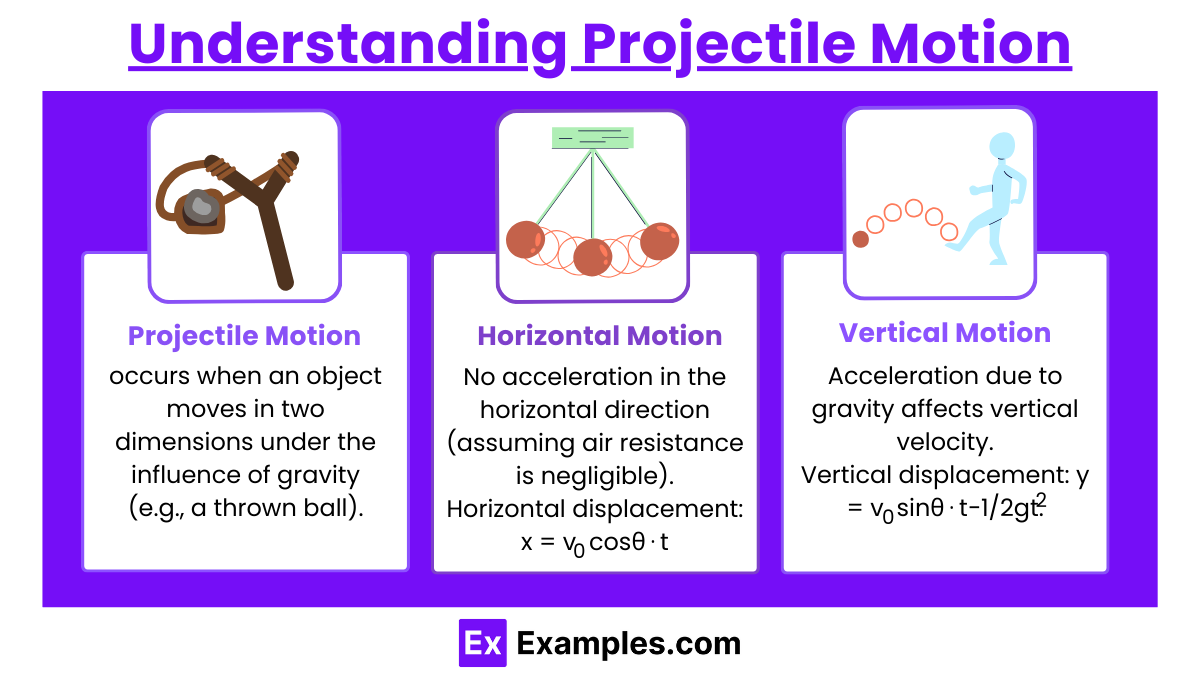
Projectile Motion occurs when an object moves in two dimensions under the influence of gravity (e.g., a thrown ball).
Horizontal Motion: No acceleration in the horizontal direction (assuming air resistance is negligible).
Vertical Motion: Acceleration due to gravity affects vertical velocity.

Key Equations:

Horizontal displacement: x = v₀cos⁡θ⋅t
Vertical displacement: y = v₀sin⁡θ⋅t−1/2gt².

Evaluating Force and Motion Using Newton’s Laws

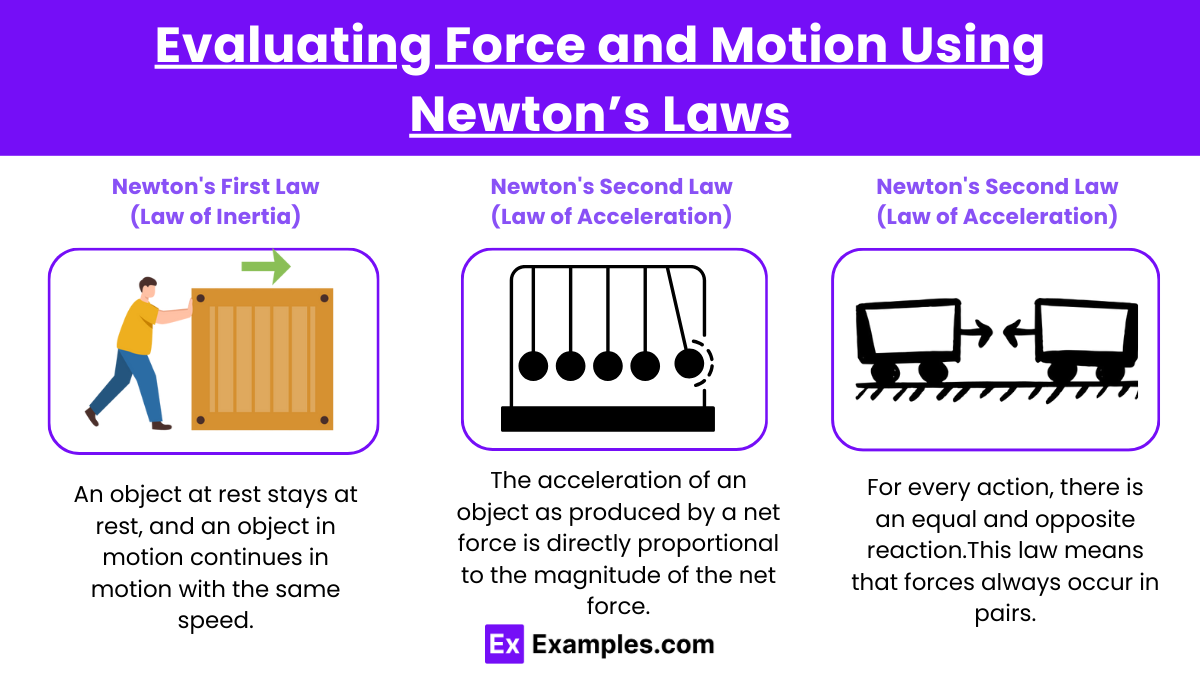
Newton’s First Law (Law of Inertia)

An object at rest stays at rest, and an object in motion continues in motion with the same speed and in the same direction unless acted upon by an unbalanced force.

This law explains the behavior of objects in terms of changes to their state of motion. For instance, if a car suddenly stops, the passengers inside continue to move forward due to inertia. It emphasizes the need for a force to change the motion of an object.

Newton’s Second Law (Law of Acceleration)

The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.

This law provides the formula for calculating the force on an object: F = ma where is the net force applied to the object, m is the mass of the object, and is the acceleration. For example, pushing a shopping cart with a certain force results in acceleration proportional to that force and inversely proportional to the mass of the cart and its contents.

Newton’s Third Law (Law of Action and Reaction)

For every action, there is an equal and opposite reaction.

This law means that forces always occur in pairs. If object A exerts a force on object B, object B simultaneously exerts a force of equal magnitude and opposite direction on object A. This principle is evident in a variety of situations, from the kickback of a gun when fired to the force a swimmer must apply to push against the water to move forward.

Evaluating Problems Using Newton’s Laws

To apply Newton’s laws to solve problems in mechanics, follow these steps:

Identify the System: Determine which object(s) you are analyzing.
Draw a Free-Body Diagram: Sketch the object and all forces acting upon it, labeling each force with its type and direction.
Apply Newton’s Second Law: Set up equations based on F = ma to find unknown quantities. This often involves resolving forces into their components.
Solve the Equations: Use algebra to solve for the unknowns, such as acceleration or individual forces.
Check Results: Ensure the solution makes sense physically (e.g., checking the direction of acceleration and the balance of forces).

Mastering Techniques for Net Displacement, Final Velocity, and Total Distance Traveled

Average velocity: Average velocity is defined as the total displacement divided by the total time taken to cover that displacement. It is a vector quantity, which means it has both magnitude and direction.
Instantaneous Velocity: Instantaneous velocity is the velocity of an object at a specific moment in time. It provides a more detailed description of the object’s motion and is effectively the derivative of position with respect to time.
Average Acceleration: Average acceleration is defined as the change in velocity divided by the time over which the change occurs. It is a vector quantity.
Instantaneous Acceleration: Instantaneous acceleration is the acceleration of an object at a specific instant in time. It is the derivative of velocity with respect to time and can be understood as the second derivative of position.

Examples

Example 1: Free Fall

A stone dropped from a height of 20 meters experiences gravitational acceleration, resulting in a specific time to reach the ground. By calculating this time, we can understand how quickly the stone falls and impacts the ground.

Example 2: Horizontal Projectile Motion

When a ball is kicked off a table that is 1.5 meters high, it travels horizontally while falling. By observing the time taken to hit the ground and the horizontal distance it covers, we can determine the ball’s speed and trajectory as it descends.

Example 3: Inclined Plane

A block sliding down a frictionless incline at a 30-degree angle accelerates due to gravity. By measuring the distance traveled along the incline, we can estimate how fast the block moves when it reaches the bottom, showcasing the effects of gravitational force on motion.

Example 4: Uniform Circular Motion

A car driving around a circular track with a radius of 50 meters at a steady speed experiences a constant inward acceleration. By analyzing the speed and path of the car, we can understand how the car maintains its circular motion and the forces acting upon it.

Example 5: Linear Motion with Constant Acceleration

A car accelerating from a complete stop at a steady rate travels a distance of 100 meters. By tracking the time taken to cover this distance, we can gain insight into how acceleration affects the car’s speed over time and its overall motion.

Practice Questions

A ball is dropped from a height of 45 meters. Which of the following statements is true about its motion just before it hits the ground?

A) The ball moves at a constant speed throughout its fall.
B) The ball accelerates downward due to gravity.
C) The ball’s motion is unaffected by air resistance.
D) The ball’s potential energy decreases but its kinetic energy remains constant.

Correct Answer: B) The ball accelerates downward due to gravity.

Explanation: When an object is in free fall, it accelerates downward because of the force of gravity acting on it. This means that the speed of the ball increases as it falls. While air resistance does have some effect, it is generally negligible for a small ball falling a short distance. Thus, option B is correct, as the ball’s acceleration is directed downwards due to gravity.

Question 2:

A car is moving in a straight line at a constant speed of 60 km/h. Which of the following describes the translational motion of the car?

A) The car is accelerating.
B) The car is in uniform motion.
C) The car is decelerating.
D) The car is changing direction.

Correct Answer: B) The car is in uniform motion.

Explanation: When an object moves at a constant speed in a straight line, it is said to be in uniform motion. This means that its speed does not change, and it is not accelerating or decelerating. Option A is incorrect because the car is not speeding up; option C is also incorrect because it is not slowing down. While option D could be true if the car were to turn, it is not applicable since the question specifies straight-line motion.

Question 3:

A runner completes a 400-meter lap around a track in 50 seconds. What can be concluded about the runner’s average speed during this lap?

A) The average speed is 8 m/s.
B) The average speed varies throughout the lap.
C) The runner’s speed at the halfway point is greater than the average speed.
D) The runner’s speed cannot be determined without more information.

Correct Answer: A) The average speed is 8 m/s.

Explanation: Average speed is calculated by dividing the total distance traveled by the total time taken. In this case, the runner travels 400 meters in 50 seconds. Therefore, the average speed is determined to be 8 meters per second. Option B is incorrect because the average speed is a specific value and does not account for variations during the lap. Option C is misleading as it does not necessarily mean the speed at the halfway point is greater than the average speed. Lastly, option D is incorrect because the average speed can indeed be calculated with the given information.