Vector analysis and forces acting on an object

Vector analysis and forces acting on an object are essential concepts in physics, focusing on how different forces influence motion and equilibrium. On the MCAT, you’ll explore vector components, vector addition, and the use of free-body diagrams to analyze force systems. Understanding Newton’s laws, frictional forces, tension, and torque is crucial, as these principles are fundamental to mastering mechanics and kinematics sections of the exam.AP United States History Practice test 14AP United States History Practice test 14

Learning Objectives

In studying “Vector Analysis and Forces Acting on an Object” for the MCAT, you should learn to analyze and resolve vectors into their components to understand how forces interact in multiple dimensions. Understand how to apply Newton’s laws using vector principles to determine the net force on an object. Practice calculating resultant forces through vector addition and subtraction, using both graphical methods and algebraic techniques. Learn to identify equilibrium conditions when the net force is zero and solve problems involving objects at rest or in uniform motion. Analyze free-body diagrams to break forces into vertical and horizontal components and apply trigonometry to solve for unknowns. Additionally, develop proficiency in understanding how friction, tension, normal force, and gravity contribute to the overall force system in real-world MCAT scenarios.

Analyzing and Resolving Vectors into Their Components

Understanding Vectors

A vector is a quantity that has both magnitude and direction. Common examples include displacement, velocity, acceleration, and force.

Why Resolve Vectors?

Resolving vectors into components helps to:

• Simplify calculations by transforming vector quantities into simpler scalar quantities along perpendicular axes (typically x and y axes).
• Allow the use of algebraic methods to add, subtract, and multiply vectors, which is particularly useful in solving physics problems.

Steps to Resolve a Vector into Components

To resolve a vector into its components along orthogonal (perpendicular) axes, typically horizontal (x-axis) and vertical (y-axis), follow these steps:

• Choose a Coordinate System: Orient your coordinate system to simplify calculations, typically aligning axes with the motion or forces.
• Draw the Vector: Accurately draw the vector from a specific origin point. Ensure the length and direction accurately represent the vector’s magnitude and direction.
• Determine the Angle: Identify the angle the vector makes with your reference line (usually the horizontal x-axis).

Use Trigonometric Functions to Find Components:

• Horizontal Component (x-component): Use the cosine function. V_x = Vcos⁡(θ)
• Vertical Component (y-component): Use the sine function. V_y = Vsin⁡(θ)

Here, V is the magnitude of the vector, and θ\thetaθ is the angle it makes with the horizontal axis.

Applying Newton’s Laws Using Vector Principles

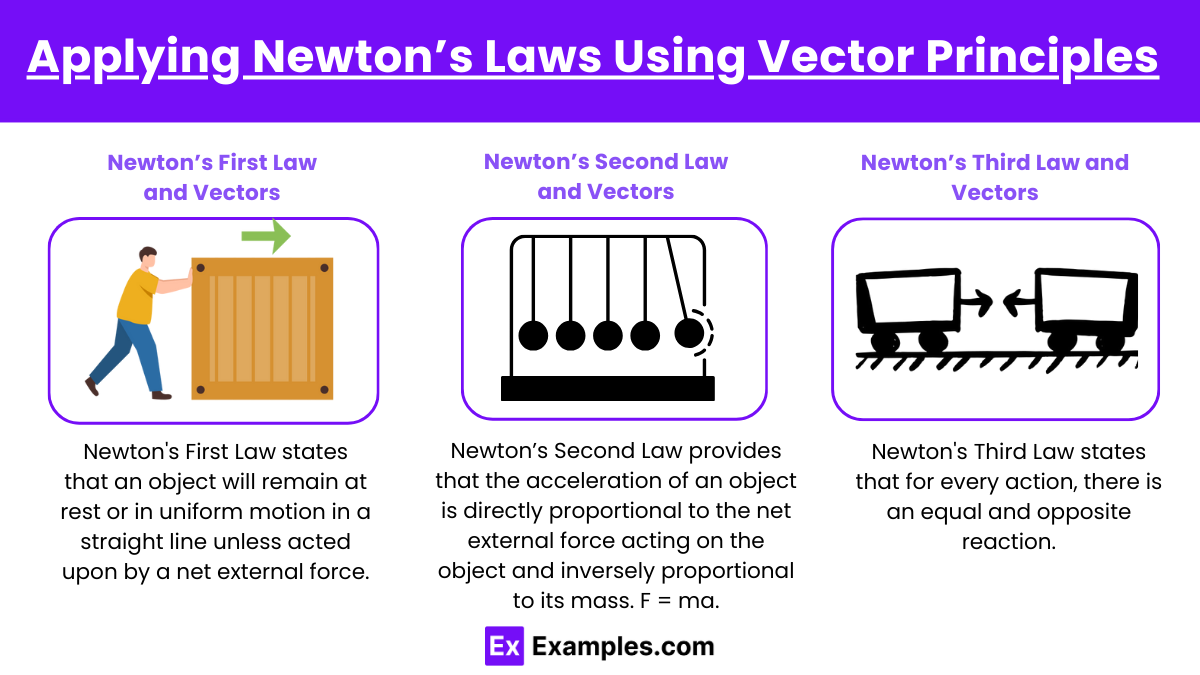
Newton’s First Law and Vectors

Newton’s First Law states that an object will remain at rest or in uniform motion in a straight line unless acted upon by a net external force. Using vector principles, this law implies that if the vector sum of all forces acting on an object (known as the net force) is zero, the object’s velocity (a vector quantity) remains constant. This concept is foundational in statics, where structures must be designed to ensure that all forces balance to maintain stability.

Newton’s Second Law and Vectors

Newton’s Second Law provides that the acceleration of an object is directly proportional to the net external force acting on the object and inversely proportional to its mass. In vector terms, this law is expressed as F = ma, where F (force) and a (acceleration) are vectors. This law is crucial for dynamics:

• The direction of the acceleration vector is the same as the direction of the net force vector.
• The magnitude of the acceleration can be influenced by the magnitude of the force and the mass of the object.

This law allows engineers and physicists to predict the motion of an object by considering all the vector forces acting upon it, such as gravitational force, friction, tension, and normal forces.

Newton’s Third Law and Vectors

Newton’s Third Law states that for every action, there is an equal and opposite reaction. In vector terms, this means that if an object A exerts a force on object B, then object B simultaneously exerts a force of equal magnitude but in the opposite direction on object A. These force vectors are crucial in analyzing interactions like collisions or when objects push against each other.

Applying Vector Principles

Using vectors allows for a more nuanced understanding and application of these laws:

• Vector Addition: When multiple forces act on an object, they must be added vectorially to find the resultant or net force. This involves adding their magnitudes in their respective directions, which can be done graphically or by breaking each force into its components.
• Resolution of Forces: Often, forces are not aligned along the same line and must be resolved into perpendicular components (usually horizontal and vertical). This simplifies the application of Newton’s laws, as each component can be treated independently.
• Equilibrium Conditions: Using vector principles, the conditions for equilibrium (static or dynamic) involve setting the sum of the force vectors in each direction to zero, ensuring no net force and hence no acceleration.

Understanding the Contribution of Friction, Tension, Normal Force, and Gravity

Gravity

Gravity is a fundamental force that acts between all masses in the universe. On Earth, it gives weight to physical objects and causes them to fall toward the ground when dropped. The force of gravity:

• Acts vertically downward toward the center of the Earth.
• Affects every object with mass, influencing everything from the trajectory of a ball to the orbits of planets.

Normal Force

The normal force is a reactive force that surfaces exert to support objects resting on them. It prevents objects from “falling” into whatever they are resting on by pushing back with a force equal and opposite to the component of the gravitational force perpendicular to the surface. Key characteristics include:

• Acting perpendicular to the contact surface between objects.
• Balancing the vertical component of gravity when an object is resting on a horizontal surface.
• Changing based on the angle of the surface, which affects how the components of gravity are balanced.

Friction

Friction is the force that opposes the relative motion or the attempt at motion between two surfaces in contact. It is crucial for many everyday activities, such as walking and driving, as it provides the necessary grip. Frictional force:

• Acts parallel to the surface of contact.
• Opposes the direction of motion or potential motion.
• Varies depending on the nature of the surfaces in contact and the normal force exerted between them.
• Can be static (preventing motion from starting) or kinetic (opposing ongoing motion).

Tension

Tension is the pulling force transmitted along the length of a flexible connector, such as a rope, cable, string, or chain, when it is pulled tight by forces acting from opposite ends. Tension:

• Is evenly distributed along the length of the wire or rope (assuming the rope is massless and the tension is constant).
• Acts along the line of the rope or wire and pulls equally on the objects attached to both ends.
• Is essential in systems involving pulleys, bridges, and elevators, providing the necessary force to support structures or move objects.

Examples

Example 1: Tension in a Rope

When two people pull on a rope in opposite directions, the tension in the rope can be analyzed as a vector. Each person’s pull generates a force that can be broken down into its components. For example, if one person pulls with a force of 50 N at an angle of 30 degrees from the horizontal, vector analysis allows us to determine the horizontal and vertical components of the force. This analysis helps in understanding how the forces interact and whether the rope will remain taut or if one person will be able to pull the other closer.

Example 2: Projectile Motion

When a ball is thrown at an angle, its motion can be analyzed using vector components. The initial velocity can be split into horizontal and vertical components, which are analyzed separately. Gravity acts downward on the ball, providing a vertical force that affects its trajectory. By applying vector analysis, we can predict the ball’s path, maximum height, and the distance it will travel before hitting the ground.

Example 3: Equilibrium of Forces

In a scenario where an object, such as a lamp, is suspended by two strings at different angles, vector analysis is crucial. Each string exerts a tension force that can be resolved into components. For the lamp to remain in equilibrium, the sum of the forces in both the horizontal and vertical directions must be zero. By analyzing the vectors, one can determine the tensions in the strings and ensure that the lamp does not move.

Example 4: Inclined Plane

When an object is placed on an inclined plane, the forces acting on it can be analyzed using vector components. The gravitational force acting on the object can be resolved into two components: one parallel to the incline and one perpendicular to it. The parallel component causes the object to slide down, while the perpendicular component is balanced by the normal force. Vector analysis helps in calculating the net force acting on the object and predicting its acceleration down the slope.

Example 5: Frictional Forces

When a box is pushed across a surface, friction opposes its motion. The applied force can be represented as a vector, and the frictional force can also be expressed as a vector acting in the opposite direction. By analyzing these forces, one can determine if the applied force is sufficient to overcome friction and initiate motion. If the applied force is greater than the frictional force, the box will move; otherwise, it will remain stationary. This vector analysis is essential for understanding the dynamics of motion.

Practice Questions

Question 1

A box is pushed across a floor with a force of 10 N to the right and a frictional force of 4 N acting to the left. What is the net force acting on the box?

A) 6 N to the right
B) 4 N to the left
C) 10 N to the right
D) 14 N to the right

Correct Answer: A) 6 N to the right.

Explanation: The net force is determined by combining all the forces acting on an object. In this case, the applied force of 10 N to the right and the opposing frictional force of 4 N to the left result in a net force of 6 N to the right. This shows how vector addition works in determining the overall force acting on an object.

Question 2

An object at rest on a table remains stationary despite the gravitational force acting on it. Which of the following best explains this phenomenon?

A) The object has no weight.
B) The gravitational force is balanced by an equal force from the table.
C) The object is experiencing acceleration.
D) The forces are unbalanced, causing motion.

Correct Answer: B) The gravitational force is balanced by an equal force from the table.

Explanation: According to Newton’s first law, an object at rest will remain at rest unless acted upon by an unbalanced force. In this case, the downward gravitational force is counteracted by the upward normal force exerted by the table. These two forces are equal in magnitude and opposite in direction, resulting in no net force and keeping the object stationary.

Question 3

A person is pulling a wagon with a force directed at an angle of 30 degrees above the horizontal. Which of the following statements is true regarding the forces acting on the wagon?

A) The vertical component of the pull increases the normal force.
B) The horizontal component of the pull is irrelevant.
C) The wagon will not move because the pull is at an angle.
D) The pull does not affect the weight of the wagon.

Correct Answer: A) The vertical component of the pull increases the normal force.

Explanation: When the person pulls the wagon at an angle, the force can be divided into two components: horizontal and vertical. The vertical component acts upward, countering some of the gravitational force acting on the wagon. This effectively increases the normal force because the table or ground must support not only the weight of the wagon but also the additional upward force from the pull. Therefore, the net effect of the pull results in a greater normal force acting on the wagon.