What does Ampere's Law relate?
Electric field and charge distribution
Magnetic field and electric current
Gravitational field and mass
Magnetic field and voltage
of 10
Amperes Law – Examples, Definition, Uses, FAQ’S
Amperes Law – Examples, Definition, Uses, FAQ’S
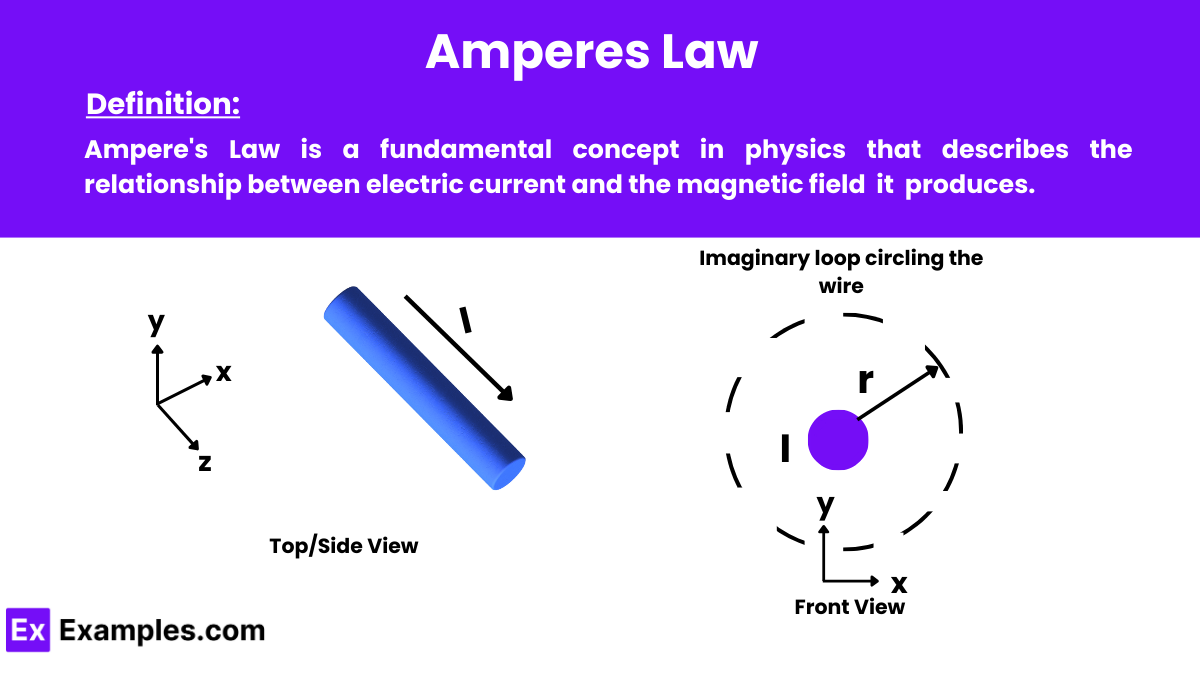
Ampere’s Law is a fundamental concept in physics that describes the relationship between electric current and the magnetic field it produces. Part of the broader laws of physics known as Maxwells equations, Amperes Law states that the integral of the magnetic field around a closed loop is proportional to the total current passing through the loop.
What is Amperes Law?
Who Was Andre-Marie Ampere?
André-Marie Ampère (1775-1836) was a French physicist and mathematician who is widely recognized as one of the founders of electromagnetism. His pioneering work laid the groundwork for the field of electrodynamics, which studies the interaction between electric currents and magnetic fields.
What Is Ampere’s Circuital Law?
Ampère’s Circuital Law can be express as the line integral of the magnetic field around a closed loop being directly proportional to the total current passing through the loop.
If a conductor carries a current 𝐼, this flow of current generates a surrounding magnetic field.
The equation left side shows that the sum of the magnetic field along an imaginary path that encircle the conductor will numerical equal the current passing through that loop, denoted as 𝐼ₑₙ꜀
Amperes Law Formula
The formula for Ampere’s Law relates the magnetic field to the electric current passing through a closed loop:
- where:
- 𝐵: Magnetic field vector,
- 𝑑𝑙: Infinitesimal element of the closed loop,
- 𝜇₀: Permeability of free space (a constant, approximately 4𝜋×10⁻⁷ T m/A),
- 𝐼ₑₙ꜀: Total current passing through the loop.
This integral equation means that the line integral of the magnetic field around a closed path is proportional to the sum of the current passing through the enclosed area.
Determining Magnetic Field by Ampere’s Law
To find the magnetic field around a long, current-carrying wire at any distance 𝑟, apply Ampère’s Law using an imaginary loop surrounding the wire, as shown below:
Step-by-Step Process:
Define an Amperian Loop: Encircle the wire with a circular loop (shown in blue) at a distance 𝑟 from the wire, forming a path of circumference 2𝜋𝑟.
Apply Symmetry: By symmetry, the magnetic field remains constant in magnitude along the loop, simplify the integral calculation.
Use Ampère’s Law: Apply Ampère’s Law: ∮𝐻⋅𝑑𝐿=2𝜋𝑟𝐻=𝐼ₑₙ꜀
where:
- 𝐻 is the magnitude of the magnetic field,
- 𝐼ₑₙ꜀ is the current enclosed by the loop,
- 𝑑𝐿 is an infinitesimal segment of the loop.
Solve for the Magnetic Field:
𝐻=𝐼ₑₙ꜀/2𝜋𝑟
The equation shows that the magnetic field decreases in magnitude as you move farther from the wire. According to the inverse relationship with distance 𝑟.
The field’s direction is tangential to the loop at every point and can be determined using the right-hand rule: if you point your thumb in the direction of the current, your fingers curl in the direction of the magnetic field.
Uses of Amperes Law
- Electromagnets: Helps in designing electromagnet by determine how much magnetic field will be generate for a given current.
- Coils and Solenoids: Calculates the magnet field inside coils and solenoids, essential for electric motors, transformers, and relays.
- Magnetic Sensors: Helps create magnet field sensors like Hall-effect devices, which detect the presence and strength of magnet fields.
- Circuit Design: Assists in understanding how current create magnetic fields, aiding in circuit and PCB design to minimize interfere.
- Physics Research: Supports scientific research in electromagnetism by explain how current and magnetic fields interact.
- MRI Machines: Guides the design of MRI machines, ensure strong, uniform magnetic fields for accurate medical imaging.
Examples for Amperes Law
- Long Straight Wire: A current passing through a long, straight wire creates concentric circles of magnetic fields around the wire.
- Using Ampère’s Law, one can calculate the magnetic field strength at various distances from the wire.
- Solenoid: A solenoid, a coil of wire, produce a uniform magnetic field inside it when current flows through it.
- Toroid: A toroid, a coil wound in a circle loop, forms a continuous path for the magnetic field.
- Ampère’s Law allows the calculation of the magnetic field inside the toroid based on the current, the number of turns, and the distance from the center.
- Circular Loop: For a circular current-carrying loop, Ampère’s Law provides a way to find the magnetic field at the loop’s center by using the current and loop radius.
- Electromagnets: Electromagnets are coils of wire that generate a magnetic field when electricity flows through them.
FAQ’S
What is Ampère’s Law?
Ampère’s Law relates a magnetic field around a closed loop to the current passing through the loop. It forms a key part of Maxwell’s equations, describe electromagnetism.
How does Ampère’s Law help determine magnetic fields?
It calculates the magnetic field strength and direction created by a current, by considering the integral of the magnetic field around a chosen path.
What is an Amperian loop?
An Amperian loop is an imaginary, closed path around a current-carrying conductor used to calculate the magnetic field via Ampère’s Law.
How does symmetry play a role in applying Ampère’s Law?
Symmetry simple the integral of the magnetic field around an Amperian loop, making it easier to calculate the magnetic field strength in symmetric configuration.
How does Ampère’s Law apply to solenoids?
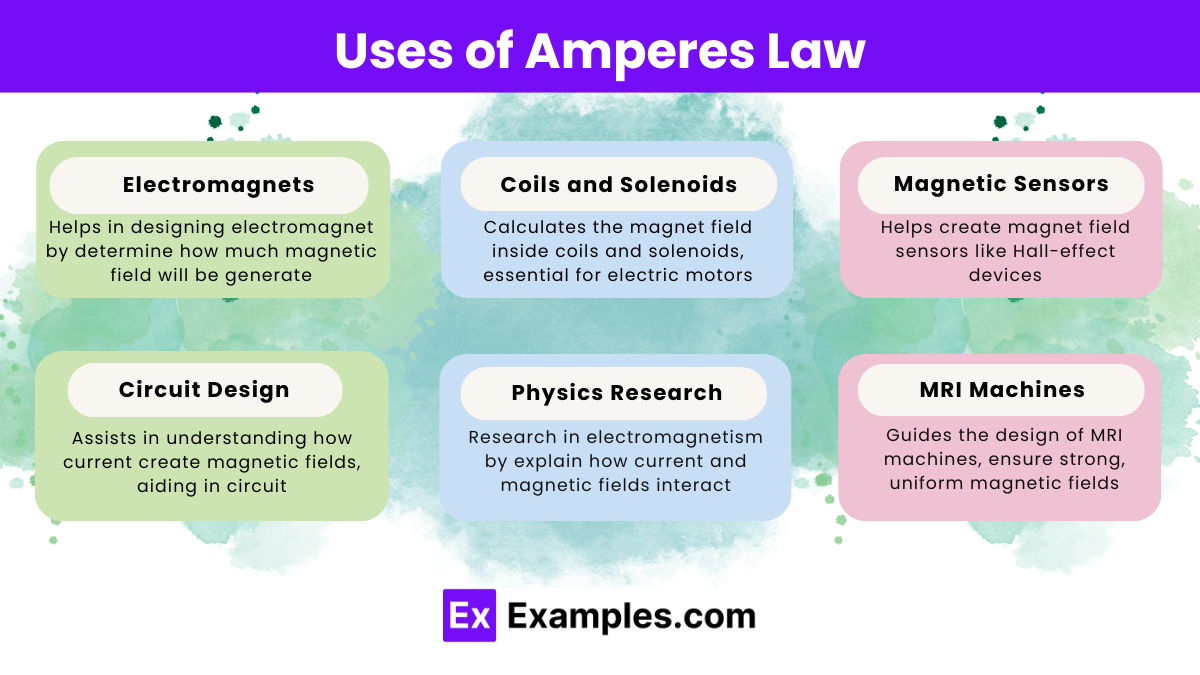
In solenoids, the law helps calculate the magnetic field inside the coil, which depends on the number of wire turns and the current.
What is the relationship between current and the magnetic field?
Ampère’s Law shows that an increase in current directly strengthens the magnetic field around a conductor.
How does Ampère’s Law relate to electromagnets?
The law helps design electromagnet by calculate the magnetic field generate based on current, coil turns, and geometry.
What role does permeability play in Ampère’s Law?
Permeability measures a material ability to support a magnetic field, affecting the strength of the field calculate through Ampère’s Law.
What’s the difference between Ampère’s Law and Gauss’s Law?
Ampère’s Law deals with magnet fields and current, while Gauss’s Law relates electric fields to electric charges.
What are the practical uses of Ampère’s Law?
It is used in designing solenoids, transformers, electromagnets, and magnetic field shield for scientific research and practical applications like MRI machines.
Share :
Practice Test
What is the integral form of Ampere's Law?
∮B·dl = μ₀I
∮E·dl = q/ε₀
∮B·dl = q/ε₀
∮E·dl = μ₀I
of 10
What does μ₀ represent in Ampere's Law?
Electric constant
Gravitational constant
Magnetic permeability of free space
Coulomb constant
of 10
How does Ampere's Law apply to a solenoid?
It shows the electric field inside the solenoid.
It shows the magnetic field inside the solenoid.
It shows the voltage across the solenoid.
It shows the charge distribution within the solenoid.
of 10
What is the magnetic field inside an ideal solenoid according to Ampere's Law?
B = μ₀nI
B = μ₀I/2πr
B = qvB
B = μ₀I/4πr²
of 10
Which law is a special case of Ampere's Law with Maxwell's correction?
Gauss's Law
Faraday's Law
Biot-Savart Law
Ampere-Maxwell Law
of 10
What does Ampere's Law state in the absence of a magnetic field?
The electric field is zero.
The current is zero.
The magnetic flux is constant.
The voltage is constant.
of 10
What is the relationship between the magnetic field B and the distance r from a long straight conductor according to Ampere's Law?
B ∝ r
B ∝ 1/r
B ∝ r²
B ∝ 1/r²
of 10
Which of the following is an application of Ampere's Law?
Calculating the electric field around a point charge
Determining the magnetic field inside a toroid
Finding the potential difference across a capacitor
Measuring the resistance of a wire
of 10
How is Ampere's Law used to derive the magnetic field inside a coaxial cable?
By integrating the electric field over the surface area
By measuring the current density in the cable
By calculating the voltage drop along the cable
By applying the law to a circular path inside the cable
of 10