Biot Savart Law Derivation

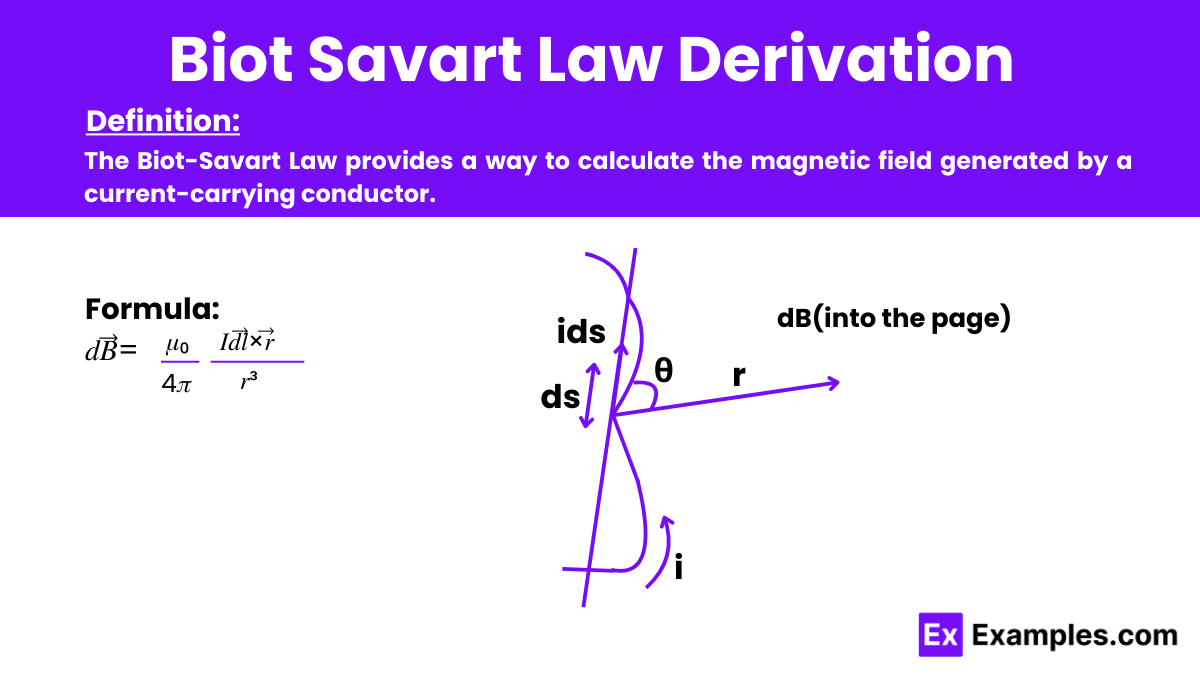
The Biot-Savart Law provides a way to calculate the magnetic field generated by a current-carrying conductor. It states that the infinitesimal magnetic field (𝑑𝐵⃗) at a point in space due to a small segment of current (𝐼) is:

where:

• 𝑑𝑙⃗ is the infinitesimal length vector of the current element.
• 𝑟⃗ is the position vector from the current element to the point where 𝑑𝐵⃗.
• 𝑟 is the magnitude of 𝑟⃗.
• 𝜇 is the permeability of free space.

Derivation

Consider a Current Element:

Assume a small current element 𝑑𝑙⃗ carrying a current 𝐼.

Apply the Concept of Magnetic Field:

The magnetic field due to this current element at a point 𝑃 at a distance r is perpendicular to both the direction of the current and the line connecting the current element to the point 𝑃.

Calculate the Magnetic Field:

The infinitesimal magnetic field is calculated by considering the contribution of the small current element using experimental observations and the cross product.

Formulate the Biot-Savart Law:

By experimental measurements, it was found that 𝑑𝐵⃗ is proportional to the current, 𝑑𝑙⃗, and sin⁡𝜃 (where 𝜃θ is the angle between 𝑑𝑙⃗ and 𝑟⃗), and inversely proportional to 𝑟².

These findings form the basis of the Biot-Savart Law: 𝑑𝐵⃗=𝜇₀/4𝜋𝐼 𝑑𝑙⃗×𝑟⃗/𝑟³​

Example

Let’s consider an example of the Biot-Savart law to calculate the magnetic field at the center of a circular current-carrying loop.

Magnetic Field at the Center of a Current-Carrying Loop

Given: A circular loop with radius 𝑅 carrying a current 𝐼.

Find: The magnetic field at the center of the loop.

Solution:

Place the loop in the xy-plane with its center at the origin.

The current flows in a circular path in the counterclockwise direction.

For an infinitesimal current element 𝑑𝑙⃗ on the loop, the position vector to the center of the loop is 𝑟⃗, and 𝑟=𝑅.

Since 𝑑𝑙⃗ is tangential to the loop, 𝑟⃗ is perpendicular to 𝑑𝑙⃗.

The Biot-Savart Law for this current element becomes: 𝑑𝐵⃗=𝜇₀/4𝜋𝐼 𝑑𝑙⃗×𝑟⃗/𝑟3=𝜇₀/4𝜋𝐼 𝑑𝑙⃗/𝑅²​

The cross product of 𝑑𝑙⃗ and 𝑟⃗ simplifies because they are perpendicular, and the magnitude becomes 𝑑𝑙⃗⋅1.

Since the magnetic field components due to each element 𝑑𝑙⃗ are in the same direction (perpendicular to the loop plane), they add up constructively.

Integrating around the entire loop, the total magnetic field becomes: 𝐵=𝜇₀𝐼/4𝜋𝑅²⋅2𝜋𝑅=𝜇₀𝐼/2𝑅​

The factor 2𝜋 accounts for the total circumference of the loop.

The magnetic field at the center of a circular loop carrying current 𝐼 with radius 𝑅 is 𝐵=𝜇₀𝐼/2R. This example shows how the Biot-Savart Law can be applied to find the magnetic field created by specific current distributions.

Problem:

Find the magnetic field at the center of a square current-carrying loop with side length 𝑎 and current 𝐼.

Solution:

The square loop lies in the xy-plane, centered at the origin.

Each side of the square contributes to the magnetic field at the center.

Applying Biot-Savart Law to One Side:

Consider one side of the loop parallel to the x-axis from −𝑎/2 to 𝑎/2.

The distance from each point on the side to the center is √(𝑎/2)²+(𝑎/2)²=𝑎/√2​.

The magnetic field due to a segment 𝑑𝑥 is: 𝑑𝐵=𝜇₀𝐼/4𝜋𝑑𝑥/(𝑎/√2)²​

Summing Contributions from All Sides:

The total magnetic field is the vector sum of the contributions from all four sides.

The result is: 𝐵=2√2𝜇₀𝐼/𝜋𝑎​.

Practice Problems and Solutions

Problem 1:

Calculate the magnetic field at a point on the axis of a circular loop of radius 𝑅, carrying a current 𝐼, at a distance 𝑥 from the center of the loop.

Solution:

Using Biot-Savart Law:

The magnetic field at a point on the axis is given by: 𝑑𝐵⃗=𝜇₀/4𝜋𝐼 𝑑𝑙⃗×𝑟⃗/𝑟³​

𝑑𝑙⃗ is the small length element, and 𝑟⃗ is the distance from the element to the point on the axis.

Symmetry Considerations:

The tangential components cancel each other due to symmetry, and only the components along the axis contribute.

The total magnetic field along the axis (𝐵𝑥​) is given by: 𝐵𝑥=𝜇₀𝐼𝑅²/2(𝑅²+𝑥²)^3/2

Problem 2:

A straight conductor of length 𝐿 carries a current 𝐼. Find the magnetic field at a point 𝑃 perpendicular to the conductor, at a distance 𝑎 from its midpoint.

Solution:

Setup and Considerations:

Let the conductor lie along the x-axis from −𝐿/2 to 𝐿/2.

Let the point 𝑃 be along the y-axis at a distance 𝑎 from the x-axis.

Applying the Biot-Savart Law:

The infinitesimal magnetic field due to an element 𝑑𝑥 at a distance

𝑟=√𝑥²+𝑎²​ is: 𝑑𝐵=𝜇₀𝐼𝑑𝑥/4𝜋𝑟²

The angle between 𝑑𝑙⃗and 𝑟⃗ is 90⁰, making the cross product 𝑑𝑙⃗×𝑟⃗=𝑑𝑥.

Integrating to Find the Total Field:

Integrating from −𝐿/2 to 𝐿/2, and considering only the perpendicular component: 𝐵=𝜇₀𝐼𝑎/4𝜋∫−𝐿/2𝐿/2𝑑𝑥(𝑥²+𝑎²)^3/2​

The integral yields: 𝐵=𝜇₀𝐼/2𝜋𝑎(𝐿/√𝐿²+4𝑎²)

Problem 3:

Find the magnetic field at the center of a square loop of side length 𝑎, carrying current 𝐼.

Solution:

Analyzing the Problem:

The square loop can be divided into four equal sides.

By symmetry, each side contributes equally to the magnetic field at the center.

Applying the Biot-Savart Law:

Each side contributes a magnetic field perpendicular to the plane of the loop.

For each side, the magnetic field at the center is calculated using the Biot-Savart law:

𝑑𝐵=𝜇₀𝐼/4𝜋∫−𝑎/2𝑎/2𝑑𝑥/(𝑎/2)²

Combining Results:

After summing the contributions of all four sides: 𝐵=2√2𝜇₀𝐼/𝜋𝑎​