What is the formula for Bragg's Law?
nλ = 2d sinθ
nλ = d/2 sinθ
λ = 2nd sinθ
nλ = 2d cosθ
of 10
Braggs Law – Examples, Formulas, differences, FAQs
Braggs Law
Braggs Law Formula
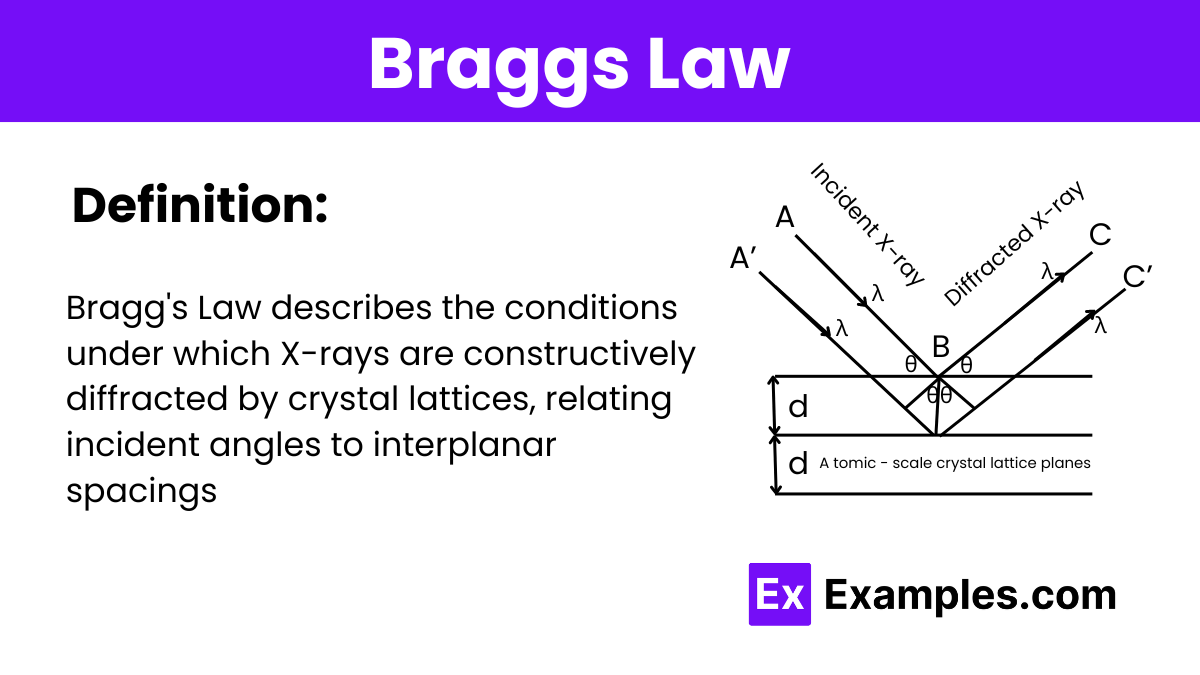
Where:
n is the order of the diffracted beam, which is an integer (1, 2, 3, …),
λ is the wavelength of the incident X-ray,
d is the distance between the crystal planes in the lattice,
θ is the angle of incidence at which the X-rays strike the crystal planes.
Derivation of Bragg’s Law
Step-by-Step Derivation
X-ray Incident and Reflection:
Consider an X-ray beam hitting a set of crystal planes at an angleθ (the incident angle relative to the plane). The X-ray is then reflected off the planes at the same angleθ due to the law of reflection.
Path Difference Calculation:
Focus on two adjacent planes in the crystal. When an X-ray photon hits the first plane, part of the beam is reflected, and part penetrates deeper and is reflected off the second plane.
The extra path traveled by the ray that penetrates to the second plane and then reflects back to the point of initial reflection involves traveling down to the second plane and back up. This extra path length is crucial for understanding the conditions for constructive interference.
Geometry of the Path Difference:
The path difference between the ray that reflects off the first plane and the ray that reflects off the second plane is2dsinθ. Here,d is the distance between the planes (interplanar spacing), andθ is the angle of incidence/reflection.
The factor of 2 comes from the ray traveling down to the second plane and back up, making a round trip.
Constructive Interference Condition:
For the reflected rays to constructively interfere, the path difference must be an integer multiple of the wavelength of the X-rays. That is, the extra path traveled by the rays reflecting from deeper planes should be equal to nλ, where λ is the wavelength of the X-rays, andn is an integer (the order of the diffracted beam).
Bragg’s Law Equation:
Setting the path difference equal to an integer multiple of the wavelength gives the condition for constructive interference:
nλ = 2dsinθ
Bragg’s Spectrometer
Bragg’s spectrometer, also known as a Bragg X-ray spectrometer, is an instrument used to measure the wavelengths of X-rays and to study the crystal structure of materials through X-ray diffraction. The spectrometer leverages Bragg’s Law to analyze the atomic and molecular structure of crystalline substances.
Design and Operation
Key Components of Bragg’s Spectrometer:
- X-ray Source: Produces the X-rays that are directed towards the crystal.
- Collimator: Narrows the X-ray beam before it strikes the crystal, ensuring that the X-rays hit the crystal at a specific angle.
- Crystal: The sample being studied. The crystal is mounted on a rotating table that allows precise adjustment of the angleθ at which X-rays strike the crystal.
- Detector: Measures the intensity of the diffracted X-rays. Detectors can rotate around the crystal to capture X-rays diffracted at various angles.
- Rotatable Table or Goniometer: Allows for precise measurement of the angles at which X-rays are incident and diffracted by the crystal.
Difference between Bragg’s law and diffraction
| Feature | Bragg’s Law | Diffraction |
|---|---|---|
| Definition | Bragg’s Law specifically describes the conditions under which X-rays are constructively interfered by the planes of a crystal lattice. | Diffraction refers to the bending and spreading of waves (like light, sound, or X-rays) when they encounter an obstacle or a slit that disrupts their path. |
| Focus | Focused on the angles and conditions for constructive interference in crystalline structures when exposed to X-rays. | Focuses on the general behavior of waves passing through gaps or around barriers. |
| Mathematical Expression | 𝑛𝜆 = 2𝑑sin𝜃, where 𝑛n is the order of diffraction, 𝜆 is the wavelength, 𝑑d is the interplanar spacing, and 𝜃 is the angle of incidence. | Various formulations depending on the context, but generally involves the wave equation and terms describing the geometry of the diffracting system. |
| Outcome | Produces specific angles (Bragg angles) where reflection peaks are observed due to constructive interference. | Produces a diffraction pattern that can include a wide range of phenomena including fringes, shadows, and intensity variations. |
| Experimental Setup | Requires a crystalline sample, X-ray source, detector, and precise angle measurement equipment. | Can be observed with various setups, from simple slits and barriers with waves to complex arrangements in scientific instruments. |
| Theoretical Basis | Based on the geometry of crystal lattices and the wave properties of X-rays. | Based on the principles of wave superposition and interference, applicable to any type of wave. |
Applications of Bragg’s Law
Material Analysis
- Crystal Structure Determination: Bragg’s Law is essential for identifying the atomic and molecular structure of crystalline substances. By analyzing the angles at which X-rays are diffracted by a material, scientists can deduce the spacing between the crystal planes and the arrangement of atoms within the crystal.
Industrial Applications
- Quality Control: In industries that require precise crystal formations such as semiconductors and metallurgy, Bragg’s Law helps in checking the quality and purity of materials by examining their crystal structure.
Scientific Research
- Pharmaceuticals: Bragg’s Law aids in the development of new drugs by understanding the crystal structure of chemical compounds, which is crucial for designing drugs with desired properties and efficacies.
- Nanotechnology: The law is used to explore and manipulate materials at the nanoscale, leading to innovations in electronics, optics, and materials science.
Educational Tools
- Teaching and Learning: Bragg’s Law provides a foundational concept for students learning about the properties of X-rays and crystallography, helping them understand the underlying principles of wave interference and material science.
Examples of Braggs Law
1. Determining Crystal Structures in Chemistry
In chemistry, Bragg’s Law is used to determine the crystal structure of various chemical compounds. For instance, determining the structure of salt (sodium chloride) involves directing X-rays of a known wavelength at a salt crystal and using Bragg’s Law to calculate the spacing between the sodium and chloride ions based on the angles at which the X-rays are diffracted.
2. Studying Metals in Material Science
Material scientists use Bragg’s Law to study the crystal structures of metals and alloys. This can help in understanding the properties of the material, such as its strength, ductility, and heat resistance. For example, by studying the diffraction pattern of steel, researchers can gain insights into how different alloying elements affect its microstructure and properties.
3. Pharmaceuticals: Analyzing Drug Compounds
In the pharmaceutical industry, Bragg’s Law is crucial for analyzing the crystal form of drug compounds. Different crystal forms can have different stability, solubility, and bioavailability. For example, the crystal structure of aspirin has been studied to understand its different polymorphic forms, which can affect how the drug is absorbed in the body.
4. Biology: Protein Crystallography
Bragg’s Law is fundamental in the field of protein crystallography, where it is used to determine the three-dimensional structures of proteins and other biological macromolecules. Understanding the structure of a protein can provide crucial insights into its function and how it interacts with other molecules. For example, the structure of the enzyme lysozyme was determined using X-ray crystallography, which helped in understanding its antibacterial mechanism.
5. Geology: Mineral Identification
Geologists use Bragg’s Law to identify minerals based on their crystal structures. This can be important in mining, as the value of rocks can depend heavily on their mineral content. By analyzing the diffraction patterns obtained from a mineral sample, geologists can identify the minerals present and their abundance.
FAQs
Why is Bragg’s Law important?
Bragg’s Law is crucial for determining the crystal structure of materials. It helps scientists understand the molecular arrangement within a crystal by analyzing how it diffracts X-rays at different angles.
Can Bragg’s Law be applied to any material?
Bragg’s Law applies to crystalline materials where atoms are periodically arranged in a regular lattice. It does not apply to amorphous solids or liquids where long-range order is absent.
What are the limitations of Bragg’s Law?
The main limitation of Bragg’s Law is that it assumes perfect crystalline order and does not account for defects or imperfections in the crystal which can affect the diffraction pattern.
What does 𝑛n represent in Bragg’s Law?
In Bragg’s Law, 𝑛n represents the order of the diffracted beam, which is an integer that multiples the path difference between the waves reflecting off successive crystal planes, leading to constructive interference.
Share :
Practice Test
In Bragg's Law, what does the symbol λ represent?
Angle of incidence
Order of reflection
Wavelength of the incident wave
Distance between crystal planes
of 10
What is the role of the angle θ in Bragg's Law?
It represents the distance between crystal planes
It is the angle between the incident wave and the crystal plane
It is the angle between the reflected wave and the crystal plane
It is the angle of incidence
of 10
What does the symbol 'd' represent in Bragg's Law?
Wavelength
Angle of incidence
Distance between crystal planes
Order of reflection
of 10
How is the order of reflection (n) in Bragg's Law determined?
It is always equal to 1
It is the ratio of the wavelength to the distance between crystal planes
It is an integer representing the number of wavelengths that fit into the path difference
It is the sine of the angle of incidence
of 10
If the wavelength of the incident wave is 0.1 nm and the distance between crystal planes is 0.2 nm, at what angle will the first-order reflection occur?
15°
30°
45°
60°
of 10
In X-ray diffraction, why is Bragg's Law important?
It determines the intensity of reflected X-rays
It calculates the speed of X-rays
It predicts the angles at which X-rays are constructively reflected
It measures the energy of X-rays
of 10
How does increasing the wavelength of the incident wave affect the angle of incidence for a given crystal plane spacing and order of reflection?
It decreases the angle
It increases the angle
It does not affect the angle
It changes the distance between crystal planes
of 10
If nλ = 2d sinθ, what is the condition for constructive interference of reflected waves?
The path difference must be an odd multiple of the wavelength
The path difference must be an even multiple of the wavelength
The path difference must be equal to the wavelength
The path difference must be an integer multiple of the wavelength
of 10
What is the significance of the order of reflection (n) in Bragg's Law?
It indicates the number of crystal planes involved
It specifies the number of wavelengths fitting into the path difference
It determines the angle of reflection
It defines the wavelength of the incident wave
of 10