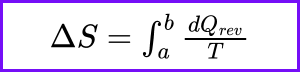What does Carnot’s theorem state about the efficiency of a heat engine?
The efficiency of a heat engine depends only on the working substance used
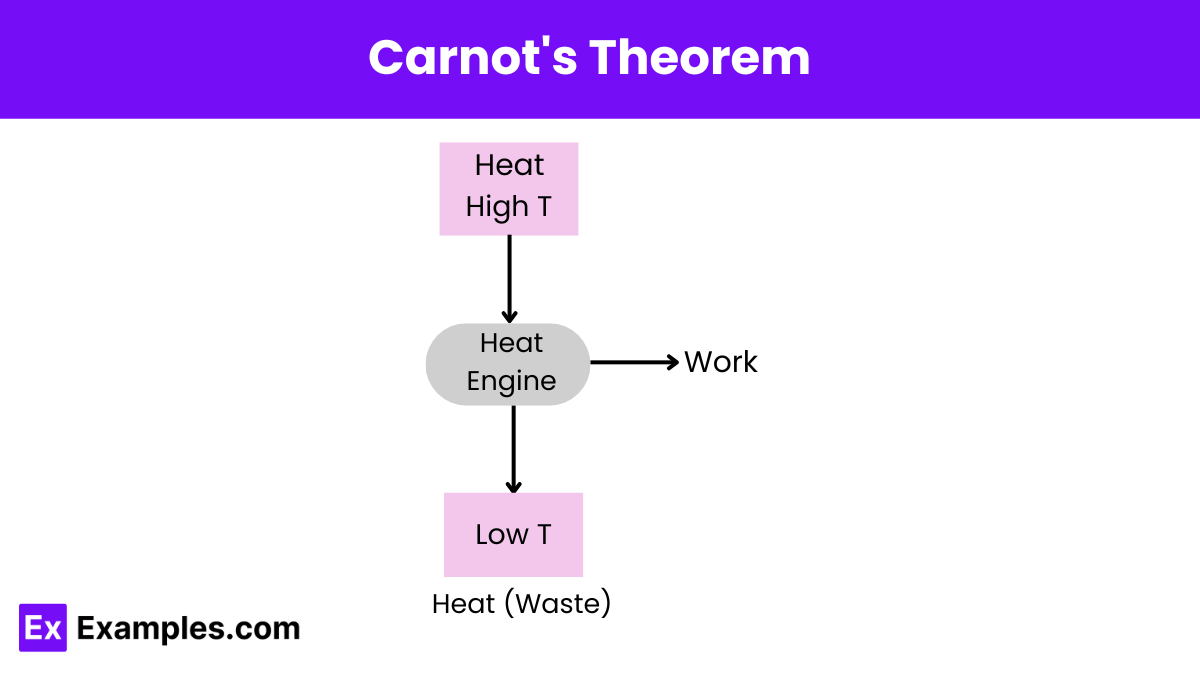
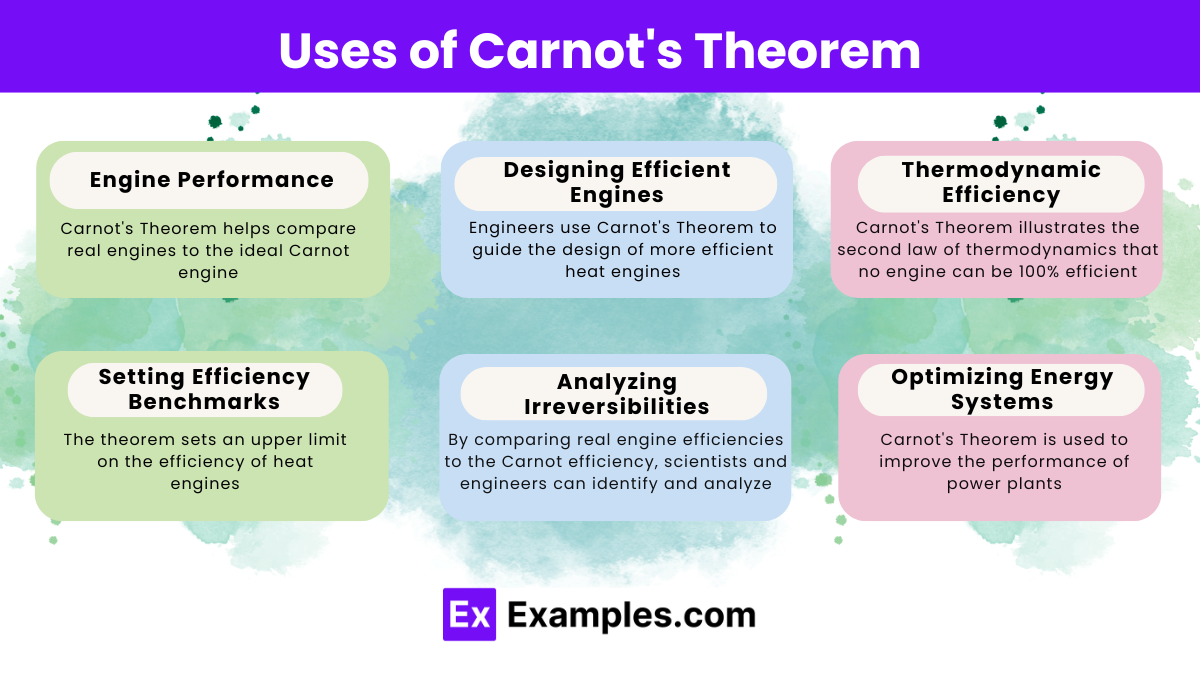
No heat engine working between two heat reservoirs can be more efficient than a Carnot engine operating between the same reservoirs
The efficiency of a heat engine is always 100%
Efficiency increases with the increase in the engine’s size