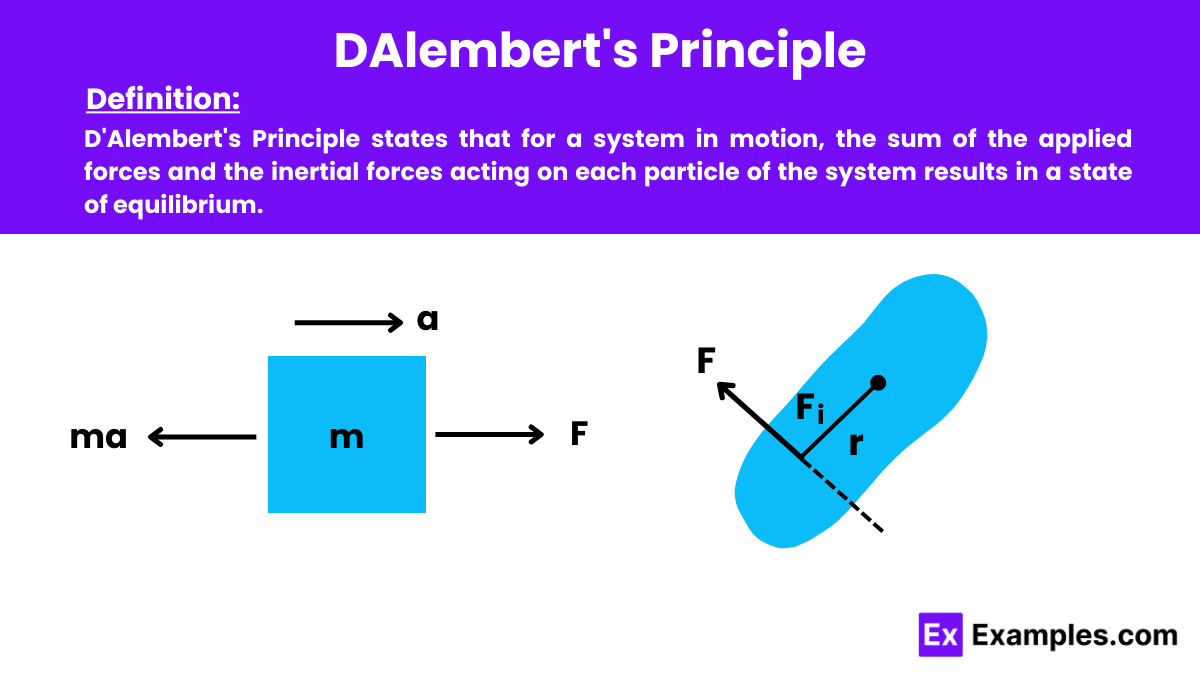
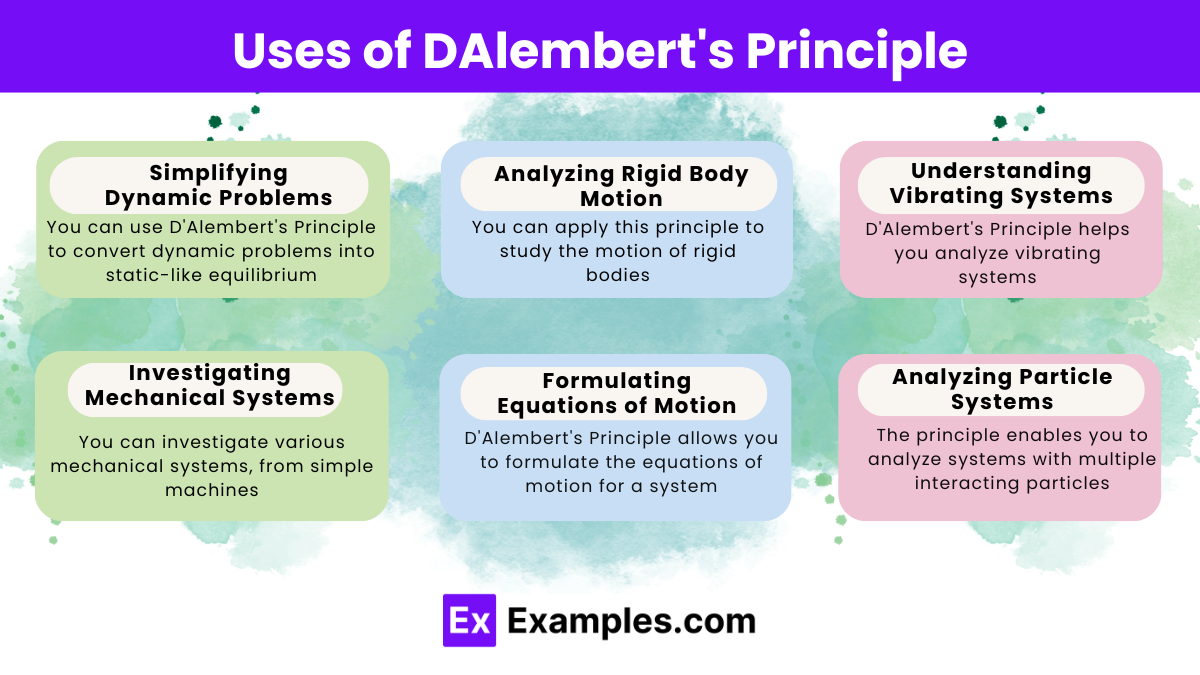
Which of the following best describes D'Alembert's Principle?
The sum of forces on a body is zero.
The difference between applied forces and inertial forces is zero.
The sum of moments about any point is zero.
The difference between kinetic and potential energy is zero.