Derivation of One Dimensional Wave Equation

The one-dimensional wave equation is fundamental in understanding wave phenomena in various fields such as acoustics, electromagnetics, and fluid dynamics. It describes how waves propagate in a medium over time. The derivation starts from Newton’s second law applied to a small segment of a vibrating string. By considering the forces due to tension and the resulting acceleration, we can express the transverse displacement as a function of position and time. This approach leads to the formation of a partial differential equation that characterizes wave motion

What are One Dimensional Waves?

One-dimensional waves are characterized by their propagation in a single spatial dimension, with time being the primary independent variable. These waves can be observed in various phenomena, such as sound waves, ocean waves, vibrations from musical instruments, and electromagnetic radiation. In classical physics, waves are studied within the realms of mechanics, acoustics, and optics.

A wave is defined as a disturbance that travels through a medium, transferring energy from one point to another. When the disturbance is singular, it is referred to as a pulse. When the disturbance is repetitive, it is known as a periodic wave. The medium through which the wave travels consists of a series of interconnected particles. These particles exhibit wave-like behavior by interacting with each other, which enables the disturbance to propagate through the medium.

Types of Waves

Mechanical Waves : Mechanical waves require a medium to travel through, such as air, water, or solids. Examples include sound waves, ocean waves, and seismic waves. These waves propagate by causing the particles of the medium to oscillate.

Electromagnetic Waves : Electromagnetic waves do not require a medium and can travel through a vacuum. They are produced by the oscillation of electric and magnetic fields. Examples include light waves, radio waves, and X-rays.

Transverse Waves : In transverse waves, the particles of the medium move perpendicular to the direction of wave propagation. Examples include waves on a string and electromagnetic waves.

Longitudinal Waves : Longitudinal waves have particles that oscillate parallel to the direction of wave travel. Sound waves in air and compression waves in a slinky are typical examples.

Surface Waves : Surface waves travel along the interface between two different media, such as air and water. Ocean waves are a common example, combining both transverse and longitudinal motion.

The Wave Equation

The wave equation is a fundamental mathematical description of how waves propagate through a medium. It is a partial differential equation that relates the spatial and temporal variations of a wave. In one dimension, the wave equation is given by:

∂²y/∂t² = v²∂²y/∂x²

where 𝑦(𝑥,𝑡) represents the displacement of the wave at position x and time t, and 𝑣 is the speed of the wave. This equation applies to both mechanical and electromagnetic waves and is crucial for understanding wave behavior in various physical contexts.

One-Dimensional Wave Equation Derivation

The one-dimensional wave equation describes how waves propagate along a string or similar medium. This derivation uses Newton’s second law and principles of calculus.

Step 1: Consider a Small Segment of the String

Take a small segment of the string with length Δx. Let T be the tension in the string, which is assumed to be constant. The segment experiences forces due to the tension at its ends.

Step 2: Analyze the Forces

The vertical components of the tension at the ends of the segment can be expressed as:
Tsin(θ1) ≈ T∂y/∂x∣ₓ

𝑇sin(𝜃2) ≈ 𝑇∂𝑦/∂𝑥∣ₓ₊Δₓ

​where ( θ1​ ) and ( θ2 ) are the angles the string makes with the horizontal at ( x ) and ( x +Δx ), respectively. For small angles, sin(θ) ≈ tan(θ).

Step 3: Net Force on the Segment

The net vertical force ( F ) on the segment is:
F = 𝑇∂𝑦/∂𝑥∣ₓ₊Δₓ ] – T∂y/∂x∣ₓ

Using the definition of the derivative:
[ F = T 𝑇∂𝑦/∂𝑥∣ₓ₊Δₓ ] – ∂y/∂x∣ₓ ≈ T∂²y/∂x²Δₓ

Step 4: Apply Newton’s Second Law

According to Newton’s second law, the net force is equal to the mass of the segment times its acceleration:
F=m∂²𝑦/∂t²

The mass ( m ) of the segment is:
m = ∂Δx

where ( ∂ ) is the mass per unit length. Therefore:
∂²y/∂x² = ∂²y/∂t²

Step 5: Simplify the Equation

Divide through by (Δₓ )
∂²y/∂x² = μ∂²y/∂t²

Step 6: Final Form of the Wave Equation

Rearrange to get the standard form of the one-dimensional wave equation:
∂²y/∂t² = ∂²y/∂x²

Define the wave speed ( v ) as:
v = √t/μ​​

Thus, the wave equation becomes:
∂²y/∂t² = v²∂²y/∂x²

This equation describes the propagation of waves along a string or similar medium, where ( v ) is the speed of the wave, ( y(x,t) ) is the displacement, ( x ) is the position, and ( t ) is the time.

Hooke’s Law

Hooke’s Law is a fundamental principle in physics that describes the behavior of springs and other elastic materials. It states that the force required to extend or compress a spring by some distance is proportional to that distance. Mathematically, Hooke’s Law is expressed as:

𝐹=−𝑘𝑥

where:

• 𝐹 is the force applied to the spring,
• 𝑘 is the spring constant (a measure of the stiffness of the spring),
• 𝑥 is the displacement from the spring’s equilibrium position.

Uses of the One-Dimensional Wave Equation

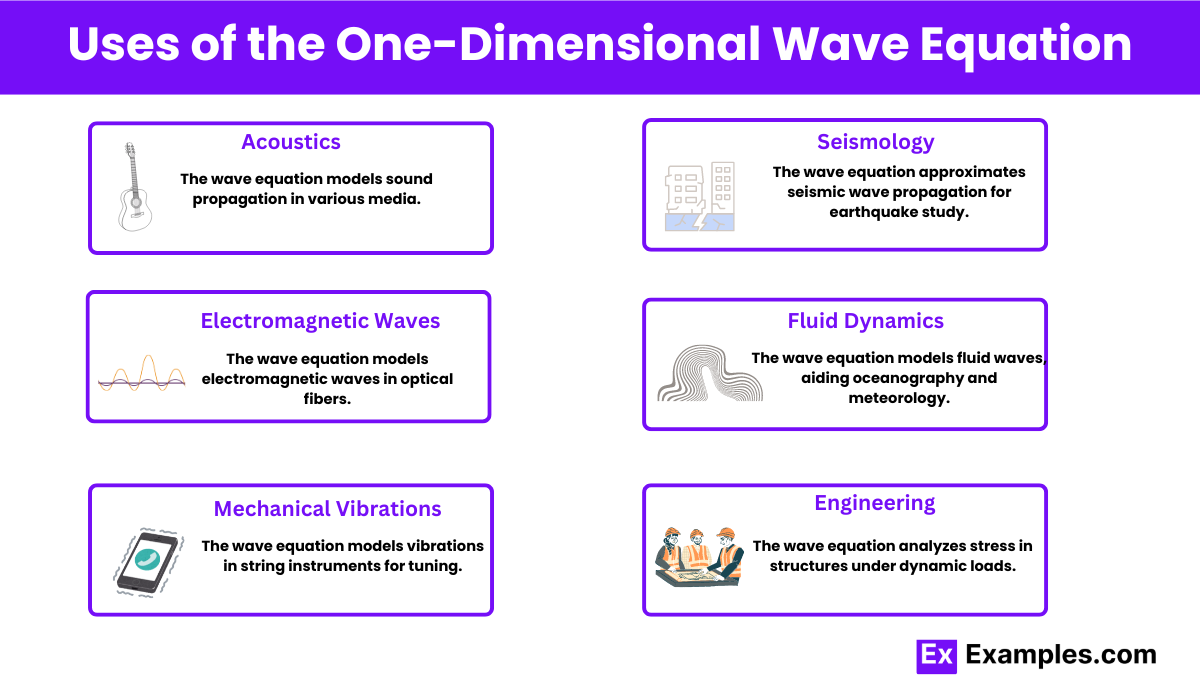
Acoustics : The wave equation describes how sound waves propagate through different media, such as air, water, and solids. It helps in designing acoustical systems, musical instruments, and understanding speech and hearing.

Electromagnetic Waves : The wave equation is used to understand the propagation of electromagnetic waves in one-dimensional structures like optical fibers and waveguides. This is essential in telecommunications and fiber-optic technologies.

Mechanical Vibrations : The wave equation models the vibrations of strings in musical instruments like guitars and pianos. It helps in designing and tuning these instruments for desired sound quality.

Seismology : The propagation of seismic waves through the Earth can be approximated using the one-dimensional wave equation. This aids in the study of earthquakes and the structure of the Earth’s interior.

Fluid Dynamics : The wave equation is used to model waves in fluids, such as waves on the surface of water and internal waves within ocean layers. This has applications in oceanography and meteorology.

Engineering : Engineers use the wave equation to analyze the stress and strain in structures subjected to dynamic loads, such as bridges and buildings during earthquakes or wind loads.

Derivation of One-Dimensional Wave Equation Examples

Vibrating String

To derive the one-dimensional wave equation for a vibrating string, we start by considering a small segment of the string with a given length and constant tension. The vertical components of the tension at the ends of this segment can be approximated by considering how the displacement changes along the string. The net vertical force acting on this segment is the difference between these components. Using Newton’s second law, we equate this net force to the mass of the segment times its acceleration. By simplifying and dividing by the segment length, we derive the wave equation, which describes how waves propagate along the string.

Sound Waves in a Tube

For sound waves in a tube, consider a small segment of air within a long, narrow tube. The net force on this air segment arises from pressure differences at its ends. This force can be expressed using the pressure gradient and the tube’s cross-sectional area. Applying Newton’s second law, we relate this net force to the mass of the air segment and its acceleration. By using the relationship between pressure variations and particle displacement, we substitute into our equation and simplify. This leads to the wave equation for sound waves, which describes how sound propagates through the air in the tube.

Faqs