Derivation of Van der Waals Equation with Derivations & Examples

Derivation of Van der Waals Equation with Derivations & Examples

The Van der Waals equation is a significant enhancement of the ideal gas law, developed to account for the real behavior of gases. While the ideal gas law, (PV = nRT), assumes that gas molecules do not interact and occupy no volume, these assumptions fall short under high-pressure and low-temperature conditions. Johannes Diderik van der Waals introduced corrections to address these limitations. The derivation of the Van der Waals equation incorporates two essential factors: the finite size of gas molecules and the intermolecular attractive forces.

The equation introduces two parameters, (a) and (b), where (a) corrects for the intermolecular forces, and (b) accounts for the finite volume occupied by gas molecules. The corrected volume is represented as (V – nb), and the adjusted pressure includes an additional term, (an²/Van²), reflecting the intermolecular attractions. Combining these corrections with the ideal gas law, we obtain the Van der Waals equation:

[ (P + an²/V²) (V-nb) = nRT ]

This equation provides a more accurate description of gas behavior, particularly under non-ideal conditions, making it crucial for various scientific and industrial applications, from chemical engineering to environmental science.

Van der Waals Equation Derivation

The Van der Waals equation improves upon the ideal gas law by accounting for the real behavior of gases, particularly at high pressures and low temperatures. This derivation introduces two critical corrections to the ideal gas law: one for the volume occupied by gas molecules and another for the intermolecular forces between them.

Step-by-Step Derivation

1.Ideal Gas Law

PV = nRT

The Ideal Gas Law is given by:

where:

• (P) is the pressure,

• (V) is the volume,

• (n) is the number of moles,

• (R) is the universal gas constant,

• (T) is the temperature.

2. Correct for the Volume of Gas Molecules:
Real gas molecules occupy a finite volume, which becomes significant at high pressures. Let (b) be the volume excluded by a mole of gas due to the finite size of the molecules. Thus, the effective volume available for gas molecules to move in is (V – nb), where (n) is the number of moles:
Vₑբբₑ꜀ₜᵢᵥₑ = V – nb

3. Correct for Intermolecular Forces:
In real gases, attractive forces between molecules reduce the impact of collisions on the container walls, effectively reducing the pressure. The reduction in pressure is proportional to the square of the molar concentration of the gas, (n/b)², and the constant of proportionality is (a). Therefore, the corrected pressure is:
[Pₑբբₑ꜀ₜᵢᵥₑ = P + an²/V² ]

4. Combine the Corrections with the Ideal Gas Law:
Substitute the corrected pressure and volume into the ideal gas law:
(P + an²/V²) (V – nb) = nRT

5. Simplify the Expression:
Expand and rearrange the equation to make it clearer:
P(V – nb) + an²/V² (V-nb) = nRT
Simplifying further, we get:
P(V – nb) +an²/V – an³b/V² = NRT

6. Van der Waals Equation for One Mole of Gas:
For simplicity, consider one mole of gas ((n = 1)):
( P + a/V²) (V – b) = RT

7.General Form of Van der Waals Equation:
For (n) moles of gas, the equation becomes:
( P + an²/V²) (V – nb) = nRT

What is the Van der Waals Equation?

The Van der Waals equation is a thermodynamic equation of state that describes the behavior of real gases. It is an improvement upon the ideal gas law, which assumes that gas molecules do not interact and have no volume. The Van der Waals equation introduces corrections for these assumptions, providing a more accurate representation of gas behavior under various conditions, especially at high pressures and low temperatures.

The Equation

The Van der Waals equation is expressed as:

( P + an²/V²) (V – nb) = nRT

where:

• (P) is the pressure of the gas,

• (V) is the volume of the gas,

• (n) is the number of moles of the gas,

• (R) is the universal gas constant ((8.314 /mol\cdotpK),

• (T) is the temperature in Kelvin,

• (a) is a constant that accounts for the attractive forces between molecules,

• (b) is a constant that accounts for the finite volume occupied by gas molecules.

Components of the Van der Waals Equation

Pressure Correction (an²/V²):

• The term (an²/V²) accounts for the intermolecular attractive forces. In real gases, these forces reduce the pressure exerted on the walls of the container, as molecules are pulled towards each other. The constant (a) varies depending on the type of gas.

Volume Correction (V – nb):

• The term (V – nb) corrects for the volume occupied by gas molecules themselves. In the ideal gas law, it is assumed that gas molecules do not occupy any volume, but in reality, they do. The constant (b) represents the effective volume occupied by one mole of gas molecules and is specific to each gas.

Significance and Applications

The Van der Waals equation is significant because it provides a more realistic model for the behavior of gases compared to the ideal gas law. It is especially useful in scenarios where gases are not ideal, such as at high pressures or low temperatures. Some applications include:

• Chemical Engineering: Design and optimization of processes involving gases, such as reaction kinetics, distillation, and gas liquefaction.

• Material Science: Studying gas adsorption on surfaces and the behavior of gases in confined spaces.

• Environmental Science: Modeling the behavior of atmospheric gases and pollutants.

• Industrial Processes: Predicting the properties of gases during storage and transportation.

Derivation of Van Der Waals Equation For Real Gases

Here’s a step-by-step derivation of the Van der Waals equation for real gases:

1. Start with the Ideal Gas Law

The ideal gas law is given by:

[ PV = nRT ]

2. Correcting for Molecular Volume

In reality, gas molecules occupy a finite volume. Therefore, the volume available for the gas molecules to move in is less than the volume of the container. Let ( b ) be the volume occupied by one mole of gas molecules. The corrected volume ( V’ ) is:

[ V’ = V – nb ]

where ( n ) is the number of moles.

3. Correcting for Intermolecular Attractions

Real gas molecules experience intermolecular attractions, which reduce the pressure exerted on the walls of the container. Van der Waals introduced a term to account for these attractions. Let ( a ) be a constant that measures the strength of these attractions. The corrected pressure ( P’ ) is:

( P’ = P + an²/V² )

4. Substitute Corrections into the Ideal Gas Law

Replace the pressure ( P ) and volume ( V ) in the ideal gas law with the corrected pressure ( P’ ) and corrected volume ( V’ ):

( P + an²/V² ) ( V – nb )

5. Van der Waals Equation

Simplifying the above expression, we obtain the Van der Waals equation for real gases:

( P + an²/V² ) ( V – nb )

Van Der Waals Derivation For One Mole of Gas

To derive the Van der Waals equation for one mole of gas, we start with the Ideal Gas Law and introduce corrections for the finite size of gas molecules and intermolecular forces.

1. The ideal gas law

The ideal gas law relates pressure, volume, temperature, and moles of gas, assuming no intermolecular forces or molecular volume: ( PV = nRT ).

2. Correction for Intermolecular Forces

In a real gas, attractive intermolecular forces reduce the effective pressure exerted by the gas molecules on the walls of the container. This reduction in pressure can be accounted for by adding a term (\frac{a}{V_m^2}) to the pressure, where ( a ) is a constant specific to the gas that represents the magnitude of the intermolecular forces. Therefore, the corrected pressure is:

[PᵢDₑₐₗ = P +a/V²ₘ ]

3. Correction for Finite Molecular Size

In an ideal gas, the volume occupied by the gas molecules themselves is negligible. However, in a real gas, the finite size of the molecules means that not all of the volume of the container is available for the gas molecules to move around in. This is accounted for by subtracting a term ( b ), the volume occupied by one mole of gas molecules, from the molar volume ( V_m ). Therefore, the corrected volume is:

[ Vₑբբ = Vₘ – b ]

4. Combining the Corrections

We now combine these corrections into the Ideal Gas Law. The corrected pressure ( PᵢDₑₐₗ ) and the corrected volume ( Vₑբբ ) are substituted into the Ideal Gas Law:

[ PᵢDₑₐₗ Vₑբբ = RT ]

Substitute ( PᵢDₑₐₗ and Vₑբբ ):

(P + a/V²ₘ) (Vₘ – b) = RT

This is the Van der Waals equation for one mole of a real gas.

Uses of the Derivation of the Van der Waals Equation

Download Uses of the Derivation of the Van der Waals Equation Pdf

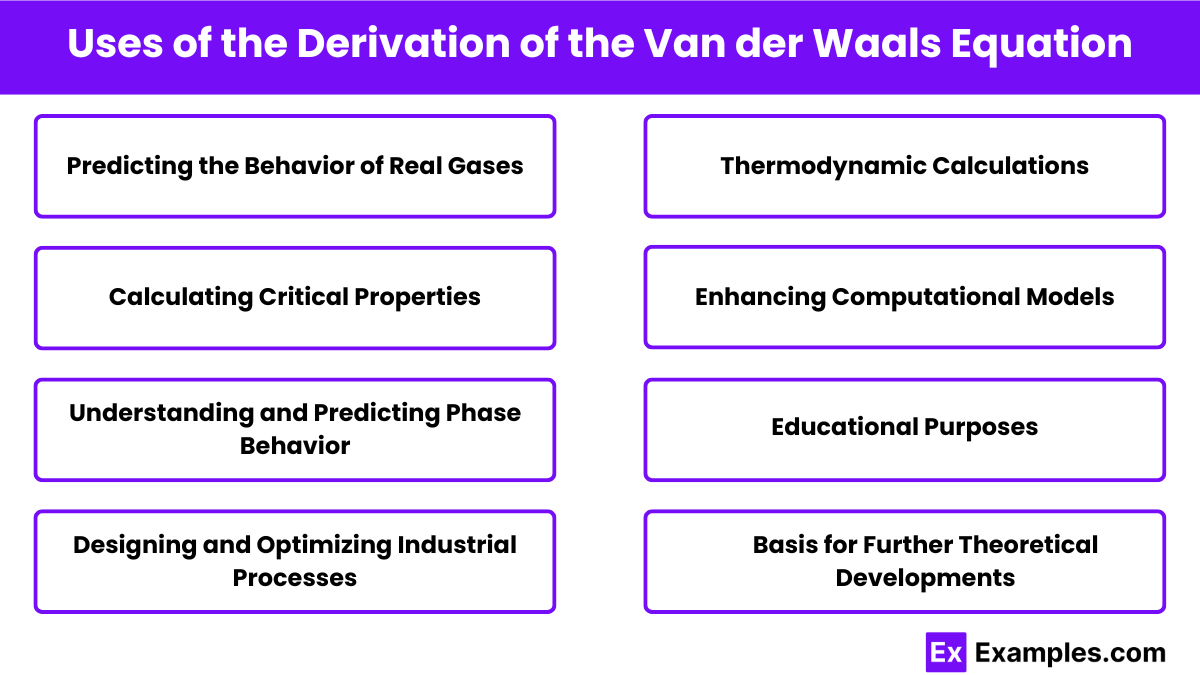
The derivation of the Van der Waals equation has several important uses in the field of physical chemistry and engineering. Here are some key applications:

• Predicting the Behavior of Real Gases : The Van der Waals equation improves the accuracy of predictions about the behavior of real gases, especially under conditions where the Ideal Gas Law fails (e.g., high pressures and low temperatures). It accounts for the volume occupied by gas molecules and the intermolecular forces between them, providing a more realistic model for real gases.

• Calculating Critical Properties : The Van der Waals equation can be used to determine critical properties of gases, such as the critical temperature, critical pressure, and critical volume. These properties are essential for understanding phase transitions and designing equipment for processes involving gases and liquids.

• Designing and Optimizing Industrial Processes : In industries such as chemical engineering and petroleum engineering, the Van der Waals equation is used to model and optimize processes involving gases and liquids. This includes the design of reactors, separators, and pipelines, where accurate predictions of gas behavior under varying conditions are crucial.

• Understanding and Predicting Phase Behavior : The equation helps in understanding phase behavior of substances, including the conditions under which gases condense into liquids and the formation of supercritical fluids. This is particularly important in the study of phase diagrams and in applications like supercritical fluid extraction.

• Thermodynamic Calculations : The Van der Waals equation is used in thermodynamic calculations to derive other important properties of gases, such as internal energy, enthalpy, entropy, and free energy. These properties are fundamental to the analysis of energy changes and efficiencies in thermodynamic cycles and processes.

• Enhancing Computational Models : In computational chemistry and molecular dynamics simulations, the Van der Waals equation serves as a foundation for more complex models that describe intermolecular interactions. This helps in predicting the behavior of substances at the molecular level, which is vital for research and development in materials science and drug design.

• Educational Purposes : The derivation of the Van der Waals equation is an important part of the curriculum in physical chemistry and chemical engineering courses. It provides students with a deeper understanding of the limitations of the Ideal Gas Law and the corrections needed to describe real gas behavior.

Examples of the Derivation of the Van der Waals Equation

• Volume Correction : Real gas molecules occupy space, reducing the effective volume available for motion compared to ideal gases.

• Pressure Correction : Intermolecular attractions in real gases lower the force exerted on container walls, compared to the ideal gas assumption of no attractions.

• High Pressure : At high pressures, real gases deviate significantly from ideal behavior due to increasedmolecular interactions and reduced free volume.

• Low Temperature : At low temperatures, intermolecular attractions become significant, causing real gases to deviate from ideal gas predictions.

• Liquefaction : The Van der Waals equation explains the liquefaction of gases by accounting for intermolecular forces and molecular volume, unlike the ideal gas law.

What does the Van der Waals equation describe?

The Van der Waals equation describes the behavior of real gases by accounting for molecular size and intermolecular forces.

What do the constants a and b represent in the Van der Waals equation?

In the Van der Waals equation, 𝑎a represents the magnitude of intermolecular forces, and 𝑏b accounts for the finite size of molecules.

Why is the Van der Waals equation important?

The Van der Waals equation is important because it provides a more accurate description of the behavior of real gases compared to the Ideal Gas Law.

How is the Van der Waals equation derived?

The Van der Waals equation is derived by modifying the Ideal Gas Law to include terms for molecular volume and intermolecular forces.

How does the Van der Waals equation improve upon the Ideal Gas Law?

The Van der Waals equation improves upon the Ideal Gas Law by providing a more realistic model for gas behavior under non-ideal conditions.

Why does the Van der Waals equation include a term for molecular volume?

The Van der Waals equation includes a term for molecular volume to account for the space occupied by gas molecules themselves.

How does the Van der Waals equation affect predictions of gas behavior?

The Van der Waals equation provides more accurate predictions of gas behavior under high-pressure and low-temperature conditions.

How are the constants a and b determined for a particular gas?

The constants a and b are determined experimentally for each specific gas.

What does 𝑉ₘ​ represent in the Van der Waals equation?

In the Van der Waals equation, 𝑉ₘ​ represents the molar volume of the gas.

What does R represent in the Van der Waals equation?

In the Van der Waals equation, R represents the universal gas constant.