Diffraction Grating Formula

What is Diffraction Grating Formula?

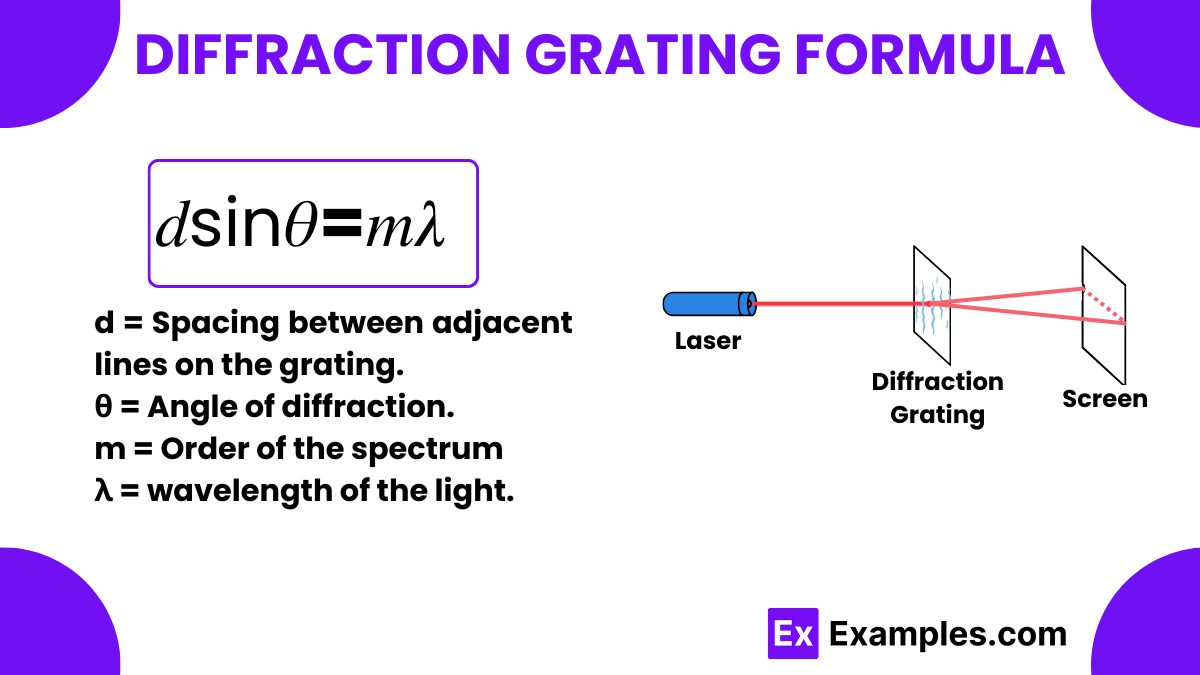
A diffraction grating is an optical component with a regular pattern of closely spaced lines or slits, which diffracts light into several beams traveling in different directions. The fundamental physics governing the behavior of light as it passes through a diffraction grating is encapsulated in the diffraction grating formula. This formula calculates the angles at which light rays spread out after passing through the grating. It can represent as

𝑑sin⁡𝜃=𝑚𝜆

• d is the spacing between adjacent lines on the grating.
• θ is the angle of diffraction.
• m is the order of the spectrum, which can be any whole number.
• λ is the wavelength of the light.

The concept and mathematical description of diffraction gratings were developed by the American physicist David Rittenhouse in 1785. His early experiments, which involved looking at the spectra created by light diffraction through bird feathers, paved the way for later, more refined techniques. This formula helps scientists and engineers design grating to precisely control light dispersion in spectrometers, telescopes, and other optical devices, making it a cornerstone in the field of optics within physics.

Applications of Diffraction Grating Formula

1. Spectroscopy: Scientists use the diffraction grating formula to design spectrometers for analyzing the wavelengths of light emitted or absorbed by materials. This helps in identifying chemical substances and determining their properties.
2. Optical Engineering: Engineers apply the formula to create high-precision optical components such as lasers and optical fibers. These components require precise light manipulation capabilities.
3. Astronomy: Astronomers employ diffraction gratings to separate starlight into its spectral components. This separation allows them to determine the composition, temperature, and movement of celestial objects.
4. Telecommunications: In telecommunications, the diffraction grating formula aids in the design of optical components that improve the efficiency and capacity of data transmission systems.
5. Educational Tools: In education, diffraction gratings serve as excellent tools for demonstrating wave behavior and the fundamental principles of wave-particle duality in physics courses.

Example Problems on Diffraction Grating Formula

Problem 1: Basic Calculation

Question: A diffraction grating has 5000 lines per centimeter. Find the angle at which the first-order maximum (m = 1) will occur for light with a wavelength of 600 nm.

Solution:

Step 1: Calculate the line spacing 𝑑d. Since there are 5000 lines/cm, convert cm to meters for consistency:

𝑑=1 cm / 5000 lines = 0.01 m / 5000 = 2×10⁻⁶ m=2000 nm;

Step 2: Use the diffraction grating formula 𝑑sin⁡𝜃 = 𝑚𝜆

2000 nm × sin⁡𝜃 = 1×600 nm

Step 3: Solve for θ:

sin⁡𝜃=600 nm / 2000 nm=0.3​

𝜃=sin⁡−1(0.3)≈17.5.

Conclusion: The First-order maximum for 600 nm light occurs at approximately 17.5 degrees.

Problem 2: Higher Order Maxima

Question: If the same grating is used, at what angle will the second-order maximum (m = 2) occur for the same wavelength of light?

Solution:

Step 1: Use the same line spacing 𝑑=2000 nm and apply the Diffraction grating formula:

2000 nm × sin⁡𝜃 = 2×600 nm=1200 nm.

Step 2: Solve for θ:

sin⁡𝜃=1200 nm / 2000 nm=0.6

𝜃=sin⁡−1(0.6)≈36.9.

Conclusion: The Second-order maximum for 600 nm light occurs at approximately 36.9 degrees.

FAQs

What is D in Double Slit Formula?

In the double slit formula, D represents the distance between the two slits, crucial for calculating the interference pattern.

What is the Main Idea of Diffraction Grating?

The main idea of a diffraction grating is to separate light into its component wavelengths by interference, providing detailed spectral analysis.

How Do You Calculate D in Diffraction Grating?

To calculate D in a diffraction grating, divide the length of the grating by the total number of slits to get the spacing between them.