What is the Ideal Gas Law equation?
PV = nRT
PV = nR/T
P/V = nRT
P = nRT/V
of 10
Ideal Gas Law – Examples, Definition, Formula, Uses, FAQ’s
Ideal Gas Law – Examples, Definition, Formula, Uses, FAQ’s
The Ideal Gas Law is a fundamental principle in physics that describes the behavior of ideal gases. It combines several individual gas laws into one comprehensive equation. This law is pivotal in understanding how gases respond to changes in pressure, volume, and temperature.
What is Ideal Gas Law?
Formula of Ideal Gas Law
The formula for the Ideal Gas Law is:
Where:
- P is the pressure of the gas.
- V is the volume of the gas.
- n is the number of moles of the gas.
- R is the universal gas constant.
- T is the temperature of the gas in Kelvin.
Ideal Gas Law Units
| Quantity | Symbol | SI Unit | Common Unit(s) | Description |
|---|---|---|---|---|
| Pressure | 𝑃 | Pascal (Pa) | atm, mmHg, Torr | Force per unit area |
| Volume | 𝑉 | Cubic meter (m³) | Litre (L) | Space occupied by the gas |
| Number of Moles | 𝑛 | Mole (mol) | Amount of substance | |
| Ideal Gas Constant | R | Joules per mole per Kelvin (J/(mol·K)) | L·atm/(mol·K), cal/(mol·K) | Proportionality constant in the Ideal Gas Law |
| Temperature | T | Kelvin (K) | Celsius (°C) | Measure of the thermal energy |
Derivation of Ideal Gas Law
The Ideal Gas Law is derived from combining several empirical gas laws: Boyle’s Law, Charles’s Law, and Avogadro’s Law. These laws describe the relationships between pressure, volume, temperature, and the number of moles of a gas. Here is a step-by-step derivation.
Boyle’s Law
Boyle’s Law states that the pressure of a gas is inversely proportional to its volume when the temperature and the number of moles are constant. 𝑃∝1/𝑉 or 𝑃𝑉=𝑘₁ where 𝑘₁ is a constant for a given amount of gas at a constant temperature.
Charles’s Law
Charles’s Law states that the volume of a gas is directly proportional to its temperature when the pressure and the number of moles are constant. 𝑉∝𝑇 or 𝑉/𝑇 = 𝑘₂ where 𝑘₂ is a constant for a given amount of gas at a constant pressure.
Avogadro’s Law
Avogadro’s Law states that the volume of a gas is directly proportional to the number of moles of gas when the pressure and temperature are constant. 𝑉∝𝑛 or 𝑉/n = 𝑘₃ where 𝑘₃ is a constant for a given pressure and temperature.
Combining the Laws
To derive the Ideal Gas Law, we combine Boyle’s, Charles’s, and Avogadro’s Laws. We know that: 𝑉∝𝑛𝑇/𝑃 This implies: 𝑉=𝑘₄𝑛𝑇/P where 𝑘₄ is a proportionality constant.
Rearranging the equation gives us: 𝑃𝑉=𝑘₄𝑛T
The constant 𝑘₄ is universal and is known as the ideal gas constant, R. Therefore, we write:
𝑃𝑉=𝑛𝑅𝑇
Relationship between Pressure and Temperature
The relationship between pressure and temperature of a gas is described by Gay-Lussac’s Law. This law states that the pressure of a fixed amount of gas at constant volume is directly proportional to its absolute temperature.
Gay-Lussac’s Law indicates that when the volume and the number of moles of a gas are constant, the pressure of the gas increases with an increase in temperature and decreases with a decrease in temperature.
Gay-Lussac’s Law provides a clear and direct relationship between the pressure and temperature of a gas at constant volume. Understanding this relationship is crucial in various practical applications, such as cooking and the safe handling of pressurized containers.
Uses of Ideal Gas Law
- Determining Gas Properties: You can use the Ideal Gas Law to calculate any one of the four variables (pressure, volume, temperature, or number of moles) if the other three are known. This is useful in laboratory settings for various experiments involving gases.
- Chemical Reactions Involving Gases: In stoichiometry, the Ideal Gas Law helps you calculate the volumes of gases involved in chemical reactions. Knowing the amount of reactants or products allows you to predict the volume of gas produced or consumed, aiding in the design of chemical processes.
- Diving and Hyperbaric Medicine: The Ideal Gas Law explains how gases behave under different pressures, which is crucial for understanding the effects of pressure changes on divers. It helps in treating conditions like decompression sickness by predicting how gases will dissolve and come out of solution in the body.
- Engineering Applications: Engineers use the Ideal Gas Law in designing and operating equipment such as internal combustion engines, refrigeration systems, and air conditioning units. It helps predict how gases will behave under different conditions, ensuring optimal performance of these systems.
- Meteorology and Atmospheric Science: The Ideal Gas Law is fundamental in modeling and understanding atmospheric processes. Meteorologists use it to predict changes in weather patterns by relating the temperature, pressure, and volume of air masses, which helps in forecasting weather.
- Respiratory Physiology: The Ideal Gas Law aids in understanding how gases exchange in the lungs. By relating the pressure and volume of gases, you can predict how oxygen and carbon dioxide will diffuse between the lungs and the bloodstream, which is essential for studying respiratory function and disorders.
- Gas Storage and Transportation: The Ideal Gas Law helps in designing storage and transportation systems for gases. By understanding how pressure and temperature affect gas volume, you can optimize conditions for safe and efficient storage and transport, whether for industrial gases, natural gas, or medical oxygen.
Examples for Ideal Gas Law
- Determining the Volume of a Gas: If you have 1 mole of an ideal gas at standard temperature and pressure (0°C and 1 atmosphere), the gas occupies 22.4 liters. This example shows the consistent volume a mole of gas takes under these conditions, useful in laboratory calculations.
- Calculating Pressure in a Container: If you have a 10-liter container holding 0.5 moles of an ideal gas at 25°C, you can determine the pressure inside the container. This application is vital in scenarios like calculating the pressure in gas cylinders used in various industrial processes.
- Finding the Temperature of a Gas: If you have 2 moles of an ideal gas in a 5-liter container at a pressure of 3 atmospheres, you can calculate the temperature. This example is essential in processes where controlling the temperature is critical, such as chemical reactions.
- Determining the Number of Moles in a Gas Sample: If you have a 15-liter container of gas at 2 atmospheres and 300 K, you can find the number of moles present. This calculation is crucial in determining the quantity of gas needed or produced in industrial applications.
- Real-World Application in Balloons: To fill a balloon with helium so it has a specific volume at room temperature and atmospheric pressure, you can use the Ideal Gas Law to determine the amount of helium required. This application is common in events and scientific experiments involving gases.
- Automotive Applications: Engineers use the Ideal Gas Law to calculate pressure changes in car tires. For instance, if the temperature of a tire increases, the pressure also increases. Understanding this relationship helps in designing safer and more efficient tires.
- Medical Applications: In anesthesiology, the Ideal Gas Law helps calculate the amount of anesthetic gas needed for patients. Knowing the precise volume and pressure ensures the correct dosage and safe administration of gases like nitrous oxide.
- Engineering Applications: Engineers use the Ideal Gas Law in designing and operating equipment such as internal combustion engines and refrigeration systems. This application helps predict how gases will behave under different conditions, ensuring optimal performance.
- Meteorology and Atmospheric Science: The Ideal Gas Law is fundamental in modeling atmospheric processes. Meteorologists use it to predict weather patterns by relating the temperature, pressure, and volume of air masses, aiding in weather forecasting.
- Respiratory Physiology: The Ideal Gas Law aids in understanding gas exchange in the lungs. By relating pressure and volume, it helps predict how oxygen and carbon dioxide will diffuse between the lungs and bloodstream, essential for studying respiratory functions.
FAQ’s
What is the difference between ideal and real gases?
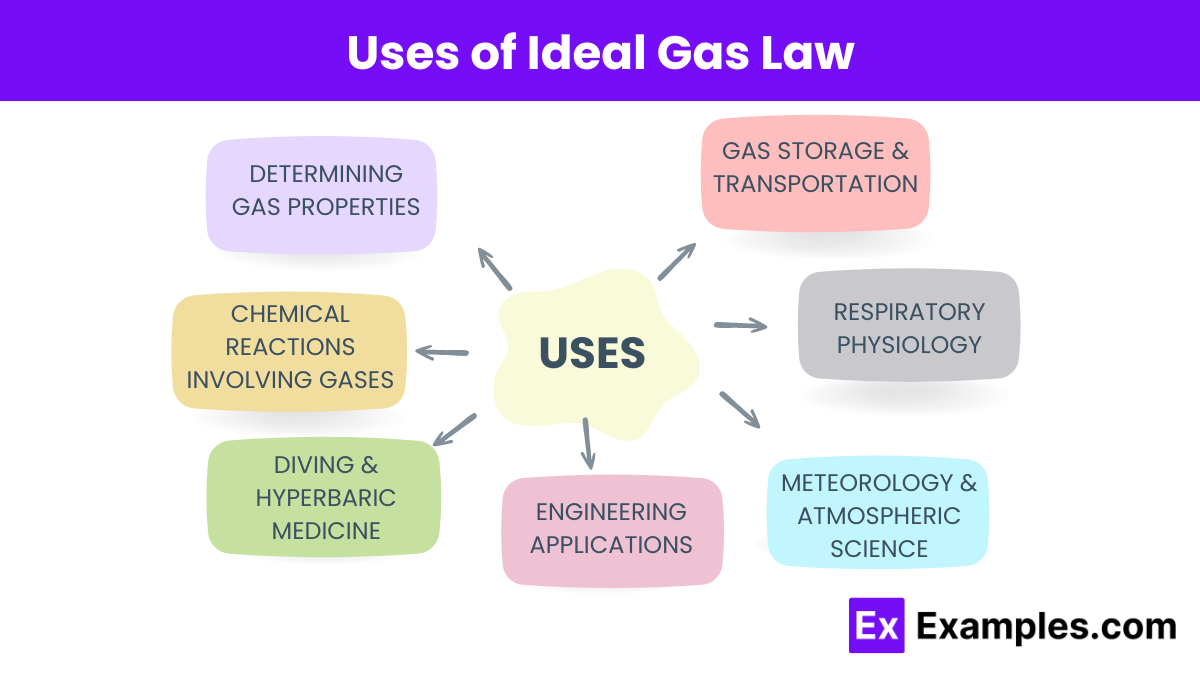
Ideal gases follow the ideal gas law perfectly; real gases deviate due to intermolecular forces and finite molecular volume.
Can the ideal gas law predict gas behavior at all conditions?
No, the ideal gas law predicts gas behavior accurately only under ideal conditions, usually high temperature and low pressure.
What are the assumptions of the ideal gas law?
Assumptions include negligible molecular volume, no intermolecular forces, and perfectly elastic collisions.
How does the ideal gas law apply to chemical reactions?
The ideal gas law helps calculate the amounts of reactants and products in gaseous form, using volume and pressure relationships.
What is the significance of Avogadro’s Law in the ideal gas law?
Avogadro’s Law states that equal volumes of gases, at the same temperature and pressure, have the same number of molecules, represented in the ideal gas law by n.
What is the importance of temperature in the ideal gas law?
Temperature (T) must be in kelvins for accurate calculations since it directly affects gas volume and pressure.
When is the ideal gas law applicable?
The ideal gas law is applicable at high temperature and low pressure, where gases behave ideally.
What do the variables in the ideal gas law represent?
P is pressure, V is volume, n is moles of gas, R is the gas constant, and T is temperature.
What is the value of the gas constant (R)?
The gas constant R is 8.314 J/(mol·K).
How do you use the ideal gas law to find pressure?
Rearrange the ideal gas law to P = nRT/V and plug in the values for n, R, T, and V.
Share :
Practice Test
In the Ideal Gas Law, what does the constant R represent?
Volume
Pressure
Gas constant
Temperature
of 10
If pressure is measured in atmospheres, volume in liters, and temperature in Kelvin, what is the value of R?
8.314 J/(mol K)
0.0821 L atm/(mol K)
1.987 cal/(mol K)
0.8314 L atm/(mol K)
of 10
Which of the following represents the correct units for pressure in the Ideal Gas Law?
Kelvin
Liters
Atmospheres
Moles
of 10
How does the volume of a gas change if the temperature is increased while keeping pressure and moles constant?
Increases
Decreases
Remains constant
Doubles
of 10
If the number of moles of gas is doubled while keeping temperature and volume constant, what happens to the pressure?
Halves
Doubles
Remains the same
Quadruples
of 10
What happens to the pressure of a gas if its volume is halved while keeping temperature and moles constant?
Halves
Doubles
Remains the same
Triples
of 10
If the temperature of a gas is measured in Celsius, what must be done before using the Ideal Gas Law?
Convert to Kelvin
Convert to Fahrenheit
Convert to Rankine
Convert to Reaumur
of 10
What is the value of R when pressure is measured in Pascals, volume in cubic meters, and temperature in Kelvin?
8.314 J/(mol K)
0.0821 L atm/(mol K)
62.36 L torr/(mol K)
1.987 cal/(mol K)
of 10
Which variable is held constant in Charles's Law?
Pressure
Volume
Temperature
Moles
of 10