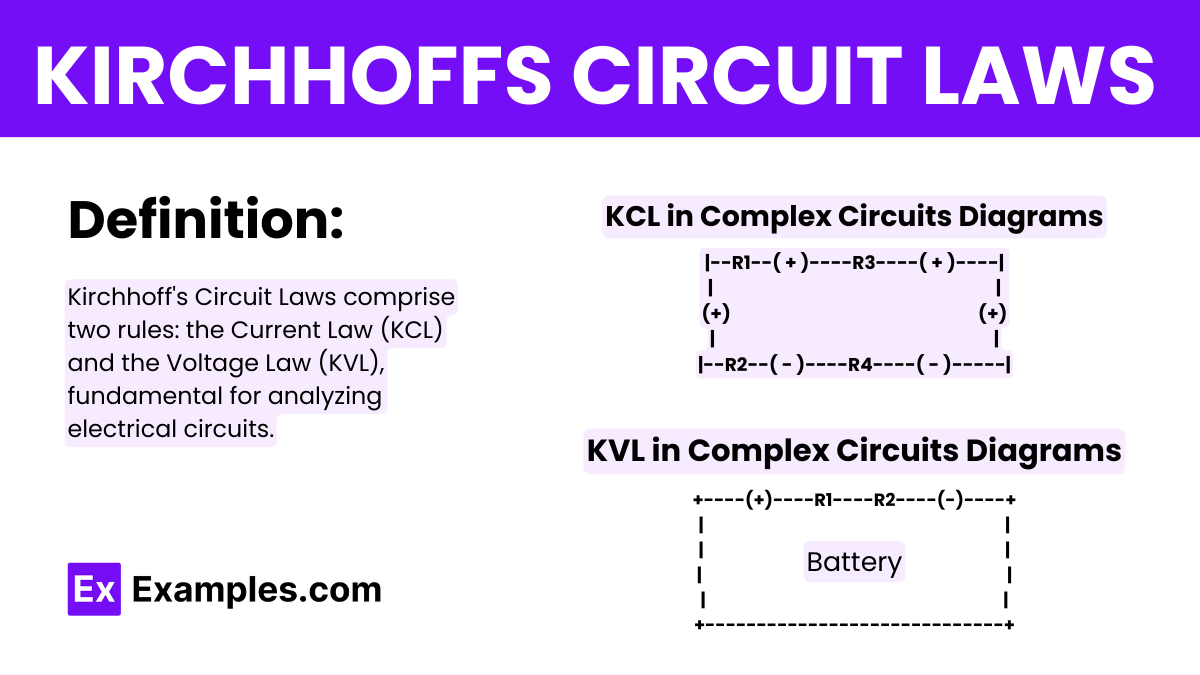
What does Kirchhoff's Voltage Law (KVL) state?
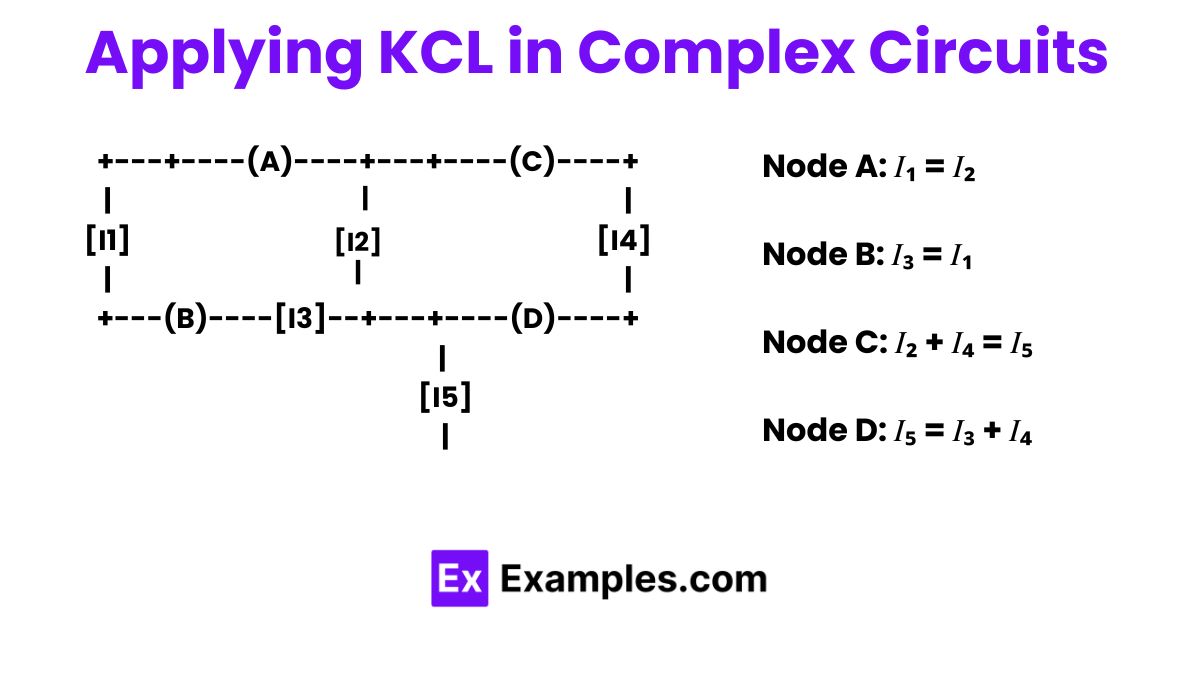
The total current entering a junction equals the total current leaving the junction.
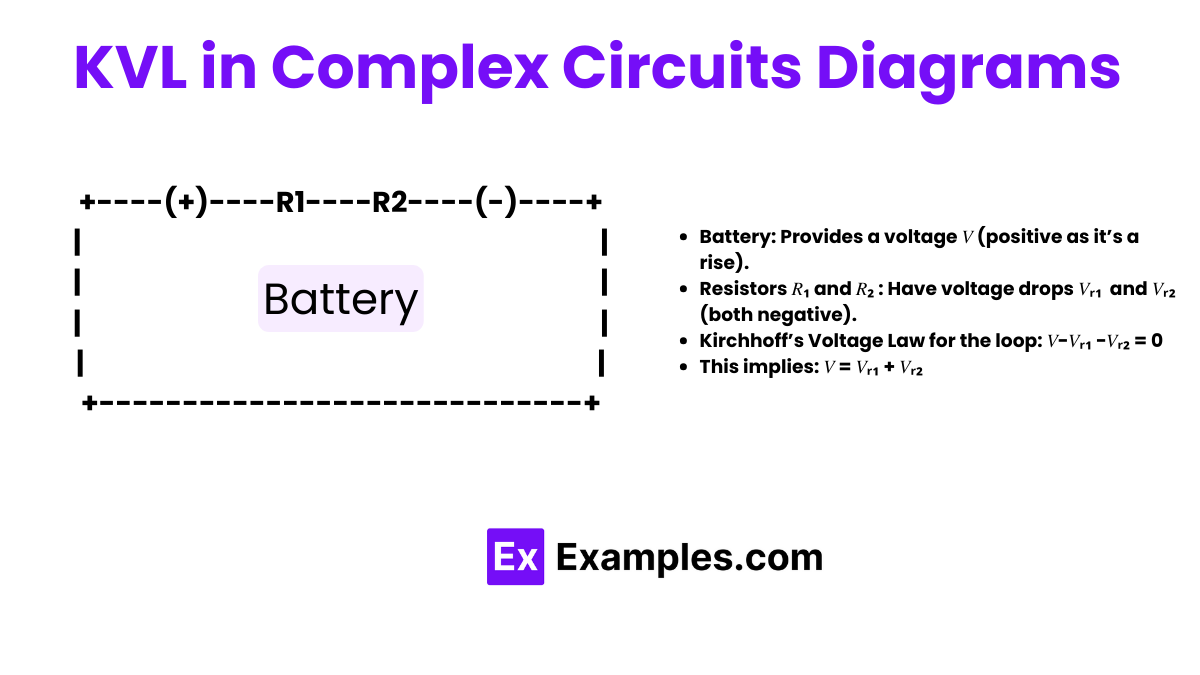
The total voltage around any closed loop in a circuit is zero.
The total resistance in a circuit is equal to the sum of individual resistances.
The total power in a circuit is constant.