Law of Equipartition of Energy

The Law of Equipartition of Energy is a fundamental principle in statistical mechanics. A branch of physics that deals with the behavior of systems with a large number of particles. This law provides crucial insights into how energy is distributed among the degrees of freedom of a system at thermal equilibrium.

What is Law of Equipartition of Energy?

The Law of Equipartition of Energy is a fundamental concept in statistical mechanics, significantly enhancing our understanding of how energy distributes itself among the various degrees of freedom in a system at thermal equilibrium.

Types of Law of Equipartition of Energy

The Law of Equipartition of Energy primarily describes how energy distributes equally among the degrees of freedom in a system at thermal equilibrium. This principle manifests in different contexts, explaining various physical phenomena.

Classical Equipartition Theorem

The classical version of the equipartition theorem states that each degree of freedom that appears quadratically in the energy expression contributes 1/2𝑘𝑇 to the average energy of the system. Where 𝑘 is Boltzmann’s constant, and 𝑇 is the temperature in Kelvin.

Molecular Degrees of Freedom

• Translational Degrees of Freedom: Each molecule in a gas has three translational degrees of freedom. Corresponding to motion along the 𝑥, 𝑦, and 𝑧 axes, each contributing 1/2𝑘𝑇 to the kinetic energy.
• Rotational Degrees of Freedom: Molecules, depending on their shape, can have up to three rotational degrees of freedom (about the three axes), each also contributing 1/2𝑘𝑇 to the rotational kinetic energy.
• Vibrational Degrees of Freedom: For each vibrational mode (oscillations along molecular bonds), there are two degrees of freedom, one for potential energy and one for kinetic energy, contributing a total of 𝑘𝑇 per mode.

Quantum Mechanical Equipartition

In quantum mechanics, quantization of energy levels causes the equipartition theorem to apply differently. The energy distribution among the degrees of freedom depends on the temperature. Relative to the energy quantum of the mode. Thus, the classical equipartition theorem only applies at high temperatures. Where the thermal energy greatly exceeds the quantum of energy for the mode.

Law of Equipartition of Energy Formula

The law states that each degree of freedom that contributes quadratically to the system’s energy receives an average energy of 1/2𝑘𝑇, where:

• 𝑘 is the Boltzmann constant (1.38×10⁻²³ J/K),
• 𝑇 is the absolute temperature in Kelvin.

In general terms, for a system at thermal equilibrium, the total energy 𝐸E is distributed equally across all its degrees of freedom, and the expression becomes:

⟨𝐸⟩=𝑓/2𝑘𝑇

• ⟨𝐸⟩ represents the average total energy of the system,
• 𝑓 denotes the total number of degrees of freedom available to the system.

Law of Equipartition of Energy Derivation

In classical statistical mechanics, we often describe the total energy of a system using the Hamiltonian, which may include various types of energy such as kinetic and potential. We can express the Hamiltonian as a function of the particles’ positions and momenta in the system.

Setting Up the Expression

Consider a system described by the Hamiltonian 𝐻(𝑝,𝑞), where p represents the generalized momenta and q represents the generalized coordinates of the particles in the system. The system is assumed to be at thermal equilibrium, and the particles follow the Maxwell-Boltzmann distribution.

Boltzmann Distribution

The probability 𝑃P that the system is in a particular state with energy E is given by the Boltzmann factor:

𝑃(𝐸)∝𝑒⁻ᴱ/ᴷᵀ

where 𝑘 is the Boltzmann constant and 𝑇 is the temperature of the system.

Integration Over Phase Space

To find the average energy associated with a specific degree of freedom, integrate over all phase space while keeping one variable, say a component of the momentum 𝑝𝑖, fixed:

⟨𝐸⟩=∫𝑝𝑖²/2𝑚𝑒^−𝑝𝑖²/2𝑚𝑘𝑇𝑑𝑝ᵢ​

This integral focuses on the kinetic part of the energy for one degree of freedom associated with the momentum 𝑝𝑖.

The integral simplifies using Gaussian integration techniques, where the average kinetic energy associated with one component of the momentum is:

⟨𝑝𝑖²/2𝑚⟩=1/2𝑘T

This expression states that the average kinetic energy per degree of freedom is 1/2𝑘𝑇.

Extending to All Degrees of Freedom

Since the derivation can be applied to any quadratic degree of freedom (either in kinetic or potential form), each degree of freedom contributes 1/2𝑘𝑇 to the total energy. Therefore, if a system has 𝑓 degrees of freedom, the total energy at equilibrium is:

⟨𝐸⟩=𝑓/2𝑘𝑇

Uses of Law of Equipartition of Energy

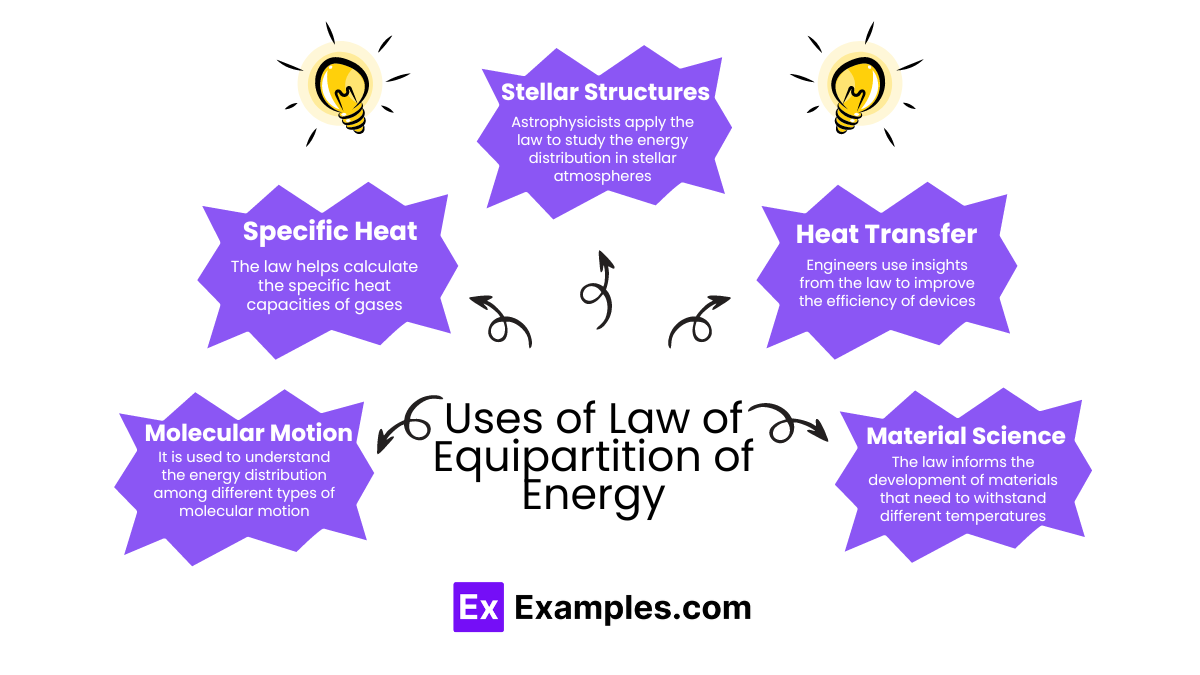
The Law of Equipartition of Energy is fundamental in physics and has broad applications across various scientific fields. Here are some key uses:

• Determining Specific Heat Capacities: The law calculates the specific heat capacities of gases. Predicting how much heat is necessary to raise the temperature of a gas by a certain amount, based on its degrees of freedom.
• Analyzing Molecular Motion: Researchers use it to understand the energy distribution among different types of molecular motion—translational, rotational, and vibrational—in gases. This analysis helps interpret molecular behavior under various thermal conditions.
• Studying Stellar Structures: Astrophysicists apply the law to study the energy distribution in stellar atmospheres and interiors. Aiding models of how stars evolve and behave over time.
• Developing Heat Transfer Technologies: Engineers employ insights from the law to enhance the efficiency of devices that rely on heat transfer. Such as heat exchangers and thermal insulators.
• Enhancing Materials Science: The law guides the development of materials that must withstand different temperatures and pressures. Particularly in the design of aerospace materials and systems.

Examples for Law of Equipartition of Energy

The Law of Equipartition of Energy provides valuable insights across various applications. Here are some specific examples illustrating its utility:

• Temperature Control in Gases: The law explains why gases at the same temperature have the same average kinetic energy, which is crucial for designing HVAC systems and other temperature control technologies.
• Analysis of Heat Capacities: It helps predict the molar specific heats of gases by considering their degrees of freedom, essential for chemical engineering and materials science.
• Astrophysics: The law is used to understand the thermal properties of stars, including energy distribution in stellar interiors and atmospheres, aiding in models of star life cycles and structure.
• Biophysical Applications: In biophysics, the law explains how energy is distributed in the molecular motions of proteins and other biomolecules. Which is key for understanding cellular processes.
• Nanotechnology: Researchers apply the law to study energy distribution at the nanoscale. Influencing the design of nano-devices and materials that operate under various thermal conditions.

FAQ’S

What is the principle of equipartition?

The principle of equipartition states that energy distributes equally among all available degrees of freedom at thermal equilibrium in a system.

What is the equipartition of energy kinetic theory?

In kinetic theory, the equipartition of energy principle explains that each degree of freedom. In a gas molecule contributes equally to its kinetic energy.

Who gave the law of equipartition of energy?

James Clerk Maxwell and Ludwig Boltzmann developed the law of equipartition of energy. Elaborating on how energy equilibrates in thermodynamic systems.