What does the Maxwell-Boltzmann distribution describe?
Distribution of particle speeds in a gas
Distribution of electric charges in a conductor
Distribution of magnetic fields in a material
Distribution of photons in a light beam
of 10
Maxwell Boltzmann Distribution Law – Examples, Definition, FAQ’S
Maxwell Boltzmann Distribution Law – Examples, Definition, FAQ’S
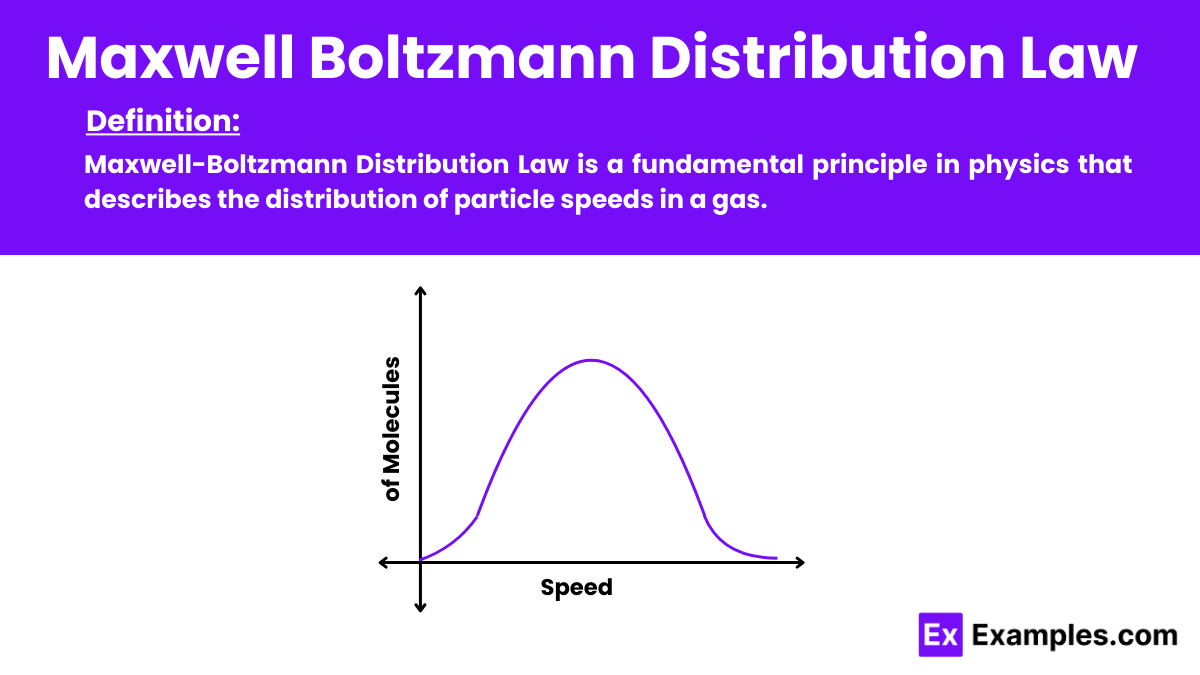
Maxwell-Boltzmann Distribution Law is a fundamental principle in physics that describes the distribution of particle speeds in a gas. This law of physics applies to ideal gases and states that the fraction of particles moving at a specific speed depends on the temperature and the particle’s mass. The distribution curve shows that most particles move at an average speed, with fewer particles moving at much higher or lower speeds. This law is essential in statistical mechanics. Providing insight into the kinetic behavior of gas molecules.
What is Maxwell Boltzmann Distribution Law?
Maxwell Boltzmann Distribution Law Formula
The formula for the Maxwell-Boltzmann Distribution Law describes the distribution of speeds of particles in an ideal gas. It is expressed as:
where:
- 𝑓(𝑣): Probability density function of particle speed 𝑣
- 𝑚: Mass of a gas particle
- 𝑘: Boltzmann constant (1.38×10⁻²³ J/K)
- 𝑇: Absolute temperature (in Kelvin)
- 𝑣: Speed of the gas particle
The formula provides the probability of finding a particle with a particular speed at a given temperature. It shows that the speed distribution is skewed, with most particles having a moderate speed, and fewer particles having very low or very high speeds.
Maxwell Boltzmann Distribution Law Derivation
The Maxwell-Boltzmann Distribution Law provides the statistical distribution of speeds for particles in an ideal gas. Here’s a simplified derivation:
Energy of a Particle: Consider a single gas particle with kinetic energy 𝐸=1/2𝑚𝑣². Where 𝑚 is the particle’s mass and v is its speed.
Distribution of Energies: The probability of finding a particle with a specific energy follows the Boltzmann distribution, which is 𝑃(𝐸)∝𝑒−𝐸𝑘𝑇. Here, 𝑘 is the Boltzmann constant, and 𝑇 is the absolute temperature.
Probability Distribution: Since 𝐸=1/2𝑚𝑣², the speed distribution becomes: 𝑃(𝑣)∝𝑣²𝑒^−𝑚𝑣²/2𝑘𝑇. The 𝑣² term arises because we consider the number of possible states for each energy level.
Normalization: To find the exact distribution, the function must be normalized to integrate to 1 over all possible speeds. This gives the full Maxwell-Boltzmann distribution: 𝑓(𝑣)=4𝜋(𝑚/2𝜋𝑘𝑇)^3/2𝑣²𝑒^−𝑚𝑣²/2𝑘𝑇
This formula describes the probability distribution of speeds for gas particles, showing that most particles have a moderate speed, with fewer particles having very high or very low speeds.
Uses of Maxwell Boltzmann Distribution Law
- Kinetic Theory of Gases: This law provides insight into how gas molecules distribute their speeds, thereby allowing scientists to predict gas behavior at different temperatures.
- Thermodynamics: Physicists use the distribution to understand energy distributions in gases. Which is essential in calculating thermodynamic properties like pressure and temperature.
- Statistical Mechanics: The law plays a key role in understanding the statistical behavior of particles, forming a foundation for the study of gases.
- Chemical Reactions: Chemists utilize the Maxwell-Boltzmann distribution to predict the speed at which reactions occur, as it helps in understanding the collision rates of reacting molecules.
- Transport Phenomena: The law aids in analyzing transport phenomena such as diffusion and viscosity by predicting how particle speeds affect these processes.
- Atmospheric Science: Researchers apply the distribution to model the behavior of gases in the atmosphere, which helps in studying weather patterns and climate change.
Examples for Maxwell Boltzmann Distribution Law
- Gas Behavior in Atmospheres: Researchers study planetary atmospheres to determine the speed distribution of gas molecules. By applying the Maxwell-Boltzmann distribution, they can better predict temperature and pressure variations at different altitudes.
- Chemical Reaction Rates: In chemistry, the law predicts the speed distribution of reacting molecules. As a result, scientists use this information to estimate collision rates, which, in turn, helps in understanding reaction kinetics.
- Thermal Conductivity: By examining the speed distribution of gas particles, engineers utilize the Maxwell-Boltzmann distribution to understand how temperature affects the thermal conductivity of gases and improves heat transfer processes.
- Velocity Distribution in Laboratories: In physics experiments, researchers rely on the Maxwell-Boltzmann distribution to analyze the velocities of gas particles in controlled environments. Thus, they gain insights into the influence of temperature and molecular mass.
- Ideal Gas Studies: Scientists use this law to understand the behavior of ideal gases. Particularly when estimating properties such as internal energy and entropy based on particle speed distributions.
FAQ’S
What affects Maxwell-Boltzmann distribution?
Temperature and particle mass significantly affect the distribution. Increased temperature shifts speeds higher, and lighter particles reach higher speeds than heavier ones.
What is the unit of the Boltzmann distribution?
The Boltzmann distribution is a probability density function, so it has units of 1/speed for the Maxwell-Boltzmann distribution.
How does temperature affect Maxwell Boltzmann distribution?
Higher temperatures broaden the distribution, increasing the average particle speed, while lower temperatures narrow it, reducing particle speed.
Share :
Practice Test
Which of the following is a key assumption of the Maxwell-Boltzmann distribution?
All particles have the same speed
Particles move in random directions
Particles do not collide
Particles have the same mass
of 10
In the context of the Maxwell-Boltzmann distribution, what does the term "most probable speed" refer to?
The average speed of particles
The speed at which the largest number of particles move
The maximum speed of particles
The minimum speed of particles
of 10
How does temperature affect the Maxwell-Boltzmann distribution of particle speeds?
Higher temperature shifts the distribution to higher speeds
Higher temperature shifts the distribution to lower speeds
Temperature has no effect
Higher temperature decreases the number of particles
of 10
What does the area under the Maxwell-Boltzmann distribution curve represent?
Total energy of the system
Total number of particles
Total pressure of the gas
Total volume of the gas
of 10
Which of the following is true about the shape of the Maxwell-Boltzmann distribution curve at very high temperatures?
It becomes narrower
It becomes broader
It becomes flat
It becomes more peaked
of 10
What does the Maxwell-Boltzmann distribution law imply about the kinetic energy of gas particles?
All particles have the same kinetic energy
Kinetic energy is uniformly distributed among particles
Kinetic energy varies and follows a specific distribution
Kinetic energy is inversely proportional to temperature
of 10
Which factor is directly proportional to the average kinetic energy of gas particles in the Maxwell-Boltzmann distribution?
Volume of the gas
Pressure of the gas
Temperature of the gas
Number of particles
of 10
How does the most probable speed compare to the average speed in a Maxwell-Boltzmann distribution?
Most probable speed is higher
Most probable speed is lower
They are equal
Relationship varies with temperature
of 10
What effect does increasing the mass of gas particles have on the Maxwell-Boltzmann distribution?
Shifts the distribution to higher speeds
Shifts the distribution to lower speeds
Broadens the distribution
Narrows the distribution
of 10