Newtons Law of Cooling – Examples, Definition, Derivation, FAQ’S

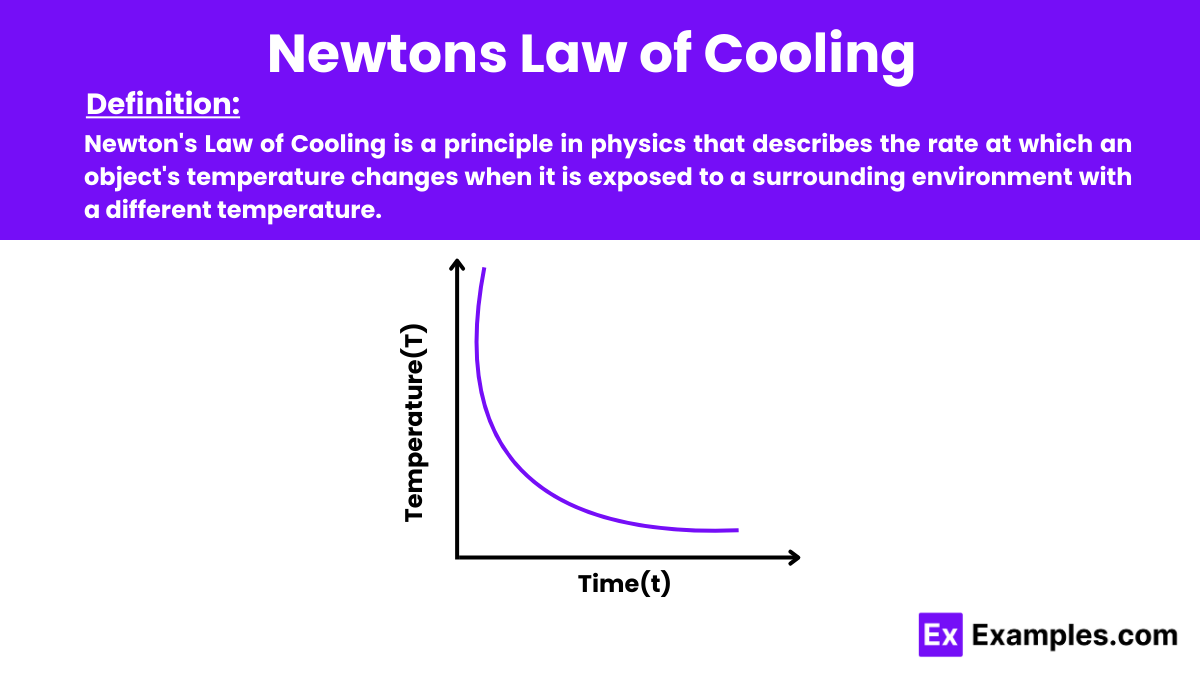
Newton’s Law of Cooling is a principle in physics that describes the rate at which an object’s temperature changes when it is exposed to a surrounding environment with a different temperature. According to this law of physics, the rate of heat loss of a body is proportional to the difference in temperatures between the body and its surroundings. This relationship is crucial in understanding and predicting how quickly an object will reach thermal equilibrium with its environment.

What is Newtons Law of Cooling?

Newtons Law of Cooling Formula

Newton’s Law of Cooling is mathematically expressed by the formula:

where:

• 𝑑𝑇/𝑑𝑡​ is the rate of change of the temperature (𝑇) of the object over time (t),
• 𝑇 is the temperature of the object at time 𝑡,
• 𝑇ₑₙᵥ​ is the constant temperature of the surrounding environment,
• 𝑘 is a positive constant specific to the system, representing the cooling constant or the thermal conductivity of the environment.

This formula shows that the rate at which the temperature of an object approaches the environmental temperature is proportional to the difference between the current temperature of the object and the environmental temperature.

Newtons Law of Cooling Derivation

Newton’s Law of Cooling describes how the temperature of an object changes as it comes into thermal equilibrium with its surroundings. The law states that the rate of heat loss of an object is proportional to the difference in temperature between the object and its surroundings. Here’s a simplified derivation:

Newton’s Law of Cooling assumes that the heat transfer between an object and its surroundings occurs through convection and is proportional to the temperature difference between them.

Heat Transfer Equation: The rate of heat transfer 𝑄 (in watts or joules per second) can be described by the equation: 𝑄=ℎ𝐴(𝑇−𝑇ₑₙᵥ)

Here,

• ℎ is the heat transfer coefficient,
• 𝐴 is the surface area of the object through which heat is being transferred,
• 𝑇 is the temperature of the object,
• 𝑇ₑₙᵥ​ is the temperature of the surrounding environment.

Relating Heat Transfer to Temperature Change: The heat transfer leads to a change in temperature of the object, which can be described by the heat capacity equation: 𝑄=𝑚𝑐𝑑𝑇/𝑑𝑡​

• 𝑚 is the mass of the object,
• 𝑐 is the specific heat capacity of the material,
• 𝑑𝑇/𝑑𝑡​ is the rate of temperature change of the object.

Combining Equations: Equating the heat transfer equations,

we get: 𝑚𝑐𝑑𝑇/𝑑𝑡=ℎ𝐴(𝑇−𝑇ₑₙᵥ)

Simplifying, 𝑑𝑇/𝑑𝑡=ℎ𝐴/𝑚𝑐(𝑇−𝑇ₑₙᵥ)

We define the cooling constant 𝑘 as: 𝑘=ℎ𝐴/𝑚𝑐 Thus, 𝑑𝑇/𝑑𝑡=−𝑘(𝑇−𝑇ₑₙᵥ)

The negative sign indicates that the temperature 𝑇 of the object decreases over time if it is higher than 𝑇ₑₙᵥ​.

Exponential Decay Form: This differential equation can be solved to give: 𝑇(𝑡)=𝑇ₑₙᵥ+(𝑇₀−𝑇ₑₙᵥ)𝑒^−𝑘𝑡

Here, 𝑇₀​ is the initial temperature of the object at 𝑡=0.

This derivation shows that the temperature of an object exponentially approaches the ambient temperature, with the rate of cooling being dependent on the properties of the object and its environment. This formula is widely used in various scientific and engineering applications where cooling is involved.

Methods to Apply Newton’s Law of Cooling

Measuring Temperature Decay

• Measure the initial temperature of a hot object and its surrounding environment.
• Monitor the object’s temperature over time at regular intervals.
• Use Newton’s Law of Cooling to calculate the rate of temperature decay and predict future temperatures.

Calibrating Thermometers

• Place the thermometer in a controlled environment with a stable temperature.
• Use an object with a known cooling rate to compare how the thermometer reads temperatures as it cools down. Apply Newton’s Law of Cooling to adjust the thermometer’s readings for accurate calibration.

Estimating Cooling Time

• Record the starting temperature of a hot object and the surrounding ambient temperature.
• Apply the formula given by Newton’s Law of Cooling to estimate how long it will take for the object to cool to a specific temperature.

Forensic Time-of-Death

• Measure the body temperature of a deceased person and note the ambient temperature. Apply Newton’s Law of Cooling to estimate how much time has passed since the body stopped producing heat.

Uses of Newtons Law of Cooling

1. Food Safety and Preservation: In the food industry, managers use Newton’s Law of Cooling to estimate how long cooked food will take to reach safe storage temperatures. As a result, they can prevent bacterial growth and ensure safe consumption.
2. Forensic Time-of-Death Estimation: Medical examiners apply this law to estimate the time of death. By comparing a body’s temperature with the ambient temperature, they can approximate how long it’s been since the body ceased to produce heat.
3. Cooling System Design: Engineers use Newton’s Law to design efficient cooling systems. By predicting the rate of heat loss from heated objects, they can develop systems that maintain optimal temperatures for equipment and processes.
4. Calibrating Thermometers: Technicians rely on Newton’s Law of Cooling to calibrate thermometers. They compare temperature readings over time against known cooling rates, ensuring accurate measurements.
5. Meteorology: Meteorologists use this principle to predict how temperatures will change overnight. By understanding the heat loss rate, they can forecast how quickly the environment will cool once the sun sets.
6. Material Testing: In material testing, Newton’s Law helps determine the thermal properties of various materials.

Examples for Newtons Law of Cooling

1. Cooling Hot Coffee: When you pour hot coffee into a mug and leave it on a table, the coffee gradually cools down as it releases heat into the surrounding air. You can predict how long it will take for the coffee to reach a drinkable temperature by applying Newton’s Law of Cooling.
2. Boiling Water Cooling Off: After boiling water on the stove, the pot gradually cools to room temperature. The water cools faster initially when its temperature is much higher than the ambient air. Over time, as the temperature difference decreases, the cooling rate slows down, illustrating Newton’s Law of Cooling.
3. Body Temperature Post-Exercise: Your body temperature rises during intense exercise and gradually returns to normal afterward. Newton’s Law of Cooling can predict how quickly your body cools down based on the temperature difference between your skin and the surrounding air. The greater this difference, the faster your body will release heat.
4. Hot Metal Cooling in Air: When blacksmiths or metalworkers heat metal and then let it cool in the air, the metal’s temperature initially drops quickly before slowing down as the temperature difference diminishes. Newton’s Law of Cooling provides an accurate prediction of this temperature drop over time.
5. Cooling of Baked Goods: Freshly baked bread or cookies are placed on a rack to cool. Initially, the temperature drops rapidly due to the high difference between the baked goods and the kitchen air. As the temperature gap closes, the cooling rate slows down, following Newton’s Law of Cooling.
6. Industrial Heat Treatment: In manufacturing, metal parts often undergo heat treatment for strength and durability. After heating, the parts cool down to room temperature, and Newton’s Law of Cooling helps predict this cooling rate, ensuring that the treatment meets required specifications.

FAQ’S

How to verify Newton’s law of cooling?

Measure the temperature of a hot object over time as it cools. Plot the data, and observe if the rate of temperature change matches the predicted exponential decay.

Is Newton’s law of cooling linear?

No, it is not linear. Newton’s Law of Cooling follows an exponential relationship, where the rate of temperature change decreases as the difference between the object and ambient temperature narrows.

Does Newton’s law of cooling apply to warming?

Yes, it applies to warming. The law works symmetrically, describing how an object’s temperature approaches the surrounding environment whether it’s cooling or warming up.