What is the center of mass of a system of particles?
The point where the total mass of the system is concentrated
The point where gravitational force acts
The point where external forces are zero
The geometric center of the system
of 10
System of Particles and Rotational Dynamics – 10+ Examples, Applications
System of Particles and Rotational Dynamics – 10+ Examples, Applications
System of Particles and Rotational Dynamics involves the study of the motion of systems consisting of multiple particles and the rotation of rigid bodies. In this domain, we analyze the center of mass, which represents the average position of all the mass in a system, and examine how forces and torques affect the motion of the entire system. Understanding rotational dynamics requires comprehending angular displacement, velocity, and acceleration, as well as the moment of inertia, which quantifies the distribution of mass around an axis of rotation. Key principles such as the law of conservation of angular momentum and Newton’s laws for rotation play a crucial role in predicting and explaining rotational motion in physical systems.
What is System of Particles and Rotational Dynamics?
System of Particles and Rotational Dynamics is a branch of classical mechanics that examines the motion and equilibrium of systems made up of multiple particles. It focuses on how forces affect the collective motion, considering individual masses and positions, and explores rotational motion around a common axis. Key concepts include torque, angular momentum, and rotational kinematics, essential for understanding the behavior of complex systems.
Examples of System of Particles and Rotational Dynamics
1. Center of Mass of a Two-Particle System
Two particles with masses 3 kg and 5 kg are positioned at (2, 4) m and (6, 8) m, respectively. The center of mass is calculated as:
R= (3×2+5×6)/3+5, (3×4+5×8)/3+5= (4.5,6.5)m
2. Torque on a Rotating Door
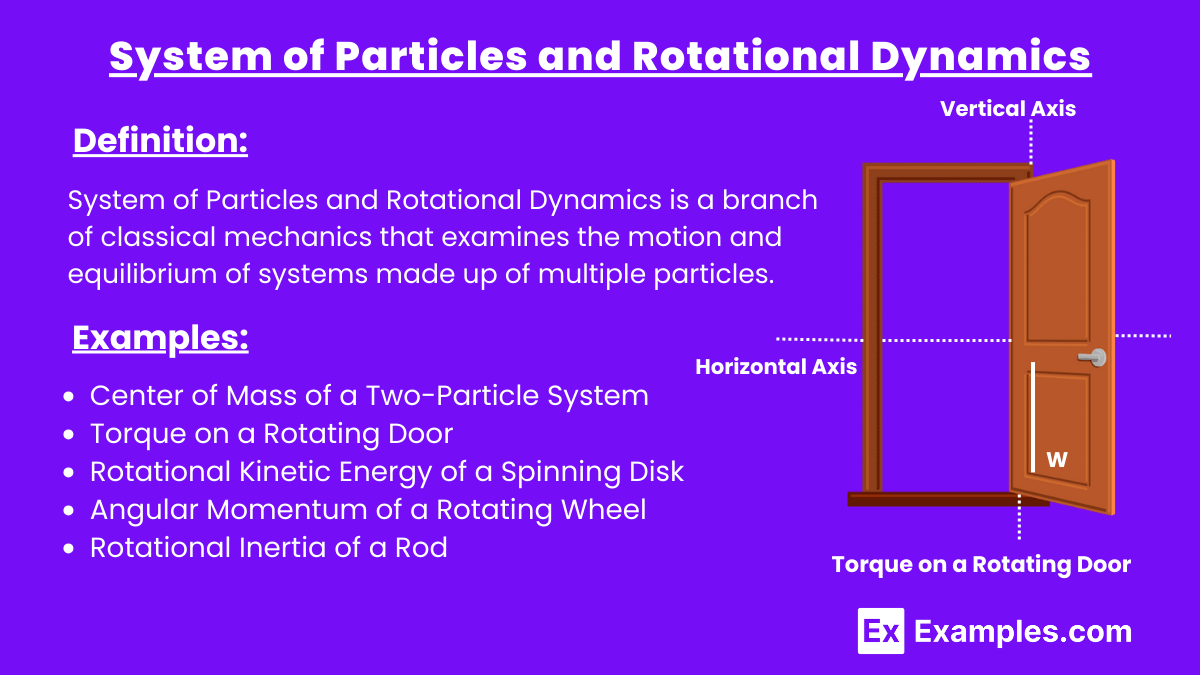
A 15 N force is applied perpendicular to a door at a distance of 1.2 meters from the hinge. The torque is:
τ=1.2m×15N=18Nm
3. Rotational Kinetic Energy of a Spinning Disk
A disk with mass 4 kg and radius 0.3 m spins at 20 rad/s. Its rotational kinetic energy is:
Krot=1/2 × 0.5 × 4 × (0.3)2 × 202=36J
4. Angular Momentum of a Rotating Wheel
A wheel with a moment of inertia of 0.8 kg·m² rotates at 10 rad/s. Its angular momentum is:
L = 0.8kg⋅m2 ×10rad/s = 8kg⋅m2/s
5. Conservation of Angular Momentum in a Diver
A diver tucks into a ball, reducing her moment of inertia from 2 kg·m² to 1 kg·m², doubling her angular velocity from 2 rad/s to:
ω = 2×2/1 = 4rad/s
6. Rotational Inertia of a Rod
A rod with mass 3 kg and length 2 m rotates about its end. The moment of inertia is:
I =1/3 × 3 × 22= 4kg⋅m2
7. Gyroscopic Stability of a Bicycle Wheel
A bicycle wheel spinning at high speed remains stable due to its angular momentum, resisting changes in orientation.
8. Moment of Inertia of a Solid Sphere
A solid sphere with mass 5 kg and radius 0.4 m has a moment of inertia of:
I = 2​/5 × 5 × (0.4)2 = 0.32kg⋅m2
9. Rotational Dynamics of a Merry-Go-Round
A merry-go-round with a moment of inertia of 300 kg·m² accelerates from rest to 2 rad/s under a torque of 100 Nm. The angular acceleration is:
α =100/300 =1/3 rad/s2
10. Angular Acceleration of a Spinning Top
A top with a moment of inertia of 0.02 kg·m² experiences a torque of 0.1 Nm. Its angular acceleration is:
α = 0.1/0.02 =5rad/s2
11. Precession of a Gyroscope
A gyroscope precesses around the vertical axis due to the torque caused by gravity acting on its center of mass, demonstrating the conservation of angular momentum.
12. Rotational Energy of a Hollow Cylinder
A hollow cylinder with mass 6 kg, radius 0.5 m, and angular velocity 15 rad/s has a rotational kinetic energy of:
Krot = 21 ​× 6 × (0.5)2×152=168.75J
Center of Mass
The center of mass is the point in a system of particles or a body where the total mass can be considered to be concentrated. It is the weighted average location of all the mass in the object. This concept is crucial in understanding the motion of objects and systems in physics. Understanding the center of mass helps in analyzing the motion of objects, determining balance and stability, and understanding rotational dynamics. For a system of particles, the center of mass (COM) is calculated using the formula:
- Where:
- mi= mass of the ith particle
- ri= position vector of the ith particle
Linear Momentum of a System
Linear momentum is a fundamental concept in physics, particularly in the study of mechanics. Understanding the linear momentum of a system is crucial for analyzing the motion and interactions of objects. Linear momentum (p) of an object is defined as the product of its mass (m) and its velocity (v):
Torque and Angular Momentum
Torque
Torque (Ï„) is a measure of the rotational force acting on an object. It is defined as the cross product of the position vector (r) and the force vector (F):
Angular Momentum
Angular momentum (L) is a measure of the rotational momentum of an object. For a particle, it is defined as the cross product of the position vector (r) and the linear momentum vector (p):
Applications System of Particles and Rotational Dynamics
System of Particles and Rotational Dynamics are crucial concepts in physics with numerous applications in both everyday life and advanced technology. Here are some key applications:
- Bridges and Buildings: Engineers use the principles of rotational dynamics to ensure the stability of structures. They analyze torque, moments of inertia, and center of mass to prevent collapse.
- Cranes and Lifts: The design of cranes and elevators relies on the balance of forces and torques to lift and move heavy loads safely.
- Automobiles: The stability and handling of cars depend on the distribution of mass and the moments of inertia. Engineers design vehicles to optimize these factors for better performance and safety.
- Bicycles and Motorcycles: The gyroscopic effect, a result of rotational dynamics, helps maintain balance and stability during motion.
- Gymnastics: Gymnasts perform flips and spins by manipulating their moments of inertia, changing their body shape to rotate faster or slower.
- Diving and Skating: Divers and skaters use the principles of rotational dynamics to control their spin rate by tucking in or spreading out their limbs.
- Soccer and Basketball: Players use spin to control the trajectory and stability of the ball. Understanding the rotational motion helps in better aiming and scoring.
- Attitude Control: Satellites and spacecraft use reaction wheels and gyroscopes to control their orientation in space, relying on the principles of rotational dynamics.
- Stabilization: Gyroscopic stabilization keeps spacecraft and satellites oriented correctly without expending fuel.
- Orbital Mechanics: The rotation of celestial bodies and their moments of inertia influence their orbits and rotations, crucial for predicting planetary positions and spacecraft trajectories.
- Washing Machines: The spin cycle in washing machines uses rotational dynamics to remove water from clothes.
- Fans and Mixers: The design and efficiency of fans, mixers, and other rotating appliances depend on understanding rotational motion.
- Tops and Gyroscopes: These toys operate on the principles of rotational dynamics, demonstrating gyroscopic stability and precession.
- Prosthetics and Orthotics: The design of prosthetic limbs and orthotic devices uses principles of rotational dynamics to mimic natural movement and ensure comfort.
- Rehabilitation: Understanding body mechanics and rotational motion helps in designing effective rehabilitation programs for patients with mobility issues.
FAQ’s
What is rotational motion?
Rotational motion occurs when an object spins around an internal axis, like a wheel turning around its axle.
What is torque?
Torque is the measure of the force that causes an object to rotate about an axis. It is the rotational equivalent of force.
What is the moment of inertia?
The moment of inertia quantifies the resistance of an object to changes in its rotational motion about an axis.
How does torque affect rotational motion?
Torque causes angular acceleration in an object, changing its rotational motion based on the object’s moment of inertia.
What is angular momentum?
Angular momentum is the rotational equivalent of linear momentum, describing the quantity of rotation of an object.
What is the principle of conservation of angular momentum?
The principle states that if no external torque acts on a system, its total angular momentum remains constant.
What is a rigid body?
A rigid body is an object with a fixed shape and size that doesn’t deform under the action of forces.
What is the parallel axis theorem?
The parallel axis theorem states that the moment of inertia about any axis parallel to an axis through the center of mass is I+Md2.
What is the perpendicular axis theorem?
The perpendicular axis theorem applies to planar objects, stating that the moment of inertia about an axis perpendicular to the plane is the sum of moments of inertia about two perpendicular axes in the plane.
What is the angular acceleration?
Angular acceleration is the rate of change of angular velocity over time, usually measured in radians per second squared.
Share :
Practice Test
What does the moment of inertia depend on?
Mass only
Distribution of mass and axis of rotation
Shape only
Velocity of rotation
of 10
What is the relationship between torque and angular acceleration in rotational dynamics?
Torque is inversely proportional to angular acceleration
Torque is directly proportional to angular acceleration
Torque is equal to the moment of inertia
Torque does not affect angular acceleration
of 10
Which of the following quantities is conserved in the absence of external torques?
Linear momentum
Angular momentum
Force
Kinetic energy
of 10
What is the effect of increasing the distance of mass from the axis of rotation on the moment of inertia?
It decreases the moment of inertia
It increases the moment of inertia
It has no effect on the moment of inertia
It makes the moment of inertia zero
of 10
Which law explains the rotational analog of Newton's first law?
Law of Conservation of Mass
Law of Inertia
Law of Conservation of Momentum
Law of Universal Gravitation
of 10
How is the angular velocity defined in rotational motion?
The rate of change of angular displacement
The rate of change of linear displacement
The total angle covered
The rate of change of mass
of 10
If a disk and a ring have the same mass and radius, which has a larger moment of inertia about the central axis?
Disk
Ring
Both have the same moment of inertia
It depends on the material
of 10
What does the angular momentum of a system depend on?
Force and time
Mass and velocity
Moment of inertia and angular velocity
Displacement and acceleration
of 10
What happens to the angular velocity if the moment of inertia of a rotating body is halved while keeping the angular momentum constant?
Angular velocity doubles
Angular velocity halves
Angular velocity remains constant
Angular velocity becomes zero
of 10