What does De Broglie's equation describe?
The frequency of electromagnetic waves
The wavelength of particles
The speed of sound waves
The intensity of light

Matter exhibits both particle and wave characteristics. In the 1920s, physicist Louis de Broglie introduced the groundbreaking idea that, just as light demonstrates both wave-like and particle-like properties, matter should also possess a wave nature. This concept, initially hard to grasp, forms a cornerstone of quantum mechanics. This article explores the fascinating wave nature of matter and delves into how this duality shapes our understanding of the physical world.
The de Broglie equation is a fundamental principle in quantum mechanics that describes the wave-like behavior of particles. Proposed by the French physicist Louis de Broglie in 1924, this equation bridges the gap between classical and quantum physics by attributing a wavelength to a particle with momentum.
The de Broglie equation is expressed as:
𝜆 = ℎ/𝑝
where:
The wave nature of matter is a fundamental concept in quantum mechanics introduced by Louis de Broglie in 1924. De Broglie proposed that particles, such as electrons, exhibit wave-like properties, similar to light. This revolutionary idea, known as wave-particle duality, is expressed through De Broglie’s equation: [λ = h/p ] where (λ ) is the wavelength, ( h ) is Planck’s constant, and ( p ) is the momentum of the particle.
This dual nature of particles was confirmed through experiments, such as electron diffraction, which demonstrated that electrons create interference patterns akin to waves. This concept is crucial for the development of quantum mechanics, influencing key principles such as the Schrödinger equation and the Heisenberg uncertainty principle.
Applications of this concept include electron microscopy, which utilizes electron wave properties to achieve higher resolution imaging, and quantum computing, which relies on the wave nature of particles for the development of quantum bits and computing processes. Understanding the wave nature of matter has profoundly transformed our comprehension of the microscopic world, bridging classical and quantum physics and leading to numerous technological advancements.
The Heisenberg Uncertainty Principle is a fundamental concept in quantum mechanics formulated by Werner Heisenberg in 1927. It states that there are intrinsic limits to the precision with which certain pairs of physical properties, known as complementary variables, can be simultaneously known. The most commonly discussed pair is position and momentum.
The uncertainty principle is mathematically expressed as:
Δ𝑥⋅ Δ𝑝 ≥ ℎ/4𝜋
where:
Heisenberg’s Uncertainty Principle is a fundamental concept in quantum mechanics that quantifies the limitations on simultaneously measuring certain pairs of complementary properties of a particle, such as position and momentum. The principle is mathematically expressed through Heisenberg’s Uncertainty Equation.
The uncertainty principle for position and momentum is given by:
Δ𝑥⋅ Δ𝑝 ≥ ℏ/2
The wave nature of matter is a groundbreaking concept in physics. While a particle is localized, a wave is spread out in space. The nature of light depends on our observation: it behaves as a wave in phenomena like interference and diffraction, and as a particle in the photoelectric effect. Light’s dual nature, exhibiting both wave and particle characteristics, led Louis de Broglie to propose that all particles have wave properties. His hypothesis was confirmed by experiments like the Davisson-Germer experiment, demonstrating that particles such as electrons exhibit wave-like behavior, fundamentally altering our understanding of the quantum world.
De Broglie’s hypothesis, proposed by Louis de Broglie in 1924, revolutionized quantum mechanics by suggesting that particles, such as electrons, exhibit wave-like properties. He introduced the concept of wave-particle duality, positing that any moving particle has an associated wavelength. This groundbreaking idea fundamentally changed our understanding of the quantum world, implying that not only light but also matter has both particle and wave characteristics. The hypothesis was confirmed by experiments like the Davisson-Germer experiment, which demonstrated electron diffraction, providing strong evidence for the wave nature of particles.
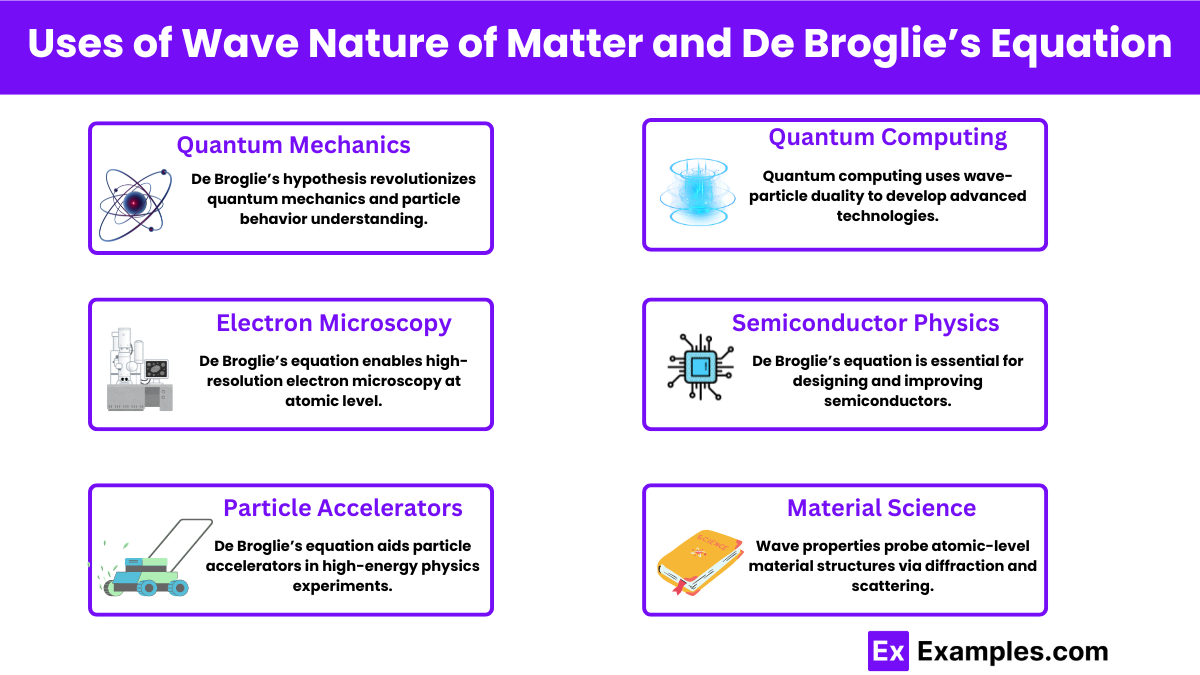
The wave nature of matter and De Broglie’s equation have profound implications in various fields of science and technology. Here are some key uses:
Quantum Mechanics : De Broglie’s hypothesis laid the foundation for quantum mechanics, transforming our understanding of the microscopic world. It explains the behavior of particles at atomic and subatomic scales, influencing key principles such as the Schrödinger equation and the Heisenberg uncertainty principle.
Electron Microscopy : The wave nature of electrons, described by De Broglie’s equation, is utilized in electron microscopes. These microscopes achieve higher resolution images than traditional optical microscopes because the wavelength of electrons is much shorter than that of visible light, allowing scientists to observe structures at the atomic level.
Particle Accelerators : De Broglie’s equation is fundamental in designing and operating particle accelerators. Understanding the wave properties of particles helps in focusing and controlling particle beams, which are used in high-energy physics experiments to explore fundamental particles and forces.
Quantum Computing : Quantum computing relies on the principles of superposition and entanglement, which arise from the wave nature of particles. De Broglie’s equation helps in understanding and manipulating qubits, the basic units of quantum information, enabling the development of powerful computational technologies.
Crystallography : The wave nature of electrons and X-rays is essential in crystallography, a technique used to determine the atomic structure of crystals. By analyzing the diffraction patterns produced when waves pass through a crystal, scientists can infer the arrangement of atoms within the material.
Semiconductor Physics : De Broglie’s equation is crucial in understanding the behavior of electrons in semiconductors. This understanding is essential for designing and improving electronic devices such as transistors, diodes, and integrated circuits, which form the backbone of modern electronics.
Material Science : The wave properties of particles are used to probe and study the properties of materials at the atomic level. Techniques such as electron diffraction and neutron scattering provide insights into the structural, magnetic, and dynamic properties of materials.
Chemistry : In chemistry, the wave nature of electrons is fundamental to understanding chemical bonds and reactions. Quantum mechanics, grounded in De Broglie’s hypothesis, explains how electrons interact within atoms and molecules, leading to the formation of different chemical compounds.
Nuclear Physics : De Broglie’s equation is instrumental in nuclear physics, helping to understand the behavior of particles within an atomic nucleus. It aids in predicting nuclear reactions and properties, which are essential for applications such as nuclear energy and medical imaging.
Astrophysics : In astrophysics, the wave nature of matter helps in understanding phenomena such as the behavior of particles in stars and the formation of black holes. Quantum mechanics, underpinned by De Broglie’s hypothesis, provides insights into the fundamental processes that govern the universe.
The wave nature of matter and De Broglie’s equation have been experimentally validated and applied in various contexts. Here are some key examples:
Electron Diffraction : In 1927, the Davisson-Germer experiment demonstrated electron diffraction, confirming De Broglie’s hypothesis. When a beam of electrons was directed at a crystal of nickel, the resulting diffraction pattern was similar to that of X-rays, which are known to exhibit wave behavior. This experiment provided direct evidence that electrons exhibit wave-like properties.
Double-Slit Experiment : When electrons pass through a double-slit apparatus, they create an interference pattern on a detection screen, much like waves do. This phenomenon demonstrates the wave nature of electrons. However, if the electrons are observed as they pass through the slits, they behave like particles, highlighting the dual nature of matter.
Electron Microscopy : Electron microscopes use the wave nature of electrons to achieve high-resolution imaging. Since electrons have much shorter wavelengths than visible light, they can reveal finer details of a sample, such as the arrangement of atoms in a crystal. This application is crucial in fields like materials science, biology, and nanotechnology.
Neutron Diffraction : Neutron diffraction is a technique used to determine the atomic and/or magnetic structure of a material. Neutrons, which also exhibit wave-like properties, are scattered by the nuclei in a sample. The resulting diffraction pattern provides detailed information about the positions of atoms and their magnetic moments.
Scanning Tunneling Microscopy (STM) : STM relies on the quantum tunneling of electrons between a sharp tip and a sample surface. The wave nature of electrons allows them to tunnel through the potential barrier, enabling the microscope to achieve atomic-scale resolution. This technique is used to visualize and manipulate individual atoms on surfaces.
Quantum Mechanics of Atoms and Molecules : The wave nature of electrons is fundamental to understanding the behavior of electrons in atoms and molecules. Quantum mechanics, which incorporates De Broglie’s hypothesis, explains how electrons form standing waves around nuclei, leading to the formation of atomic orbitals and chemical bonds.
Wave Function and Schrödinger Equation : The wave nature of particles is described by wave functions in quantum mechanics. The Schrödinger equation, which governs the behavior of these wave functions, relies on De Broglie’s hypothesis. This equation predicts how the wave function evolves over time, providing a probabilistic description of a particle’s position and momentum.
Crystal Structure Analysis : X-ray crystallography and electron diffraction are used to determine the crystal structure of materials. The wave nature of X-rays and electrons allows them to produce diffraction patterns when interacting with a crystal lattice. Analyzing these patterns reveals the arrangement of atoms within the crystal.
Quantum Tunneling in Semiconductors : The wave nature of electrons enables quantum tunneling, where electrons can pass through potential barriers that they classically shouldn’t be able to cross. This phenomenon is crucial for the operation of semiconductor devices like tunnel diodes and transistors in modern electronics.
Matter-Wave Interferometry : Matter-wave interferometry uses the wave nature of atoms and molecules to measure small changes in displacement, velocity, and acceleration with high precision. This technique is used in applications ranging from precision measurements in fundamental physics to inertial navigation systems.
De Broglie’s hypothesis was confirmed through experiments such as the Davisson-Germer experiment, which demonstrated electron diffraction.
De Broglie’s equation is fundamental in quantum mechanics as it introduced the concept of wave-particle duality and laid the groundwork for the development of quantum theory.
The Davisson-Germer experiment, conducted in 1927, demonstrated that electrons exhibit diffraction patterns, providing direct evidence of their wave-like nature.
An electron microscope is a type of microscope that uses electrons instead of light to achieve much higher resolution imaging, exploiting the wave nature of electrons.
The wave nature of electrons explains the formation of atomic orbitals, where electrons exist as standing waves around the nucleus, determining chemical properties and bonding.
A wave function is a mathematical description of the quantum state of a particle, encapsulating its wave-like properties and providing probabilities of finding the particle in various positions.
Electron diffraction is a phenomenon where electrons exhibit wave-like behavior, creating interference patterns when passed through a crystal or double slits, similar to light waves.
In electron microscopy, De Broglie’s equation helps determine the wavelength of electrons, enabling high-resolution imaging by utilizing their shorter wavelengths compared to visible light.
Quantum tunneling is a phenomenon where particles pass through a potential barrier that they classically shouldn’t be able to cross, enabled by their wave-like properties
Wave-particle duality is the principle that particles exhibit both wave-like and particle-like properties, depending on the experimental conditions.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What does De Broglie's equation describe?
The frequency of electromagnetic waves
The wavelength of particles
The speed of sound waves
The intensity of light
Which equation represents De Broglie's wavelength of a particle?
λ = h / p
λ = p / h
λ = m / v
λ = c / v
The De Broglie wavelength of a particle increases when:
The mass of the particle increases
The particle's velocity increases
The momentum of the particle increases
The particle's velocity decreases
In which of the following scenarios would a particle exhibit significant wave-like properties?
A baseball in flight
An electron in an atom
A moving car
A falling leaf
Which of the following is the correct unit for De Broglie's wavelength?
Joules
Meters
Kilograms
Seconds
For a particle with very high momentum, its De Broglie wavelength is:
Very long
Very short
Equal to the speed of light
Constant
According to the wave-particle duality, which property of particles can be described by a wave function?
Position
Speed
Mass
Energy
The De Broglie hypothesis suggests that particles have both:
Electric and magnetic properties
Wave and particle properties
Kinetic and potential energy
Temperature and pressure
If the velocity of a particle is doubled, its De Broglie wavelength will:
Be doubled
Be halved
Stay the same
Be quadrupled
What is the primary limitation of observing the wave nature of macroscopic objects?
Their high velocity
Their large mass
Their small size
Their low temperature
Before you leave, take our quick quiz to enhance your learning!

